拉格朗日乘数法

拉格朗日乘数法

通常我们求函数极值的时候，通常我们会求导，并求出导函数等于(0)时变量的取值，例如求一下函数的极值：

[f(x)=x^2+x ]

求导得：

[f'(x)=2x+1 ]

使(f'(x)=0)

[f'(x)=2x+1=0 ]

[x=-frac{1}{2} ]

所以当(x=-frac{1}{2})时，(f(x))有最值。

但如果在约束条件下求最值呢？

例如在双曲线(xy=3)上找出距离原点最近的点。
目标函数为(f(x, y)=sqrt {x^2+y^2})，约束条件为(g(x, y)=xy=3)
注意：这两个函数的变量之间是不独立的，也就是说他们之间存在某种关系，从而限制了各变量的取值，例如这里的函数(g=3)就限制了各变量的取值
我们现在要求(f)的最小值，因为(x^2+y^2)恒非负，所以我们可以求(f(x, y)=x^2+y^2)的最小值。

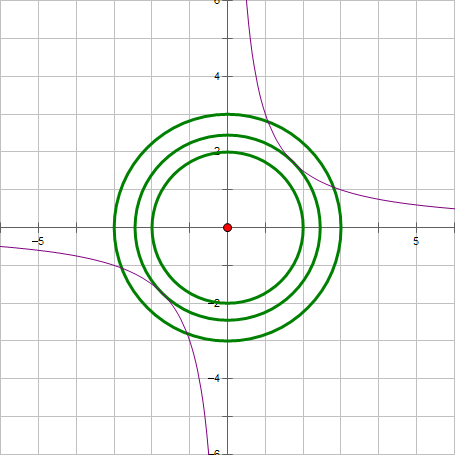
当(f)取不同的值时，与(g)会有不同的交点，或者没有交点。当(f)与(g)相切时，(f)就能取最小值。看其中一个交点

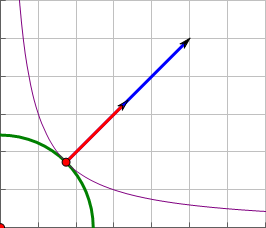
因为(f)与(g)相切，所以他们的法向量是互相平行的，在这些法向量中，其中一个就是函数在该点的梯度。在这里，蓝色为(f)在该点的梯度，红色为(g)在该点的梯度。

[ecause riangledown f parallel riangledown g ]

[ herefore riangledown f= lambda riangledown g ]

[ herefore frac{partial f}{partial x}=lambda frac{partial g}{partial x} ]

[frac{partial f}{partial y}=lambda frac{partial g}{partial y} ]

即

[2x=lambda y ]

[2y=lambda x ]

结合约束条件(xy=3)
解得((-sqrt{3}, -sqrt{3}),(sqrt{3}, sqrt{3}))
((lambda)可以为负，只是这里正好(lambda)为负是无解而已)

这种方法具有一般性吗？

证明：
举三个变量的例子。在(g=c)这一水平集上（我不知道为什么称为水平集，因为它并不水平，只是表示(g=c)这一曲面）的一动点(P)，当(P)保持横坐标不变时， (frac{partial f}{partial x})也是不变的，那么当(frac{partial f}{partial y}=0)时， 该点就是这一曲线上的最值，如果我们把极值连成一曲线，再求导数（即(frac{partial f}{partial x})）为(0)的点，不就是曲面的极值吗？

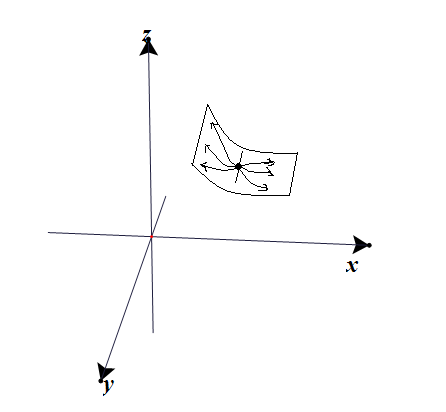
当然，这里只是简单地讲了(x,y)两个方向，动点(P)在曲面运动时可以取无数个方向（就像零向量有无数个方向），这些方向都与曲面相切(切平面)，当(P)任一方向((widehat{u}))的偏导数都为(0)时，(P)就是我们要求的点。
即

[frac{df}{ds}|_{widehat{u}}=0 ]

即

[ riangledown f cdot widehat{u}=0 ]

所以

[ riangledown f perp g ]

又因

[ riangledown g perp g ]

所以

[ecause riangledown f parallel riangledown g ]

证毕。

总结

目标函数为(f)，约束条件为(g=c),设(L=f+lambda g)，(lambda)为拉格朗日乘子，结合(g=c)求( riangledown L=0)的解，即为满足约束条件的极值.

注意：拉格朗日乘数法只能求极值，不能精确到极小值或极大值（像求导求极值一样），所以要代入试验。上述例子(f)并没有极大值，所以算出来的一定是极小值

可能讲得不太好，有兴趣猛戳下面：
拉格朗日乘数法MIT公开课