题解-[HNOI2001]遥控赛车比赛
前置知识:记忆化搜索、\(\texttt{Bfs}\)。
参考资料
跳转按钮
| 题解-[HNOI2001]遥控赛车比赛 |
|---|
| \(\texttt{Introduction}\) |
| \(\texttt{Description}\) |
| \(\texttt{Solution}\) |
| \(\texttt{Code}\) |
\(\texttt{Introduction}\)
蒟蒻练习历年省选题时遇见此题,\(\texttt{WA}\) 了好多发才 \(\texttt{AC}\),感到这题的巧妙足以记成题解。
\(\texttt{Description}\)
给你一个由 \(0\) 和 \(1\) 组成的 \(N\times M\) 地图,\(1\) 可走,\(0\) 是障碍。如果你反应力为 \(z\),那么你每次至少直走 \(z\) 步后才能转弯。起点为 \((sx,sy)\),终点为 \((tx,ty)\)。求反应力为 \(1\sim 10\) 时的最短路(如果到不了终点不输出,具体看题目链接)。
数据范围:\(1\le N,M\le 100\)。
\(\texttt{Solution}\)
这题是什么意思呢?如下图:
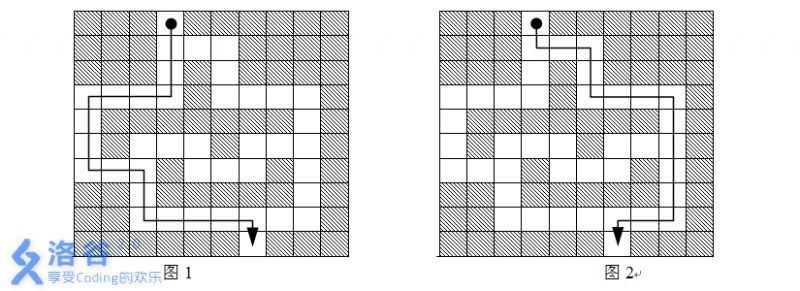
起点为 \((1,4)\),终点为 \((10,7)\)。
如果反应力为 \(1\),即走一步可以转个方向,那么最短路方案如图 \(2\),长度为 \(16\)。
如果反应力为 \(2\),即每直走两步可以换个方向,那么最短路方案如图 \(1\),长度为 \(18\)。
貌似很简单,做法很直接:\(\texttt{Bfs}\),记忆化搜索。
因为方向在这题中很重要,所以记录数组 \(dep_{i,j,k}\) 和 \(f_{i,j,k}\) 表示走到 \((i,j)\) 这个格子方向为 \(k\) 时在最短路条件下的路程和当前方向上直走了的距离(四个方向用 \(0,1,2,3\) 表示)。
然后每次 \(\texttt{Bfs}\) 拓展下一步路径的时候,特判一下,如果方向与 \(k\) 不同,那么必须满足 \(f_{i,j,k}\ge z\)。
看起来这题就只有普及的复杂度,但是如果你把代码敲出来一交,最多得个 \(50\) 分。
你会自闭很久直到找到反例——一个更令你自闭的东西:
路重复走,转 \(180^{\circ}\) 反而可能更优。
如下图:
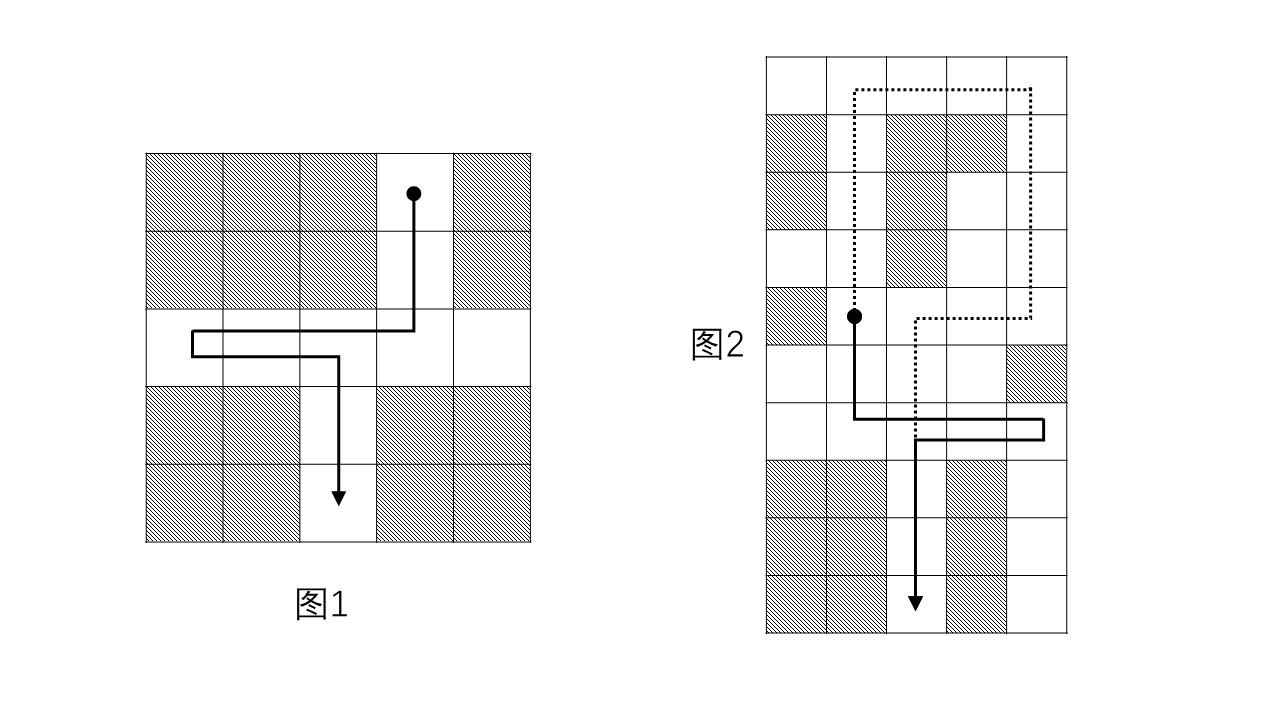
图 \(1\) 中的地图如果用你的代码只能跑反应力为 \(1\)。但是这种路径反应力为 \(2\) 可以跑!
同理,图 \(2\) 中如果走这种路重复走,转 \(180^{\circ}\) 的路径,长度可以减至 \(10\)(虚线路径为原计划路径,长度远大于 \(10\))。
那么题目貌似会变得很混乱:走过的地方也可以走,同一个位置更长的路径可能更优。
然而仔细思考后会发现,只有两种情况同一个位置的路径会更优:
-
更短。
-
当前方向上直走得更长。
其中第二种更优只能在继续直走中体现(如果转弯之前直走了多长没关系)。
然后敲个带个特判的记忆化广搜即可(普及知识不多说,特判会在代码中标识)。
\(\texttt{Code}\)
#include <bits/stdc++.h>
using namespace std;
//&Start
#define lng long long
#define lit long double
#define kk(i,n) "\n "[i<n]
const int inf=0x3f3f3f3f;
const lng Inf=1e17;
//&Debug
int open(0);
#define Debug if(open)
//&Data
const int N=110;
int n,m,maze[N][N],fx[4]={0,0,-1,1},fy[4]={-1,1,0,0};
struct Marco{int x,y,k;}s,t; //Bfs 状态
//&Bfs
const int Q=5e6+10;
int dep[N][N][4],f[N][N][4],ql,qr;
Marco q[Q];
int ok(int x,int y){return x>=1&&x<=n&&y>=1&&y<=m&&maze[x][y];}
int bfs(int z){
Debug printf("---%d---\n",z);//###
if(!ok(s.x,s.y)||!ok(t.x,t.y)) return -1;
memset(dep,0x3f,sizeof dep),memset(f,0,sizeof f);
int *D=dep[s.x][s.y],*F=f[s.x][s.y]; Marco tp;
D[0]=D[1]=D[2]=D[3]=F[0]=F[1]=F[2]=F[3]=0;//初始化起点
ql=1,qr=0,q[++qr]=(s.k=0,s),q[++qr]=(s.k=1,s),q[++qr]=(s.k=2,s),q[++qr]=(s.k=3,s);//起点可以是任意方向
while(qr>=ql){ //手模队列
tp=q[ql++];
Debug printf("%d %d %d\n",tp.x,tp.y,tp.k);//###
D=dep[tp.x][tp.y],F=f[tp.x][tp.y];
if(tp.x==t.x&&tp.y==t.y) return D[tp.k];//找到出口了!
for(int k=0;k<4;k++){
int xt=tp.x+fx[k],yt=tp.y+fy[k];
if(ok(xt,yt)&&(D[tp.k]+1<dep[xt][yt][k]||F[tp.k]>=f[xt][yt][k])){//特判:两种更优
if(k==tp.k){
dep[xt][yt][k]=D[tp.k]+1;//普通Bfs拓展
f[xt][yt][k]=F[tp.k]+1;
q[++qr]=(Marco){xt,yt,k};
} else if(F[tp.k]>=z&&D[tp.k]+1<dep[xt][yt][k]){//特判:要转弯即使直走得更长也没用
dep[xt][yt][k]=D[tp.k]+1;
f[xt][yt][k]=1;
q[++qr]=(Marco){xt,yt,k};
}
}
}
}
return -1;//被困住了,到不了出口
}
//&Main
int main(){
scanf("%d%d",&n,&m);
scanf("%d%d%d%d",&s.x,&s.y,&t.x,&t.y);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",maze[i]+j);
for(int i=1,tp;i<=10;i++)
if((tp=bfs(i))!=-1) printf("%d %d\n",i,tp);
else break;
return 0;
}
我还是太蒻了。祝大家学习愉快!