DS-博客作业06--图
1.本周学习总结(0--2分)
1.思维导图

2.谈谈你对图结构的认识及学习体会。
本章的图,因为和上一章的树上的比较紧凑,所以在考前一个星期也有看书背代码,也有理解代码和思路,但在考试的时候就是还不会!看着题目觉得挺简单的样子,打的代码还是错的!
在做课堂测试和课堂上互动来说,相比之前要会的多,之前一到填空题就感觉很难,现在一些填空也能下手了!
2.PTA实验作业(6分)
要求挑3道题目写设计思路、调试过程。设计思路用伪代码描述。题目选做要求:
题目必须是编程题,不要函数题!!!!!
2.1.题目1:7-1 图着色问题 (25 分)
图着色问题是一个著名的NP完全问题。给定无向图G=(V,E),问可否用K种颜色为V中的每一个顶点分配一种颜色,使得不会有两个相邻顶点具有同一种颜色?
但本题并不是要你解决这个着色问题,而是对给定的一种颜色分配,请你判断这是否是图着色问题的一个解。
输入格式:
输入在第一行给出3个整数V(0<V≤500)、E(≥0)和K(0<K≤V),分别是无向图的顶点数、边数、以及颜色数。顶点和颜色都从1到V编号。随后E行,每行给出一条边的两个端点的编号。在图的信息给出之后,给出了一个正整数N(≤20),是待检查的颜色分配方案的个数。随后N行,每行顺次给出V个顶点的颜色(第i个数字表示第i个顶点的颜色),数字间以空格分隔。题目保证给定的无向图是合法的(即不存在自回路和重边)。
输出格式:
对每种颜色分配方案,如果是图着色问题的一个解则输出Yes,否则输出No,每句占一行。
输入样例:
6 8 3
2 1
1 3
4 6
2 5
2 4
5 4
5 6
3 6
4
1 2 3 3 1 2
4 5 6 6 4 5
1 2 3 4 5 6
2 3 4 2 3 4
输出样例:
Yes
Yes
No
No
2.1.1设计思路(伪代码)
伪代码尽量文字描述,请用下面markdown符号渲染。如:
定义变量i表示XXXXX
for i=0 to n-1
a[i]执行运算等等。
end for
** 设计思路、伪代码要用```符号渲染 **
Judge()
{
if
{
比较颜色数是否符合要求,若不符合,返回 0;
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<vec[i].size();j++)
{
if()
判断顶点的颜色是否一样,若不一样,返回false;
}
}
}
2.1.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)
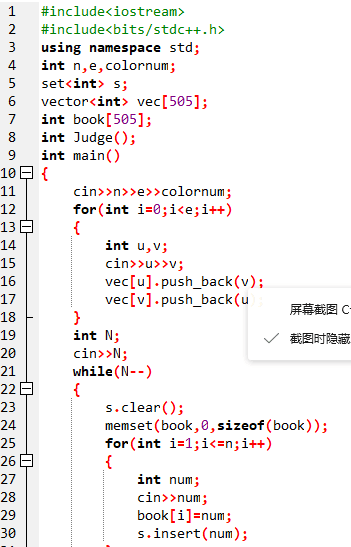

2.1.3本题PTA提交列表说明。
PTA提交列表中的每个错误详细说明为什么及如何解决。

- Q1:编译错误
- A1:在判断两顶点的颜色时,思路不太清晰,数组的变量写法有误。
2.2 题目2:7-3 六度空间 (30 分)
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。”如图1所示。
图1 六度空间示意图
“六度空间”理论虽然得到广泛的认同,并且正在得到越来越多的应用。但是数十年来,试图验证这个理论始终是许多社会学家努力追求的目标。然而由于历史的原因,这样的研究具有太大的局限性和困难。随着当代人的联络主要依赖于电话、短信、微信以及因特网上即时通信等工具,能够体现社交网络关系的一手数据已经逐渐使得“六度空间”理论的验证成为可能。
假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
输入格式:
输入第1行给出两个正整数,分别表示社交网络图的结点数N(1<N≤10
4
,表示人数)、边数M(≤33×N,表示社交关系数)。随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个结点的编号(节点从1到N编号)。
输出格式:
对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比,精确到小数点后2位。每个结节点输出一行,格式为“结点编号:(空格)百分比%”。
输入样例:
10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
输出样例:
1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%
2.2.1设计思路(伪代码)
main函数
for(j=1 to n)
for(i=1 to n)
初始化各点,visited为0
BFS返回值存于count
s= (count * 100.0) / n
end for
CreateAdj函数创建邻接表
for(i=1 to n)
初始化各节点第一条边为空
for(i=1 to e)
读入两节点a,b
b存入已申请内存的p->adjvex中
利用头插法将结点p插入a点首部
a插入b方法同上
end for
BFS函数
定义队列q,让结点v入队
将结点v标记为已访问
while(队列不空的时候)
temp=队首元素
队首元素出队并标记为已访问
while(p不为空)
if(p->adjvex未被访问)
该结点进队并标记为已访问
记录有联系结点个数的num加一
tail记录此时结点的值
end while
if(队首等于该层最后一个结点)
层数加一,last重置为队尾元素
if(层数为6)
此时可以不再进行结点记录,直接结束
最后返回记录标记的结点个数num
2.2.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)
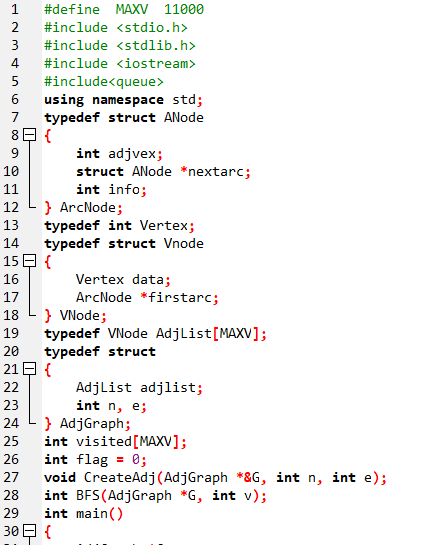



2.2.3本题PTA提交列表说明。
PTA提交列表中的每个错误详细说明为什么及如何解决。

- Q1:答案错误
- A1:代码出现了死循环,说明for中错了。
- Q2:编译错误
- A2:说明语法错误。
2.3 题目3:7-4 公路村村通 (30 分)
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
输入格式:
输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。
输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−1,表示需要建设更多公路。
输入样例:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例:
12
2.3.1设计思路(伪代码)
main()函数
{
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
{
用二维数组代表邻接矩阵,并进行初始化。
}
for (i = 1; i <= e; i++)
{
给邻接矩阵赋值
}
调用普里姆算法;
}
Prim() 函数
{
for (i = 1; i <= n; i++)
{
给lowcost[]和closest[]置初值;
}
for (i = 1; i <n; i++)
{
给min赋初值(表示无穷);
for (j = 1; j <= n; j++)
{
在(V-U)中找出离U最近的顶点k
k记录最近顶点的编号
}
for (j = 1; j <= n; j++)
{
对(V-U)中的顶点j 进行调整;
修改数组lowcost[]和closest[];
}
}
输出num;
}
2.3.2代码截图(注意,截图,截图,截图。不要粘贴博客上。)
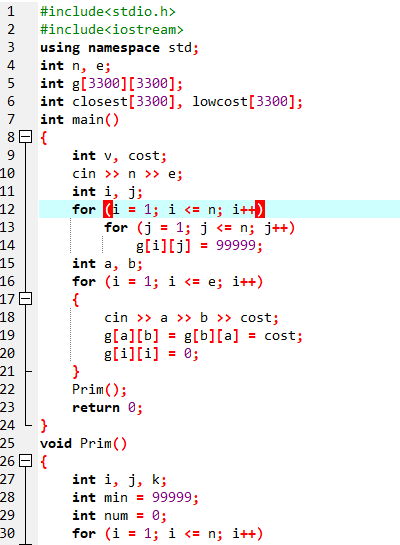


2.3.3本题PTA提交列表说明。
PTA提交列表中的每个错误详细说明为什么及如何解决。

- Q1:
- A1:
3、上机考试错题及处理办法(-2--2分)
3.1.1截图错题代码
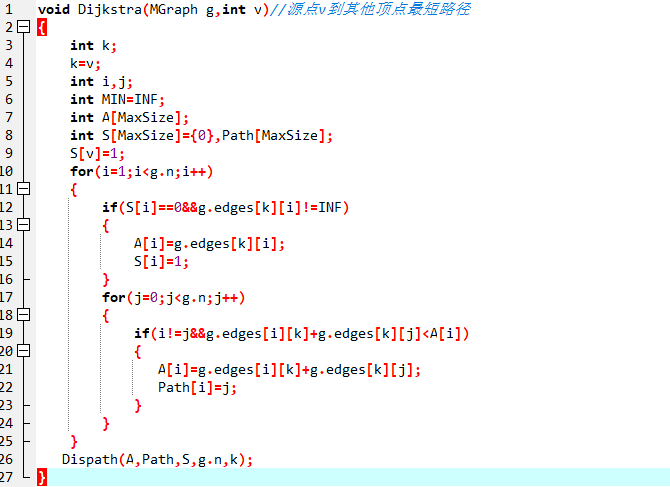
3.1.2 错的原因及处理方法
文字说明代码中那里错,怎么解决.
一直编译错误,运行框只,只输了一条边的两个顶点。错误的原因在于没有判断各顶点到其它顶点是否有边,及它的前驱顶点和该边的权重。递归口的参数也写得不对。处理方法:遍历图,进行距离初始化,S[]置空,和路径初始化。
3.2.1截图错题代码
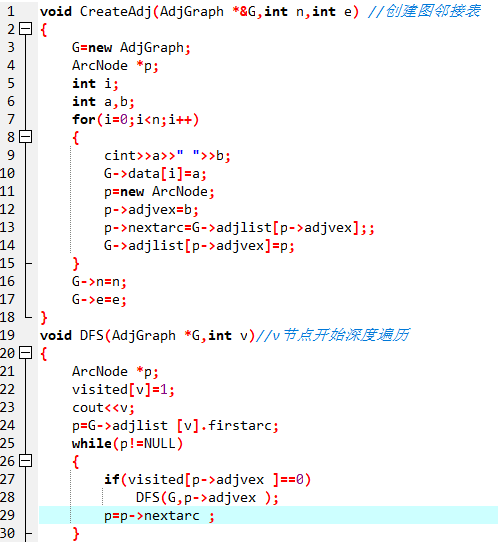
3.2.2 错的原因及处理方法
文字说明代码中那里错,怎么解决.
代码中在创建邻接表时,结构体的变量名使用得很混乱,导致建的图不完整。处理方法:看好结构体中的变量名,谨慎使用,搞懂它们的包含关系,然后用头插法建图。深度优先遍历好像没问题。但写得很慢,还是对算法不够熟悉,所以后面的深度优先遍历没时间写了。处理方法:借助队列来完成,采用层次遍历方式遍历图。定义环形队列指针并初始化队列。定义顶点访问标记数组且访问标记数组初始化,输出被访问顶点的编号和置为已访问标记。进队。队不空循环,出队一个顶点w.指向w的第一个邻接点,并查找w的所有邻接点。若当前邻接点未被访问,则访问该邻接点,然后置已访问标记,让该顶点进队,找下一个邻接点直至循环结束。