n的m划分
- 将n划分成若干个不超过m的数(正整数)的和,问有几种划分情况。
现在根据n和m的关系,考虑下面几种情况:
- 当n=1时,不论m的值为多少,只有一种划分,即{1};
- 当m=1时,不论n的值为多少,只有一种划分,即{1,1,1,....1,1,1}划分成n个1;
- 当n==m时,(a)划分中不包含n的情况,即n的n-1的划分f(n,n-1);(b)其他情况就是包含n的划分,只有1个,即{n};
- 当n>=m时,(a)划分中不包含m的情况,即n的n-1划分f(n,m-1);(b)其他情况就是包含m的划分,即{x1,x2,x3,x4,...,xi,m},也就是n-m的m划分f(n-m,m);
- 当n<m时,因为划分不会出现负数,因此也就是n的n划分。
综上的递推表达式为:
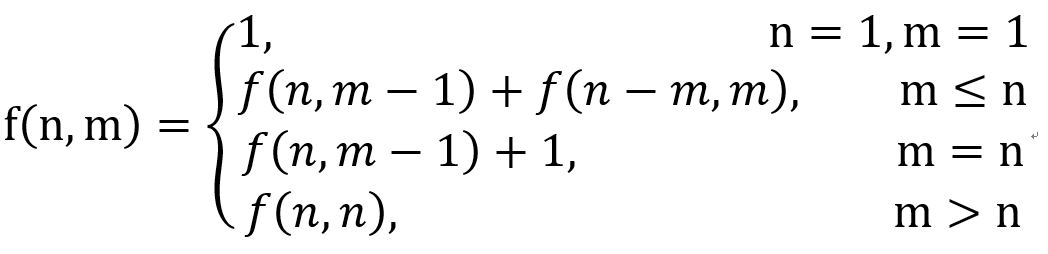
for(int i=1; i<=n; i++) { for(int j=1; j<=i; j++) { if(i==1||j==1) dp[i][j]=1; else { if(j==i) dp[i][j]=dp[i][j-1]+1; else if((i-j)<j) dp[i][j]=dp[i-j][i-j]+dp[i][j-1]; else dp[i][j]=dp[i-j][j]+dp[i][j-1]; } } }
- 将n划分成不超过m个数(正整数)的和,问有几种情况。
dp[i][j]表示j的i划分。
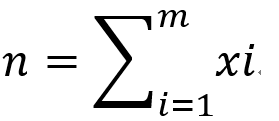
考虑n的m划分,如果对于每一个i都有xi>0,那么{xi-1}就对应了n-m的m划分。另外如果存在xi=0,那么就对应了n的m-1划分。
综上所述,对推关系:
dp[i][j]=dp[i][j-i]+dp[i-1][j]
dp[0][0]=1; for(int i=1;i<=m;i++) { for(int j=0;j<=n;j++) { if((j-i)>=0) dp[i][j]=(dp[i-1][j]+dp[i][j-i])%mod; else dp[i][j]=dp[i-1][j]; } }