这是第一场.先补一题,另外还有一个高精度的题目暂时不想研究.
G.Pot!!
首先被题面吓到了,看到一个整除的符号和一个数学式子以为是个数学题,于是没有注意到很明显的线段树的暗示.
细节:MUITIPLY的乘数x的范围是[2,10],这里面只有四个质数{2,3,5,7}.
由于序列中原本的所有数都是1,那么无论多少次操作之后,每个数都可以表示为1^a * 2^b * 3^c * 4^d * 5^e * ... * 10^j.
因此对于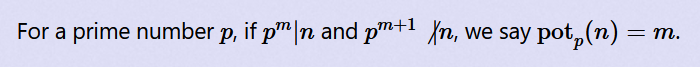
这里面的p只可能是{2,3,5,7},所以对于一个ai可以轻易求出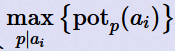 .
.
所以最后做法是用四个(分别存储四个质数作为因数的出现次数的)线段树维护区间信息.
照着书敲了个线段树板子,一遍就过了,问题就是板子记不住,也不算大碍吧= =
计算因数的时候用了multiset,自以为比较巧妙.

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> #include <string> #include <set> using namespace std; struct ST{ int l, r, big, sum; int tag; #define l(x) st[x][i].l #define r(x) st[x][i].r #define big(x) st[x][i].big #define tag(x) st[x][i].tag }st[400010][4]; // 2 3 5 7 int n, q; void spread(int p, int i){ if(!tag(p)) return; big(p * 2) += tag(p), big(p * 2 + 1) += tag(p); tag(p * 2) += tag(p), tag(p * 2 + 1) += tag(p); tag(p) = 0; } void change(int p, int l, int r, int x, int i){ if(l <= l(p) && r >= r(p)) { big(p) += x; tag(p) += x; return; } spread(p, i); int mid = l(p) + r(p) >> 1; if(l <= mid) change(p * 2, l, r, x, i); if(r > mid) change(p * 2 + 1, l, r, x, i); big(p) = max(big(p * 2), big(p * 2 + 1)); } void build(int p, int l, int r, int i){ l(p) = l, r(p) = r; if(l == r) {big(p) = 0; return;} int mid = l + r >> 1; build(p * 2, l, mid, i); build(p * 2 + 1, mid + 1, r, i); big(p) = max(big(p * 2), big(p * 2 + 1)); } int ask(int p, int l, int r, int i){ if(l <= l(p) && r >= r(p)) return big(p); spread(p, i); int mid = l(p) + r(p) >> 1; int ret = 0; if(l <= mid) ret = max(ret, ask(p * 2, l, r, i)); if(r > mid) ret = max(ret, ask(p * 2 + 1, l, r, i)); return ret; } int main(){ scanf("%d%d", &n, &q); for(int i = 0; i < 4; i++) build(1, 1, n, i); while(q--){ string opr; cin >> opr; if(opr[1] == 'U'){ // MULTIPLY int l, r, x; cin >> l >> r >> x; multiset<int> ms; while(!(x % 2)) ms.insert(2), x /= 2; while(!(x % 3)) ms.insert(3), x /= 3; while(!(x % 5)) ms.insert(5), x /= 5; while(!(x % 7)) ms.insert(7), x /= 7; for(const auto &i : ms) switch(i){ case 2: change(1, l, r, 1, 0); break; case 3: change(1, l, r, 1, 1); break; case 5: change(1, l, r, 1, 2); break; case 7: change(1, l, r, 1, 3); break; } }else{ // MAX int l, r; cin >> l >> r; int ans = 0; for(int i = 0; i < 4; i++) ans = max(ans, ask(1, l, r, i)); cout << "ANSWER " << ans << endl; } } return 0; }
H - Delivery Route
不是正解,用SPFA优化卡过去了.
给出一张含有负权边的图,求单源最短路,1<=n<=25000,2<=m<=150000.
有负边,SPFA复杂度又不够,于是SLF优化.
STL依赖症被治好了,手写双端队列,链式向前星.
关于这个SLF的原理,我还在找博文,再看看.

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> #include <cmath> using namespace std; #define INF 0x3F3F3F3F struct E { int to = 0, wei = 0, nxt = 0; } e[150010]; int head[25010], ind = 1; int n, x, y, s, dist[25010]; int q[20000010], l = 1e7, r = 1e7, val = 0; bool used[25010]; inline void add(int x, int y, int w) { e[ind].to = y; e[ind].wei = w; e[ind].nxt = head[x]; head[x] = ind++; } inline int read() { char ch = getchar(); int x = 0, f = 1; while (ch > '9' || ch < '0') { if (ch == '-') f = -1; ch = getchar(); } while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); } return x * f; } int main() { n = read(), x = read(), y = read(), s = read(); while (x--) { int a = read(), b = read(), c = read(); add(a, b, c); add(b, a, c); val += 2 * c; } while (y--) { int a = read(), b = read(), c = read(); add(a, b, c); val += c; } val = sqrt(val) / 100; memset(dist, 0x3F, sizeof(dist)); q[l] = s; dist[s] = 0; used[s] = true; while (l <= r) { int cur = q[l]; l++; used[cur] = false; for (int i = head[cur]; i; i = e[i].nxt) if (dist[e[i].to] > dist[cur] + e[i].wei) { dist[e[i].to] = dist[cur] + e[i].wei; if (!used[e[i].to]) { used[e[i].to] = true; if (l <= r && dist[e[i].to] < dist[q[l]] + val) q[--l] = e[i].to; else q[++r] = e[i].to; } } } for (int i = 1; i <= n; i++) if (dist[i] != INF) printf("%d ", dist[i]); else puts("NO PATH"); return 0; }
