本文引用部分转载自此博文.
1.超级源点
我在一篇反向建图相关的文章里写到利用反向建图求解多个起点到一个终点的最短路问题,这个问题也可以使用一个叫做超级源点的方法在同样复杂度下求解.
背景:给出题目,在一张图中有多个点起点,一个终点,求所有起点到终点的最短距离。
解题方法:
1.跑N边单源最短路,但是这样是不行的肯定超时。
2.floyd求出所有最短路,枚举每个起点到终点的距离,这个似乎比法1更慢。
3.反向建边,反向跑一遍Dijkstra,或者SPFA,这样就能求到终点到起点的距离,在枚举最小的一个即可,时间复杂度为一遍最短路加枚举N。
4.建立超级源点,虚拟出一个点作为源点,源点到所有起点的距离都是0,那么这样求超级源点到终点的最短距离就是所有起点到终点的距离的最短一个,时间复杂度为一遍最短路。
所以"超级源点"意思就是把所有的起点联系在了一起,使得最短路算法处理时更加简便.
实际上并不一定需要虚拟节点到所有起点的距离都是0,根据实际情况可以虚拟一个用来表示起始状态的节点.
(之所以虚拟一个起始状态节点,是因为有时候给出的节点中不含有可以表示起始状态的)
这里使用最短路算法,最短路的含义即为最小金币花费数.
通过题目的含义可以把每一种物品都看作一个节点,并在这些节点之间建立带权有向边,另外再处理一下"地位"的限制条件就可以跑SPFA.
但是在这些物品当中,怎么选择起点呢?任意一个物品都可以作为起点,花费一定的金币直接买下.
暴力枚举起点跑SPFA可以通过,更好的方法是建立虚拟节点表示什么也没买,花费了0金币的状态,这个状态的下一步可以是直接购买了任意一个物品并花费了相应的金币.以这个节点作为唯一起点跑一遍SPFA即可.
2.超级汇点
题目二:给出一张图中有一个起点,有多个终点,求一个起点到所有终点的最短距离。
解题方法:
1.直接忽略floyd
2.一遍最短路(SPFA或Dijkstra),枚举N。
3.建立超级汇点,所有终点到汇点的距离为0,一遍最短路即可的出答案。
与超级源点类似理解即可.
一道综合题:
The Shortest Path in Nya Graph
大意:给出一张有N个节点,M条加权边的无向图,其中的每一个节点都属于某一层x(1<=x<=N),第x层的任意一个节点总是可以(不需要通过边)花费C来到达第x+1,x-1层的任意一个节点.
在这张图中计算节点1到达节点N的最短路.数据范围达到1e5.
所有企图存边或者遍历边的想法都以MLE或TLE告终了.
现在发现如下特性:
1.由于最短路算法的性质,只需要考虑相邻层级之间的边,跨层级总是可以通过若干个相邻层级的边来完成.
2.对于某层级中的点,其花费C可以到达相邻层级中的任意点.
性质2可以通过对每层先设置一个虚拟节点,该虚拟节点以自己为起点向其层级中的所有节点都连接一条权值为0的有向边,再设置另一个虚拟节点,其层级中所有节点以自己为起点向该虚拟节点连接一条权值为0的边.
假设有三层,每层用同一个大写字母表示:(暂时忽略一下原有的边)
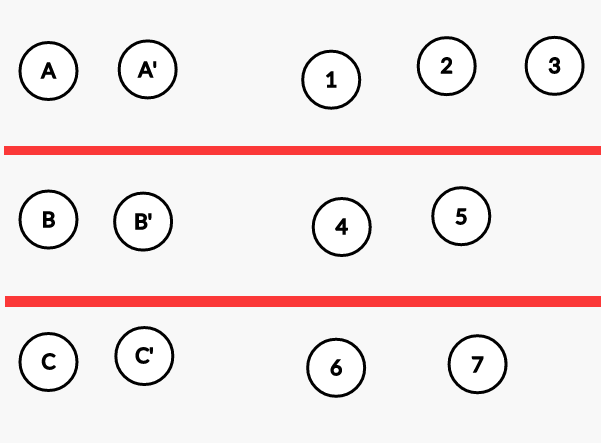
现在根据上面的表述连接虚拟节点,没有标边权的边视为0:
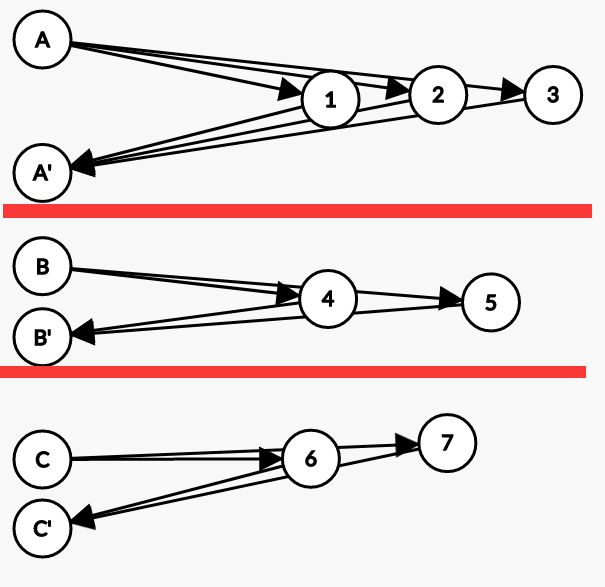
如此,现在想要让某个节点想要到达相邻层,总是有一条唯一路径,对虚拟节点进行如下连接:
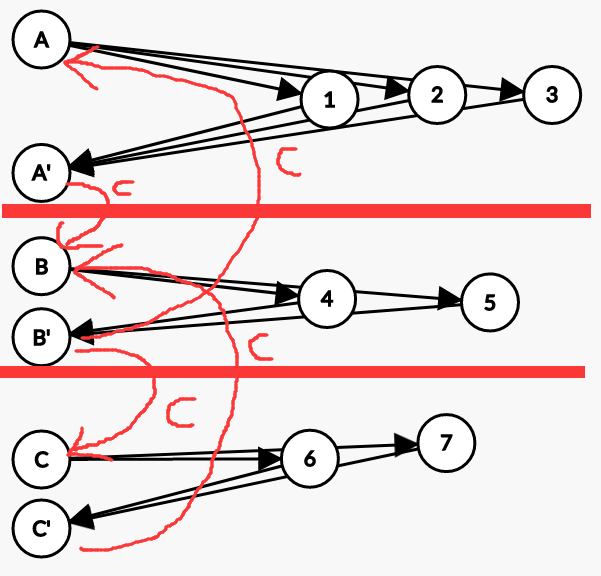
(图丑,不过想必也没有多少人来看我的博客╮(╯-╰)╭)
好了,现在在这张图上跑Dijkstra就可以了.
沉迷vecotr让我的实现看起非常密集.
#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> #include <queue> using namespace std; struct E { int to, wei; bool operator<(const E& other) const { return wei > other.wei; } }; priority_queue<E> q; vector<E> e[400010]; vector<int> l[100010]; int n, m, c, lv[400010], dist[400010]; bool usedl[100010]; inline int read() { char ch = getchar(); int x = 0, f = 1; while (ch > '9' || ch < '0') { if (ch == '-') f = -1; ch = getchar(); } while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); } return x * f; } void solve() { memset(dist, -1, sizeof(dist)); memset(usedl, 0, sizeof(usedl)); n = read(), m = read(), c = read(); for(int i = 1; i <= n; i++) l[i].clear(), l[i + n].clear(), l[i + 2 * n].clear(); for (int i = 1; i <= n; i++) { lv[i] = read(), l[lv[i]].push_back(i); usedl[lv[i]] = true; e[i].clear(), e[i + n].clear(), e[i + 2 * n].clear(); } while (m--) { int u = read(), v = read(), w = read(); e[u].push_back({v, w}); e[v].push_back({u, w}); } for(int i = 1; i < n; i++){ if(usedl[i] && usedl[i + 1]){ lv[i + n] = lv[i + 2 * n] = i; // A, A' lv[i + 1 + n] = lv[i + 1 + 2 * n] = i + 1; // B, B' for(vector<int>::iterator j = l[i].begin(); j != l[i].end(); j++) e[i + n].push_back({*j, 0}), e[*j].push_back({i + 2 * n, 0}); for(vector<int>::iterator j = l[i + 1].begin(); j != l[i + 1].end(); j++) e[i + 1 + n].push_back({*j, 0}), e[*j].push_back({i + 1 + 2 *n, 0}); e[i + 2 * n].push_back({i + 1 + n, c}); e[i + 1 + 2 * n].push_back({i + n, c}); } } q.push({1, 0}); while (!q.empty()) { E cur = q.top(); // printf("!!!%d %d ", cur.to, cur.wei); q.pop(); if (dist[cur.to] != -1) continue; dist[cur.to] = cur.wei; for(vector<E>::iterator i = e[cur.to].begin(); i != e[cur.to].end(); i++) if(dist[i->to] == -1) q.push({i->to, cur.wei + i->wei}); } printf("%d ", dist[n]); } int main() { // freopen("in.txt", "r", stdin); int t = read(); for (int i = 1; i <= t; i++) { printf("Case #%d: ", i); solve(); } return 0; }