[模板]最近公共祖先LCA(树上倍增)

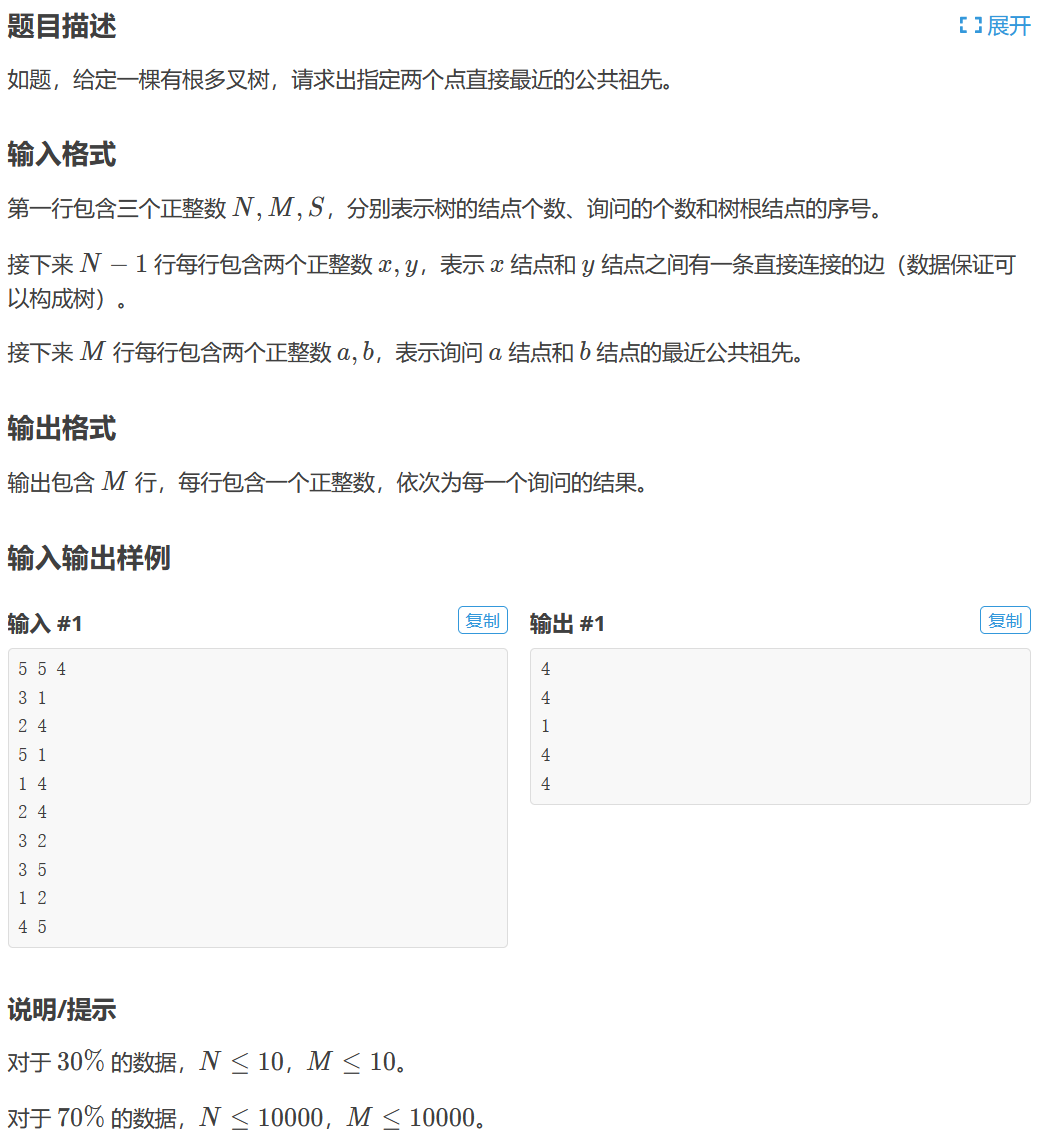
对于LCA问题,很容易想到如下做法:

　　1. 选取一个节点不停向上走直到根节点,标记经过的所有节点.

　　2. 再从另一个节点不停向上走,遇到的第一个标记的节点即为LCA.

显然会TLE,这里介绍树上倍增方法.

---

假设需要求解LCA(x, y),采用与暴力同样的思想,现在需要进行一种处理使得其效率大幅提高.

预先处理得到节点i的深度为dep[i],观察到,设dep[x]<=dep[y],那么dep[LCA(x, y)]<=dep[x].

让y先"爬树"(dep[y]减小)到dep[x],那么之后x与y再一起"爬树".

需要寻找一种足够快的方法让y爬到dep[x].

运用倍增方法进行一些预处理可以达到这个目的:

设f[x][k]表示x的2^k辈祖先,如f[x][0]即x的父节点,且对∀k∈[1,log n],f[x][k]=f[f[x][k-1]][k-1].

花费O(N log N)时间进行此预处理:

    for (int i = 1; (1 << i) <= n; i++)
        for (int j = 1; j <= n; j++) f[j][i] = f[f[j][i - 1]][i - 1];

现在想要让y快速爬树,观察下面这个运用了二进制拆分思想的代码:

    int t = log(n) / log(2) + 1;

    for(int i = t; i >= 0; i--)
        if(dep[f[y][i]] >= dep[x]) y = f[y][i]; 　　// 注意这会使得dep[y]减小而不是增大

这样进行"爬树"花费O(log N)时间,且最后一定有dep[x]==dep[y].

之后令x,y一起爬树,注意到这是一个有单调性的问题,即若LCA(x,y)==z, 那么z的所有祖先都是x,y的公共祖先,所以有如下的倍增方法:

仍然是二进制拆分.

    if(x == y) return x;
    for(int i = t; i >= 0; i--)
        if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];

花费时间相同.

同样使用倍增求解的问题还有RMQ.

#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;

vector<int> e[500010];
int n, m, s;
int dep[500010], f[1000010][30];

void dfs(int x, int d) {
    dep[x] = d;
    for (auto i : e[x])
        if (!dep[i]) dfs(i, d + 1), f[i][0] = x;
}
int LCA(int x, int y) {
    int t = log(n) / log(2) + 1;
    if (dep[x] > dep[y]) swap(x, y);

    for(int i = t; i >= 0; i--)
        if(dep[f[y][i]] >= dep[x]) y = f[y][i];

    if(x == y) return x;
    for(int i = t; i >= 0; i--)
        if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];

    return f[x][0];
}

int main() {
    scanf("%d%d%d", &n, &m, &s);
    for (int i = 1; i < n; i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        e[x].push_back(y);
        e[y].push_back(x);
    }
    f[s][0] = s;
    dfs(s, 1);
    for (int i = 1; (1 << i) <= n; i++)
        for (int j = 1; j <= n; j++) f[j][i] = f[f[j][i - 1]][i - 1];

    for (int i = 1; i <= m; i++) {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d
", LCA(l, r));
    }

    return 0;
}