维护一个栈,使得其存储的数据具有单调性,这样的栈叫做单调栈.
- 单调递增栈:数据从栈顶到栈底单调递增.
- 单调递减栈:数据从栈顶到栈底单调递减.
单调栈何时用:为任意一个元素找左边和右边第一个比自己大/小的位置用单调栈.
用递增单调栈还是递减单调栈:递减栈会剔除波谷留下波峰;递增栈剔除波峰留下波谷.
由于每个元素最多各自进出栈一次,复杂度是O(n).
对所有元素,找到其右边第一个大于该元素的位置,此题用单调递增栈.本题要求出下标,而单调栈可以很容易地找出元素,可以使用pair把元素和下标绑定起来处理.接下来只需要利用单调栈算法找到一个元素右侧第一个大于该元素的元素即可.
此题可以视为没有重复元素处理.
用矩形高度对应数字大小,以这个数据为例:
5 4 2 1 3 5
设置一个栈,从左到右依次处理这个数列:
4入栈:

现在栈里只有4,找不到右侧比4大的元素.
2和1入栈:
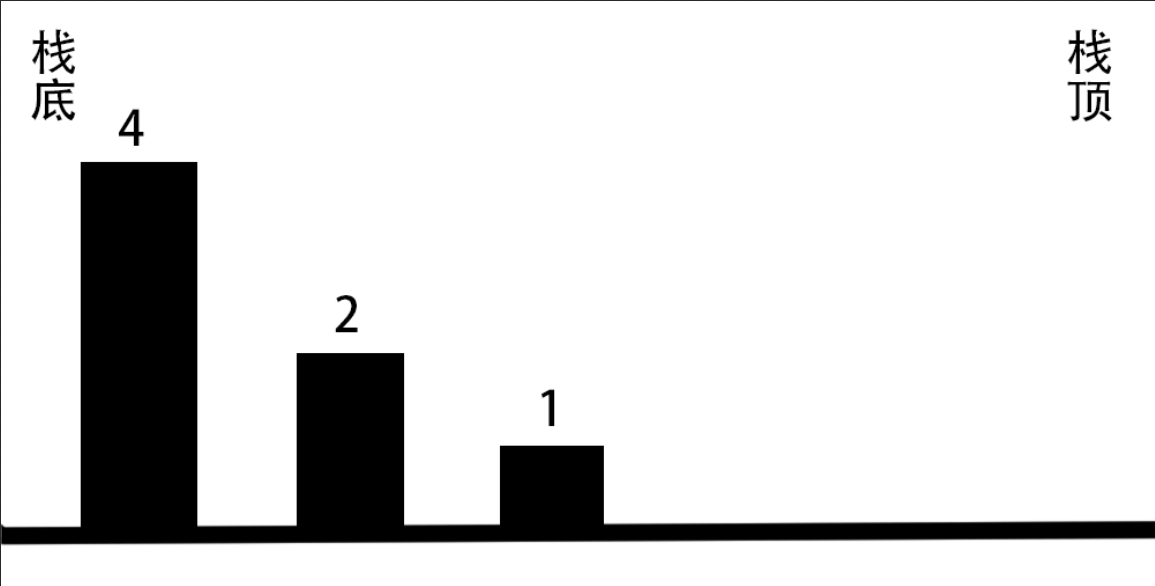
对于任意元素都没有在其右侧找到比他更大的元素.此时从栈顶到栈底是单调递增的,这是一个单调递增栈.
只要新的元素比栈顶小,就直接把新元素入栈.凡是处在栈内的元素都还没有找到它的解.
下一个元素是3,如果直接入栈会破坏栈的单调性:
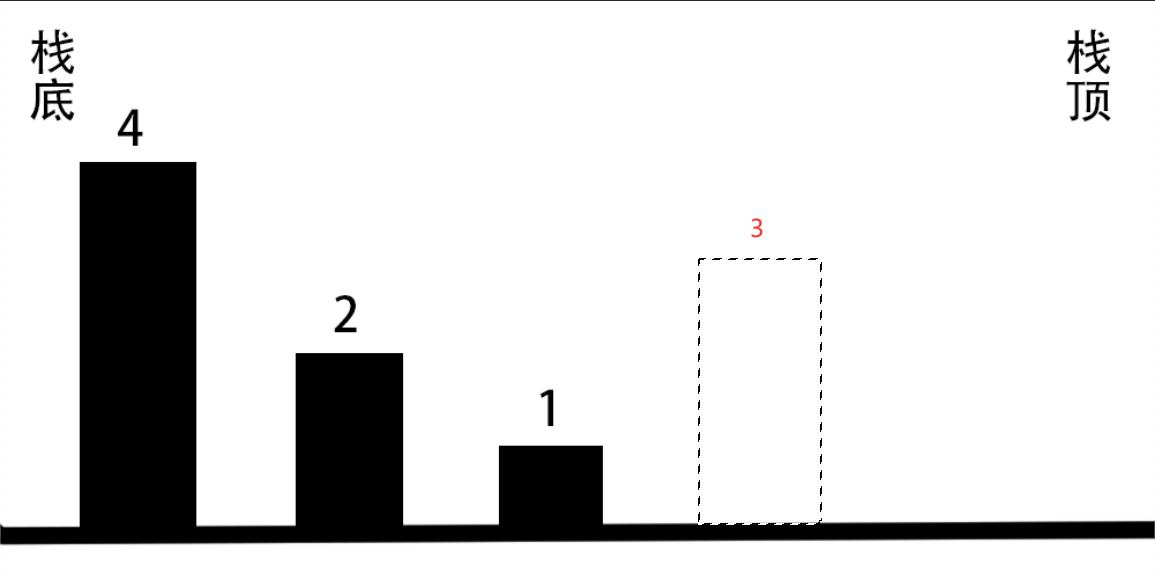
假设3直接入栈了,会发现2和1都发现了其右侧第一个大于他们的元素,即3.
此时2和1找到了解,这就意味着不需要考虑3之后的元素会不会是他们的解了,并且2和1也不会成为之后元素的解,那么2和1就完全没有必要留在栈中了.
所以在3入栈之前把1,2弹出并记录其解为3,然后使3入栈.4对于单调性不受到也不产生影响.

这使得栈保持了从栈顶到栈底递增的状态.
现在尝试让5入栈,发现将会破坏单调性,于是从栈顶不断弹出元素直到使5入栈时单调性不改变.
依次弹出3,4并记录他们的解为5.然后5入栈.

已经没有剩余的元素需要处理了,现在要处理栈中剩下的元素.
由于任意时刻栈中元素一定是从栈顶到栈底单调递增的,所以此时栈中所有元素右侧元素都比自己小,从而得知他们都没有解.(现在让他们直接出栈即可,也可以放置不管)
至此,所有元素都处理完毕,即找到了解或者发现没有解.
这个过程中遵循了如下原则进行操作:
①对原数列从左到右依次处理.
②对于处理的每一个数,如果当前栈为空或者该数小于栈顶的数,使该数入栈.
③对于处理的每一个数,如果该数大于栈顶的数,不断地弹出栈顶直到该数小于栈顶的数或者栈为空.然后该数入栈.
④在③过程中,每弹出一个栈顶的数,就记录该数的解为正在处理的数.
上述原则可以在代码里体现,其中②③进行了融合.

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> #include <stack> using namespace std; typedef pair<int, int> P; stack<P> s; int n, ans[3000010], a[3000010]; int main(){ scanf("%d", &n); for(int i = 1; i <= n; i++){ scanf("%d", a + i); while(!s.empty() && s.top().first < a[i]){ ans[s.top().second] = i; s.pop(); } s.push(make_pair(a[i], i)); } for(int i = 1; i <= n; i++) printf("%d ", ans[i]); return 0; }
有如下性质:
①任意时刻,从栈顶到栈底的数总是单调递增的.
②所有元素在未入栈或者未入栈时是尚未找到解的.
③所有元素出栈时一定已经找到了解.
④所有元素一定各自入栈和出栈一次.
⑤当且仅当将要入栈的元素会破坏栈的单调性(或者没有可入栈的元素)时才会有元素出栈.
由③和⑤得知:
⑥每当新元素会破坏栈的单调性时就会有元素找到了解.
⑦已经找到解的元素(从栈顶)出栈不会影响后续的求解.
这里的"解"对应本题指的时一个元素右侧第一个大于该元素的元素.
根据性质⑥,如果发现问题抽象化之后发现解总是伴随着单调性的变化而产生,就要考虑单调栈算法.
以P1901 发射站为例,对于一个发射站,需要找到左右两侧最近的且比他高的发射站.想象有一排从左到右单调递减(因此很容易找到左侧解)的发射站,如果右侧加入一个比较高的新发射站使得单调性破坏,那么新发射站左边一定有发射站找到了右侧解,这些发射站的解就都找到了.(题意已经说明不存在重复元素)

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> #include <stack> using namespace std; typedef struct { int h, v, idx; } S; stack<S> s; int n, ans[1000010], big; int main() { scanf("%d", &n); for (int i = 1; i <= n; i++) { int a, b; scanf("%d%d", &a, &b); while (!s.empty() && s.top().h < a) { S tmp = s.top(); s.pop(); ans[i] += tmp.v; if (!s.empty()) ans[s.top().idx] += tmp.v; } s.push({a, b, i}); } while (!s.empty()) { S tmp = s.top(); s.pop(); if (!s.empty()) ans[s.top().idx] += tmp.v; } for (int i = 1; i <= n; i++) big = max(big, ans[i]); printf("%d ", big); return 0; }
对于有重复元素的问题,如果可能的话可以把重复次数视为权值考虑进行求解.

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> #include <stack> using namespace std; typedef pair<int, int> P; int n; long long ans; stack<P> s; int main() { scanf("%d", &n); while (n--) { int h; scanf("%d", &h); P p(h, 1); while (!s.empty() && s.top().first <= h) { ans += s.top().second; if (s.top().first == h) p.second += s.top().second; s.pop(); } if (!s.empty()) ans++; s.push(p); } printf("%lld ", ans); return 0; }
更复杂一点的处理,见直方图中最大的矩形题解区.

