一.基础并查集(模板)
int fa[SIZE]; int get(int x) { if (fa[x] == x) return x; return fa[x] = get(fa[x]); } void merge(int x, int y) { fa[get(x)] = fa[get(y)]; } for(int i = 1; i <= SIZE; i++) fa[i] = i;
你也可以这样写:
int get(int x) { return fa[x] == x ? x : fa[x] = get(fa[x]); } void merge(int x, int y) { fa[get(y)] = fa[get(x)]; }
一般使用路径压缩就足以保证平均复杂度了.此时单次操作的复杂度可视为O(log n).
并查集的每个集合内部的元素具有某种共同特征,在下面这题中,同一个集合内部的所有村庄都是互相联通的,而不属于同一个集合的两个村庄一定不联通.
近乎于并查集的模板题,把将要修复的公路按照时间升序排列,每修复一条公路即合并公路两端的村庄到一个集合内,集合内的任意村庄之间是相通的.
每次合并村庄检查是否已经联通全部村庄,联通时即为最短用时.

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> using namespace std; struct S { int x, y, t; } s[100010]; int n, m, fa[1010]; bool cmp(S a, S b) { return a.t < b.t; } int get(int x) { if (fa[x] == x) return x; return fa[x] = get(fa[x]); } void merge(int x, int y) { fa[get(x)] = fa[get(y)]; } bool check(){ int rt = get(1); for(int i = 2; i <= n; i++) if(get(i) != rt) return false; return true; } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= m; i++) scanf("%d%d%d", &s[i].x, &s[i].y, &s[i].t); for (int i = 1; i <= n; i++) fa[i] = i; sort(s + 1, s + 1 + m, cmp); if(check()){puts("0"); return 0;} for(int i = 1; i <= m; i++){ merge(s[i].x, s[i].y); if(check()){printf("%d ", s[i].t); break;} } if(!check()) puts("-1"); return 0; }
相似的题目有P3958 [NOIP2017 提高组] 奶酪,类似于上一题,同一个集合内部的空洞一定是联通的,不属于同一个集合的两个空洞一定不连通.数据范围很小.

#include <algorithm> #include <cmath> #include <cstdio> #include <cstring> #include <iostream> using namespace std; struct S { long long x, y, z; } s[1010]; int n, fa[1010]; long long h, r; int get(int x) { if (fa[x] == x) return x; return fa[x] = get(fa[x]); } void merge(int x, int y) { fa[get(x)] = fa[get(y)]; } bool iscon(S a, S b) { return (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y) + (a.z - b.z) * (a.z - b.z) <= 4 * r * r; } void solve() { scanf("%d%lld%lld", &n, &h, &r); for (int i = 1; i <= n; i++) fa[i] = i; for (int i = 1; i <= n; i++) { scanf("%lld%lld%lld", &s[i].x, &s[i].y, &s[i].z); for (int j = 1; j <= i - 1; j++) if (iscon(s[i], s[j])) merge(i, j); } if (n == 1) { if (s[1].z - r <= 0 && s[1].z + r >= h) puts("Yes"); else puts("No"); return; } else for (int i = 1; i <= n - 1; i++) for (int j = i + 1; j <= n; j++) { if (get(i) == get(j) && (s[i].z - r <= 0 && s[j].z + r >= h || s[j].z - r <= 0 && s[i].z + r >= h)) { puts("Yes"); return; } } puts("No"); } int main() { // freopen("in.txt", "r", stdin); // freopen("out.txt", "w", stdout); int t; scanf("%d", &t); while (t--) solve(); return 0; }
再复杂一点的有P1525 [NOIP2010 提高组] 关押罪犯,可以用边带权的并查集,这里用的是标记和普通并查集的方法.在同一座监狱的罪犯在一个集合里.

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> using namespace std; struct S { int x, y, c; } s[100010]; int n, m, fa[20010], enm[20010]; bool cmp(S fa, S enm) { return fa.c > enm.c; } int get(int x) { if (fa[x] == x) return x; return fa[x] = get(fa[x]); } void merge(int x, int y) { fa[get(x)] = fa[get(y)]; } bool check(int x, int y) { return get(x) == get(y); } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i++) fa[i] = i; for (int i = 1; i <= m; i++) scanf("%d%d%d", &s[i].x, &s[i].y, &s[i].c); sort(s + 1, s + m + 1, cmp); for (int i = 1; i <= m; i++) { if (check(s[i].x, s[i].y)) { printf("%d", s[i].c); return 0; } else { if (!enm[s[i].x]) enm[s[i].x] = s[i].y; else merge(enm[s[i].x], s[i].y); if (!enm[s[i].y]) enm[s[i].y] = s[i].x; else merge(enm[s[i].y], s[i].x); } } puts("0"); return 0; }
P1955 [NOI2015] 程序自动分析,离散化后使用并查集处理.题意比较直白.

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> using namespace std; #define SIZE 1000000 int n, fa[SIZE + 10], dis[2 * SIZE + 10], idx; struct S { int x, y, e; } s[SIZE]; int get(int x) { if (x == fa[x]) return x; return fa[x] = get(fa[x]); } void merge(int x, int y) { fa[get(x)] = get(y); } void init() { for (int i = 0; i <= n * 2 + 1; i++) fa[i] = i; } void discrete() { sort(dis + 1, dis + 1 + idx); idx = unique(dis + 1, dis + 1 + idx) - dis - 1; } int query(int x) { return lower_bound(dis + 1, dis + 1 + idx, x) - dis; } bool cmp(S &a, S &b) { return a.e > b.e; } void solve() { scanf("%d", &n); init(); idx = 0; for (int i = 1; i <= n; i++) { scanf("%d%d%d", &s[i].x, &s[i].y, &s[i].e); dis[++idx] = s[i].x; dis[++idx] = s[i].y; } discrete(); sort(s + 1, s + 1 + n, cmp); for (int i = 1; i <= n; i++){ int nx = query(s[i].x), ny = query(s[i].y); if (s[i].e) merge(nx, ny); else if (get(nx) == get(ny)) { puts("NO"); return; } } puts("YES"); } int main() { // freopen("out.txt", "w", stdout); int t; scanf("%d", &t); while (t--) solve(); return 0; }
二.拓展域并查集
在P2024 [NOI2001] 食物链中,题目明确指出有三类动物A,B,C,并且有循环的捕食关系
设置三倍大小的并查集:
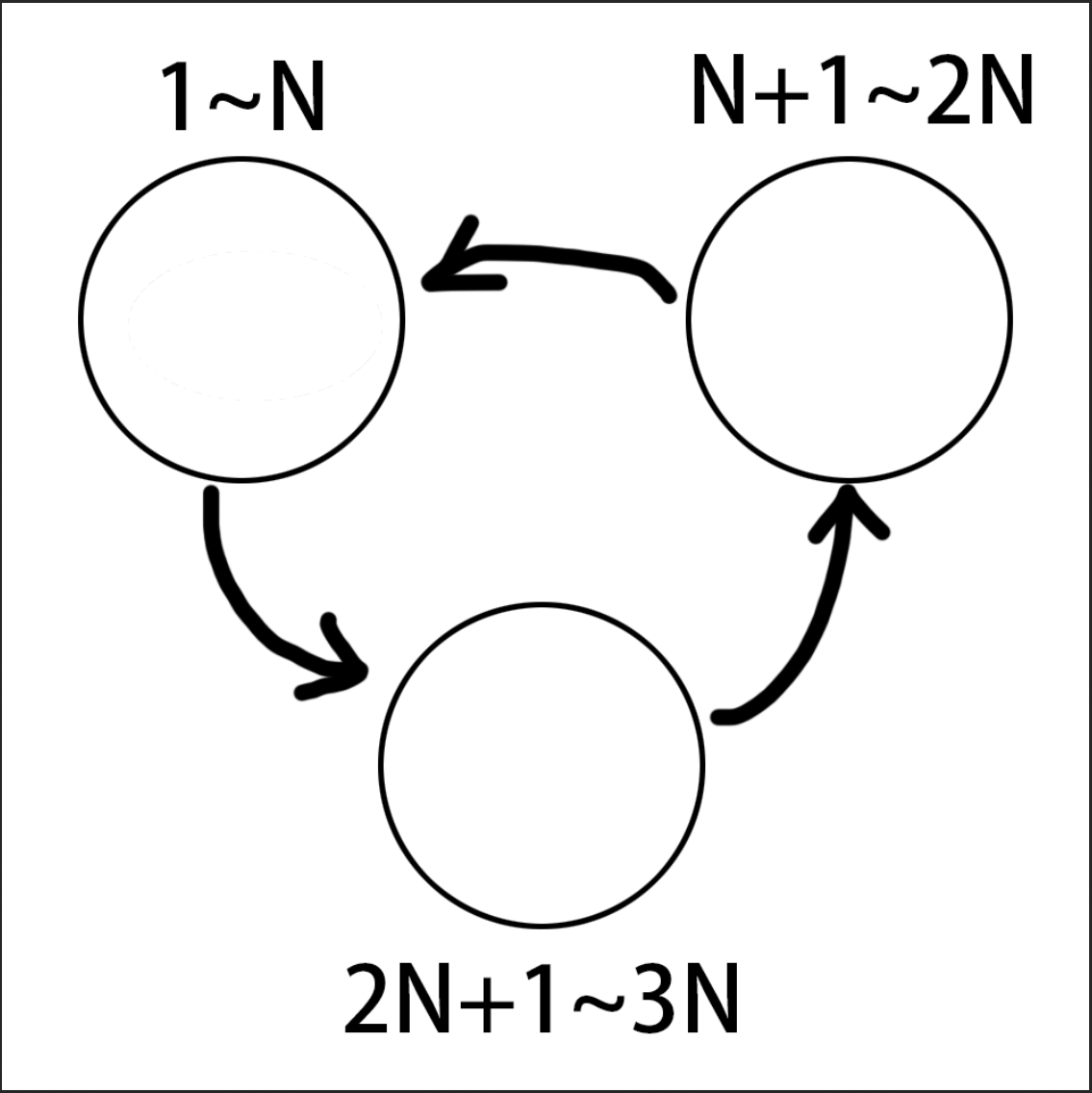
这三个圆圈称为"域".
那么现在,对于任一动物x(x∈[1,N]),其都有唯一确定的三个域 :同类域(x),猎物域(x+N),天敌域(x+2N).(也就是三个集合)
若动物y是x的同类,那么其三个域相同,对应合并他们的三个域.
若动物y是x的猎物,那么x的同类域(x)是y的天敌域(y+2N),x的猎物域(x+N)是y的同类域(y),x的天敌域(x+2N)是y的猎物域(y+N).对应合并这些域.
每次合并之前判断一下当前条件是否满足,例如当给出关系x与y是同类时,检查y是否在x的天敌域或者捕食域.
拓展域作为一种并查集的使用思想,相对于边带权的并查集不需要对基础并查集的实现进行任何修改.

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> using namespace std; int n, k, ans, fa[200000]; int get(int x) { if (x == fa[x]) return x; return fa[x] = get(fa[x]); } void merge(int x, int y) { fa[get(x)] = get(y); } int main() { scanf("%d%d", &n, &k); for (int i = 1; i <= 3 * n; i++) fa[i] = i; while (k--) { int opr, x, y; scanf("%d%d%d", &opr, &x, &y); if (x > n || y > n) { ans++; continue; } if (opr == 1) { if (get(x) == get(y + n) || get(x) == get(y + n + n)) ans++; else { merge(x, y); merge(x + n, y + n); merge(x + n + n, y + n + n); } } else { if (x == y || get(x) == get(y) || get(x) == get(y + n)) ans++; else { merge(x, y + 2 * n); merge(x + n, y); merge(x + 2 * n, y + n); } } } printf("%d ", ans); return 0; }
(本文以下所有内容都属于边带权的并查集)
三.维护集合大小的并查集
只需要将基础并查集的merge修改为:
int siz[SIZE]; // siz全部元素要初始化为1 void merge(int x, int y) { x = get(x), y = get(y); if (x != y) { fa[x] = y; siz[y] += siz[x]; } }
之后,元素v所在集合的大小(元素个数)表示为siz[get(v)].此时边的权即为集合的大小.
P4185 [USACO18JAN]MooTube G 此题中在排序后处理每个合并操作时顺便也更新了集合大小,最后输出给定元素所在集合的大小减去一(该元素自身)即可.如果每次合并后都枚举所有元素计算则会提高复杂度(从而TLE).

#include <algorithm> #include <cstdio> #include <cstring> #include <iostream> using namespace std; struct S { int x, y, r; } s[100010]; struct Q { int k, v, num; } q[100010]; int n, m, fa[100010], siz[100010], ans[100010]; bool cmp1(Q a, Q b) { return a.k > b.k; } bool cmp2(S a, S b) { return a.r > b.r; } int get(int x) { if (fa[x] == x) return x; return fa[x] = get(fa[x]); } void merge(int x, int y) { x = get(x), y = get(y); if (x != y) { fa[x] = y; siz[y] += siz[x]; } } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n - 1; i++) scanf("%d%d%d", &s[i].x, &s[i].y, &s[i].r), fa[i] = i, siz[i] = 1; fa[n] = n, siz[n] = 1; for (int i = 1; i <= m; i++) { scanf("%d%d", &q[i].k, &q[i].v); q[i].num = i; } sort(q + 1, q + 1 + m, cmp1); sort(s + 1, s + 1 + n, cmp2); int p1 = 1, p2 = 1; // p1 for question, p2 for edges while (p1 <= m) { while (s[p2].r >= q[p1].k) { merge(s[p2].x, s[p2].y); p2++; } ans[q[p1].num] = siz[get(q[p1].v)] - 1; p1++; } for (int i = 1; i <= m; i++) printf("%d ", ans[i]); return 0; }
四.维护到根节点距离的并查集
根据具体问题,维护距离的方式会有所不同.
例如P1196 [NOI2002] 银河英雄传说中,如果把每个集合都看作一条链(即使路径压缩了,单调变化的权仍然可以体现这种关系),根据题意每次合并两个集合时,需要把一条链的头部接到另一条链的尾部,所以把新接上去的链的根节点权设为原链的大小,并把其父节点设为原链的根节点.(由于涉及到集合大小,需要额外地维护sz数组)
void merge(int x, int y) { x = get(x), y = get(y); fa[x] = y;
d[x] = sz[y]; // 注意这里 sz[y] += sz[x]; }
例如有两条链,1,4分别为根节点:(还没有进行路径压缩)
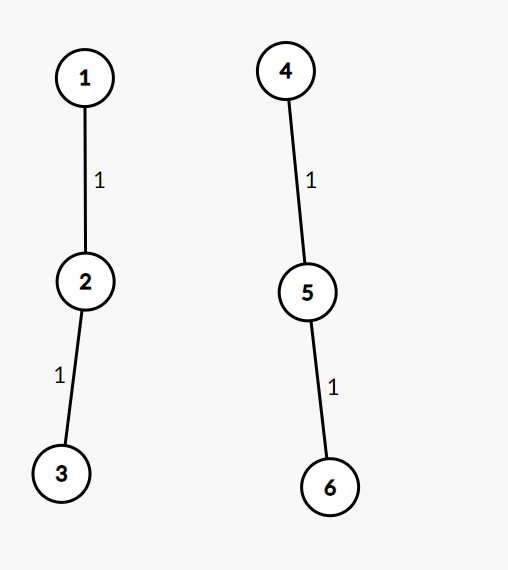 (边上的权表示一个节点到其父节点的距离)
(边上的权表示一个节点到其父节点的距离)
现在把右链接到左链尾部,即将4(右链的根节点)的父节点设为3(左链的尾端),新增的边的权(距离)是1.
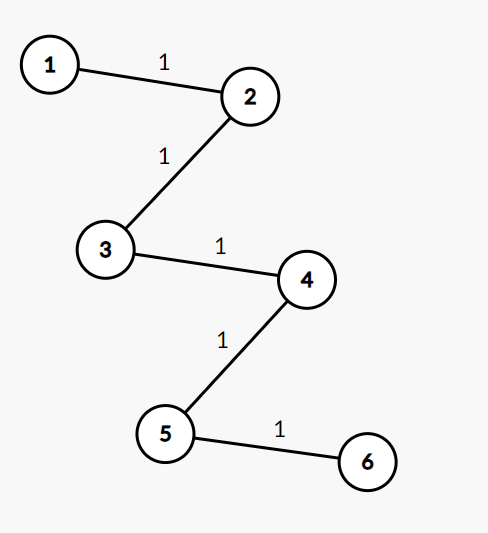
如果对4进行一次路径压缩:
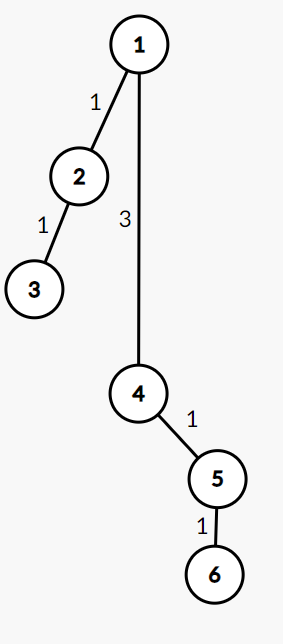
可以看出来这等效于把新接上去的链的根节点权设为原链的大小,并把其父节点设为原链的根节点.
注意,只需要更新右链的父节点权值即可,其子节点的权值会在路径压缩时正确地更新.d[x]只有在进行路径压缩(调用get(x))后才表示x与根节点之间的距离.
d[x] = sz[y] 就是这样得来的.根据题目要求也可以设计其它的更新方式.
get进行路径压缩时对应地要更新权.

#include <algorithm> #include <cstdio> #include <cstring> #include <cmath> #include <iostream> using namespace std; #define SIZE 30010 int fa[SIZE], d[SIZE], siz[SIZE], n; inline int read() { char ch = getchar(); int x = 0, f = 1; while (ch > '9' || ch < '0') { if (ch == '-') f = -1; ch = getchar(); } while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); } return x * f; } int get(int x) { if (x == fa[x]) return x; int root = get(fa[x]); d[x] += d[fa[x]]; return fa[x] = root; } void merge(int x, int y) { x = get(x), y = get(y); fa[x] = y, d[x] = siz[y]; siz[y] += siz[x]; } void init() { for (int i = 1; i <= SIZE; i++) { fa[i] = i; // d[i] = 1; siz[i] = 1; } } int main() { int t = read(), x, y; char ch; init(); while (t--) { cin >> ch; x = read(), y = read(); if (ch == 'M') merge(x, y); else{ int nx = get(x), ny = get(y); if(nx != ny) puts("-1"); else printf("%d ", abs(d[x] - d[y]) - 1); } } return 0; }
(图片由https://csacademy.com/app/graph_editor/生成)
五.维护更复杂的带权边并查集
由上文可见,边带权可以维护的信息有到根节点的距离,所在集合的大小,如果适当处理还可以维护其它信息.
始终牢记,带权边中的边,权指的是一个点到其父节点(不一定是根节点)的关系.调用get时的路径压缩会更新边和权,这个"权"的含义完全是根据题意自行定义的,更新的方式根据其意义编写.
再以P2024 [NOI2001] 食物链为例,如果使用带权边并查集,对应的merge和get要重写.不变的是这个"权"总是指某节点与其根节点的某种关系.
在这题中,权代表循环食物链中的三个成员,用0,1,2表示,在此基础上进行处理.(本质上是在维护对3取模的距离,并且合并两集合时也有了特殊的限制条件:使得给定的两点间的距离有着指定的关系)
注意这里的两种merge:
void merge1(int x, int y) { // same d[fa[x]] = (d[y] - d[x] + 3) % 3; fa[fa[x]] = fa[y]; } void merge2(int x, int y) { // x eat y d[fa[x]] = (d[y] - d[x] + 4) % 3; fa[fa[x]] = fa[y]; }
(由于merge前已经对x,y进行了路径压缩,fa[x],fa[y]就是x,y的根节点)
这里不能像平常一样令x=get(x),因为这里仍然需要使用原先的d[x]和d[y]的关系.
