P1314 [NOIP2011 提高组] 聪明的质监员

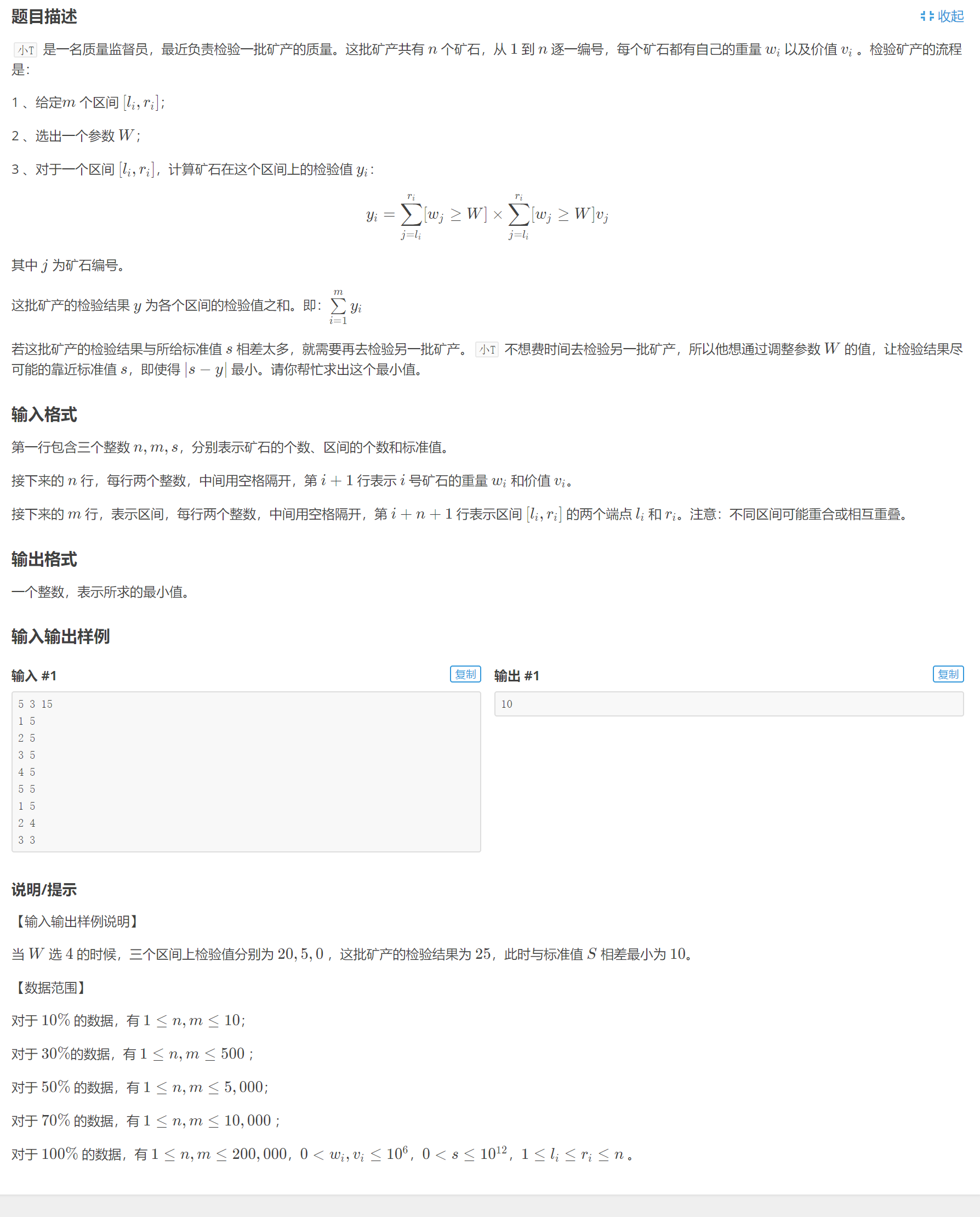
 数据范围只允许O(nlogn)的复杂度,由于答案显然具有单调性,使用二分,那么就要有O(n)算法来写check函数.

起初这对于我很有迷惑性,虽然知道这些区间要用前缀和来查询,却没注意到把求前缀和的过程放到check函数里,而不是预先算出所有情况下的前缀和,就可以保证复杂度了.

牢记计算前缀和的过程仅仅是O(n),所以这题完全可以随每次check时随用随算,这个开销并不会增大复杂度.

long long check(long long x) {  // return y
    for (int i = 1; i <= n; i++) {
        cts[i] = cts[i - 1] + (w[i] >= x);　　　　　　// (符合条件的)数量的前缀和
        vs[i] = vs[i - 1] + (w[i] >= x) * v[i];　　　// 价值的前缀和
    }
    long long sum = 0;
    for (int i = 1; i <= m; i++)
        sum += (cts[r[i]] - cts[l[i] - 1]) * (vs[r[i]] - vs[l[i] - 1]);
    return sum;
}

此外,注意要求出使|s-y|最小的y,这并不是可不可行的问题,所以check不是简单的bool返回值的函数,而是返回给定w得到的y的值,据此再进行操作.

而即使知道了y,也只能进行有限的判断:(注意y随着w的递增而递减,假设check(w₀)=y)

若s-y>0,则y的值不应该取更小,也就是w的取值不应该大于w₀,即w的右边界(含)为w₀.

若s-y<=0,则y的值不应该取更大,也就是w的取值不应该小于w₀,即w的左边界(含)为w₀.

根据这些判断最终是不一定会得到一个L=R的解的.

把限制条件设为L<R-1,则结束循环时L=R-1(也有可能是L=R),这里的R对应s-y>0边界内侧的第一个值,同时L对应s-y<=0边界内侧的第一个值.

此时简单判断一下两者谁更优即可.

如果想要在二分的过程中直接求解出最优解也是可行的,不过这里的二分写法不很容易适应,实现起来可能也更困难.

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <cmath>
using namespace std;

int n, m, w[200010], v[200010], l[200010], r[200010];
long long cts[200010], vs[200010];
long long s, ans = 1e13;

long long check(long long x) {  // return y
    for (int i = 1; i <= n; i++) {
        cts[i] = cts[i - 1] + (w[i] >= x);
        vs[i] = vs[i - 1] + (w[i] >= x) * v[i];
    }
    long long sum = 0;
    for (int i = 1; i <= m; i++)
        sum += (cts[r[i]] - cts[l[i] - 1]) * (vs[r[i]] - vs[l[i] - 1]);
    return sum;
}

int main() {
    scanf("%d%d%lld", &n, &m, &s);
    for (int i = 1; i <= n; i++) scanf("%d%d", w + i, v + i);
    for (int i = 1; i <= m; i++) scanf("%d%d", l + i, r + i);

    long long L = 0, R = 1e13;
    while (L < R - 1) {
        long long mid = L + R >> 1;
        long long y = check(mid);
        if (s - y > 0)
            R = mid;
        else
            L = mid;
    }

    printf("%lld
", min(abs(check(L) - s), abs(check(R) - s)));

    return 0;
}