动态规划入门笔记

一.背包问题

先上两个问题吧,可以把它们当作模板用,题解就不写了.

只需要找到自己最容易理解的方法就行了,不需要花时间钻研书上的各种不同的递推公式.

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;

long long W, m, dp[10000010];
int t[10010], v[10010];

int main(){
    cin >> W >> m;
    for(int i = 0; i < m; i++) cin >> t[i] >> v[i];

    for(int i = 0; i < m; i++)
        for(int j = 0; j <= W; j++)
            if(j >= t[i])
                dp[j] = max(dp[j], dp[j - t[i]] + v[i]);

    cout << dp[W] << endl;

    return 0;
}

倒推的代码可以忽略掉(而且我发现因为编辑失误那段折叠的代码没法展开了,正合我意),我觉得这是十分反人类的做法.

背包问题我觉得最容易理解的想法是在dp[i][j]记录在前i个物品中总重量不超过j的最大总价值.见下面的01背包做法:

此外,书上还列举了一堆等价的递推方法,忘掉那些东西,会这一套就行了.

---

再说说这个完全背包的题吧.

好好看书就知道应该这样写,递推式看书就知道怎么来的了,这里记住结论:

但是这题的数据范围会直接爆掉二维数组,所以得用数组再利用(因而只需要一维数组)的做法,如开头的代码所示.

---

使用一维数组处理这两个问题:

(比开头的代码在j初始化的地方做得更好)

注意这里的覆盖操作为什么是正确的:

　　首先,j < w[i]的部分,数组的值没有改变,即if(j < w[i]) dp[i + 1][j] = dp[i][j],参考上上张图.

　　然后,j >= w[i]的部分等价于dp[i + 1][j] = max(dp[i][j], dp[i][j - w[i]] + v[i]).

　　从而得知这是与二维数组做法完全等价的.

会发现这里的j是从W循环到w[i],这也是和完全背包代码唯一有区别的地方.同样是降维,却产生了一个细节差异,一开始这是让人十分困惑的.

调试了一下发现这里是为了防止重复选择同一物品的情况发生.

考虑如下数据:

70 3
71 100
69 1
1 2

完全背包求解:140　　　　(取70个3号物品)

观察到:

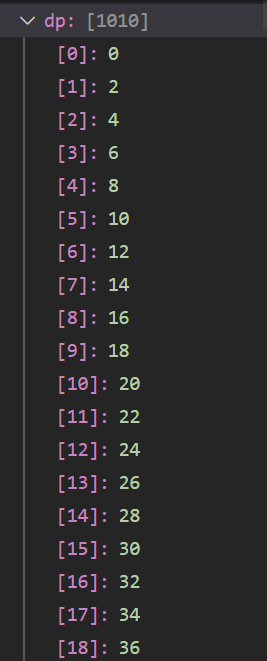
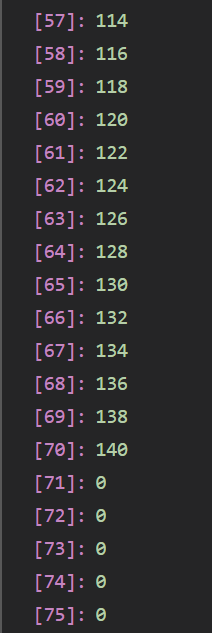
这里就可以明显看出来为什么01背包不适用于j从0到W的循环了,我们本希望避免已经选择的物品,但是这种循环的覆盖情况并不支持.(自行想象并加以理解)

01背包求解:3　　　　　　(取二号和三号物品)

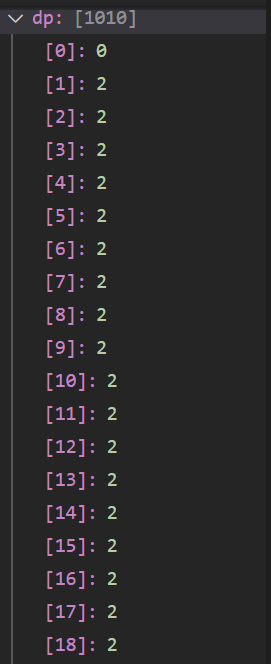
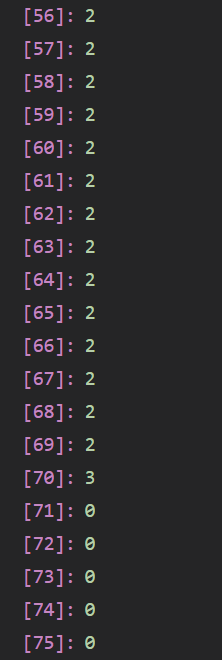
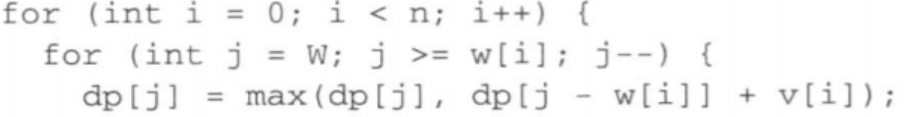
 结合这段代码仔细思考.

你会得出,对于j的每一个状态,j-w[i]的状态总是没有取物品i的.(因为i的循环使得i递增)

十分玄妙,但是说到这里已经足够理解了.

补充:

　　多重背包

　　滚动数组(一种技巧)

---

书上还提到了LCS,可以理解但是等用到的时候再去学.

持续更新中.