题目描述
设d(x)为x的约数个数,给定N、M,求 

输入
输入文件包含多组测试数据。
第一行,一个整数T,表示测试数据的组数。
接下来的T行,每行两个整数N、M。
输出
T行,每行一个整数,表示你所求的答案。
样例输入
2
7 4
5 6
样例输出
110
121
题解
莫比乌斯反演
根据 bzoj4176 推出的结论,![]()
那么就有:
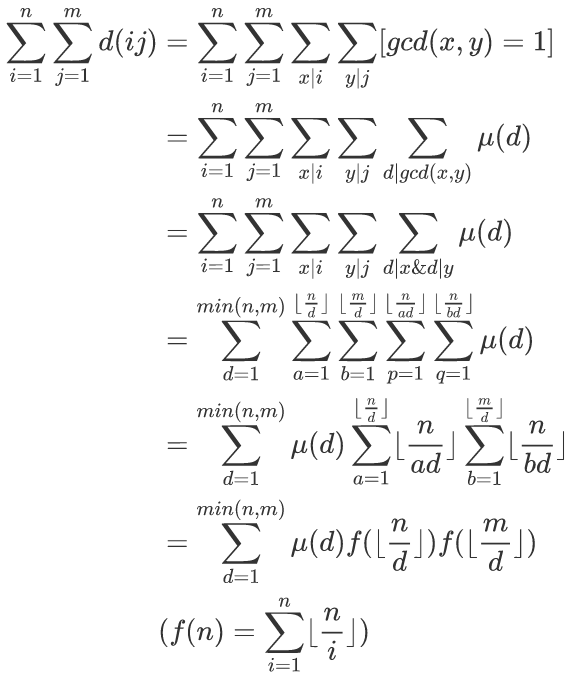
预处理mu及其前缀和。
由于要处理多组询问,所以需要用O(n√n)的时间预处理出f,然后对于每组询问分块来求。
#include <cstdio>
#include <algorithm>
#define N 50010
using namespace std;
typedef long long ll;
const int n = 50000;
int mu[N] , sum[N] , prime[N] , tot , f[N];
bool np[N];
ll cal(int a , int b)
{
int i , last;
ll ans = 0;
for(i = 1 ; i <= a && i <= b ; i = last + 1) last = min(a / (a / i) , b / (b / i)) , ans += (ll)(sum[last] - sum[i - 1]) * f[a / i] * f[b / i];
return ans;
}
int main()
{
int i , j , last , T , a , b;
mu[1] = sum[1] = 1;
for(i = 2 ; i <= n ; i ++ )
{
if(!np[i]) mu[i] = -1 , prime[++tot] = i;
for(j = 1 ; j <= tot && i * prime[j] <= n ; j ++ )
{
np[i * prime[j]] = 1;
if(i % prime[j] == 0)
{
mu[i * prime[j]] = 0;
break;
}
else mu[i * prime[j]] = -mu[i];
}
sum[i] = sum[i - 1] + mu[i];
}
for(i = 1 ; i <= n ; i ++ )
for(j = 1 ; j <= i ; j = last + 1)
last = i / (i / j) , f[i] += (last - j + 1) * (i / j);
scanf("%d" , &T);
while(T -- ) scanf("%d%d" , &a , &b) , printf("%lld
" , cal(a , b));
return 0;
}