Chessboard
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 12800 | Accepted: 4000 |
Description
Alice and Bob often play games on chessboard. One day, Alice draws a board with size M * N. She wants Bob to use a lot of cards with size 1 * 2 to cover the board. However, she thinks it too easy to bob, so she makes some holes on the board (as shown in the figure below).
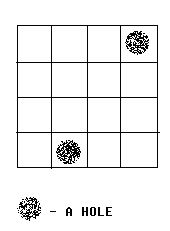
We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below:
1. Any normal grid should be covered with exactly one card.
2. One card should cover exactly 2 normal adjacent grids.
Some examples are given in the figures below:
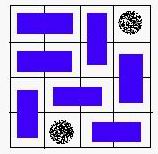
A VALID solution.
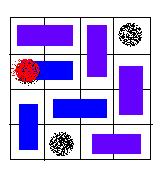
An invalid solution, because the hole of red color is covered with a card.
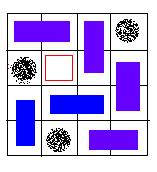
An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.

We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below:
1. Any normal grid should be covered with exactly one card.
2. One card should cover exactly 2 normal adjacent grids.
Some examples are given in the figures below:

A VALID solution.

An invalid solution, because the hole of red color is covered with a card.

An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.
Input
There are 3 integers in the first line: m, n, k (0 < m, n <= 32, 0 <= K < m * n), the number of rows, column and holes. In the next k lines, there is a pair of integers (x, y) in each line, which represents a hole in the y-th row, the x-th column.
Output
If the board can be covered, output "YES". Otherwise, output "NO".
Sample Input
4 3 2 2 1 3 3
Sample Output
YES
Hint
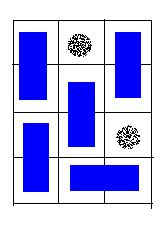
A possible solution for the sample input.
Source
POJ Monthly,charlescpp
和 hdu 1507类似,构无向图然后判断匹配数是否等于合法的格数。
心算32*32错了= = RE了两次,开始以为32*32是90+,第二次以为是900+,笔算后才知道是1024..
1 //224K 125MS C++ 1731B 2014-06-10 12:44:41 2 #include<iostream> 3 #include<vector> 4 #define N 1050 5 using namespace std; 6 vector<int>V[N]; 7 int match[N]; 8 int vis[N]; 9 int g[35][35]; 10 int dfs(int u) 11 { 12 for(int i=0;i<V[u].size();i++){ 13 int v=V[u][i]; 14 if(!vis[v]){ 15 vis[v]=1; 16 if(match[v]==-1 || dfs(match[v])){ 17 match[v]=u; 18 return 1; 19 } 20 } 21 } 22 return 0; 23 } 24 int hungary(int n) 25 { 26 int ret=0; 27 memset(match,-1,sizeof(match)); 28 for(int i=1;i<=n;i++){ 29 memset(vis,0,sizeof(vis)); 30 ret+=dfs(i); 31 } 32 return ret; 33 } 34 int main(void) 35 { 36 int n,m,k,x,y; 37 while(scanf("%d%d%d",&n,&m,&k)!=EOF) 38 { 39 memset(g,0,sizeof(g)); 40 for(int i=0;i<N;i++) V[i].clear(); 41 for(int i=0;i<k;i++){ 42 scanf("%d%d",&y,&x); 43 g[x-1][y]=1; 44 } 45 int map[N]={0},pos=0; 46 for(int i=0;i<n;i++) 47 for(int j=1;j<=m;j++) 48 if(!g[i][j]){ 49 if(!map[i*m+j]) map[i*m+j]=++pos; 50 int u=map[i*m+j]; 51 if(j<m && !g[i][j+1]){ 52 if(!map[i*m+j+1]) map[i*m+j+1]=++pos; 53 V[u].push_back(map[i*m+j+1]); 54 V[map[i*m+j+1]].push_back(u); 55 } 56 if(i<n-1 && !g[i+1][j]){ 57 if(!map[(i+1)*m+j]) map[(i+1)*m+j]=++pos; 58 V[u].push_back(map[(i+1)*m+j]); 59 V[map[(i+1)*m+j]].push_back(u); 60 } 61 } 62 //printf("%d ",pos); 63 if(hungary(pos)==pos) puts("YES"); 64 else puts("NO"); 65 } 66 return 0; 67 }