Flow Problem
Time Limit: 5000/5000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 6674 Accepted Submission(s): 3112
Problem Description
Network flow is a well-known difficult problem for ACMers. Given a graph, your task is to find out the maximum flow for the weighted directed graph.
Input
The first line of input contains an integer T, denoting the number of test cases.
For each test case, the first line contains two integers N and M, denoting the number of vertexes and edges in the graph. (2 <= N <= 15, 0 <= M <= 1000)
Next M lines, each line contains three integers X, Y and C, there is an edge from X to Y and the capacity of it is C. (1 <= X, Y <= N, 1 <= C <= 1000)
For each test case, the first line contains two integers N and M, denoting the number of vertexes and edges in the graph. (2 <= N <= 15, 0 <= M <= 1000)
Next M lines, each line contains three integers X, Y and C, there is an edge from X to Y and the capacity of it is C. (1 <= X, Y <= N, 1 <= C <= 1000)
Output
For each test cases, you should output the maximum flow from source 1 to sink N.
Sample Input
2
3 2
1 2 1
2 3 1
3 3
1 2 1
2 3 1
1 3 1
Sample Output
Case 1: 1
Case 2: 2
Author
HyperHexagon
Source
Recommend
一个证明需要反向更新的例子:
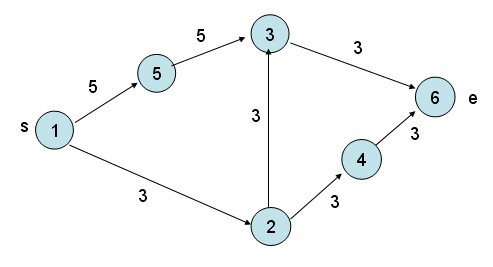
这个图从1到6明显最的流量为3+3=6,但如果不用反向更新,由于用BFS首先找到一条路径1-2-3-6,然后1-2,2-3,3-6这几条边被更新成了0,就再也找不到增广路径到6了,而1-5-3的剩余的5个流量就无路可走了,用反向更新会再在3-2这里加一条流量为3的边,这时候1-5-3的5流量就可以通过这条边到2再到4再到6了,这就是反向更新的需要。
参考:http://blog.csdn.net/huanglianzheng/article/details/5754057
网络最大流入门模板题:
ford fulkerson 标号法:
1 //750MS 4216K 1444 B C++ 2 #include<iostream> 3 #include<queue> 4 #define INF 0x7ffffff 5 #define N 1005 6 using namespace std; 7 int g[N][N],flow[N]; //记录流量fij, 和每次的调整值flow[e] 8 int father[N],vis[N]; //记录父节点 和 标记已遍历节点 9 int maxflow,n,m; 10 inline int Min(int a,int b) 11 { 12 return a<b?a:b; 13 } 14 void ford_fulkerson(int s,int e) 15 { 16 queue<int>Q; 17 maxflow=0; 18 while(1){ //调整到无增广链为止 19 memset(flow,0,sizeof(flow)); 20 memset(vis,0,sizeof(vis)); 21 flow[s]=INF; 22 Q.push(s); 23 while(!Q.empty()){ 24 int u=Q.front(); 25 Q.pop(); 26 for(int v=1;v<=n;v++){ 27 if(!vis[v] && g[u][v]>0){ 28 vis[v]=1; 29 father[v]=u; 30 Q.push(v); 31 flow[v]=Min(flow[u],g[u][v]); 32 } 33 } 34 if(flow[e]>0){ 35 while(!Q.empty()) Q.pop(); 36 break; 37 } 38 } 39 if(flow[e]==0) break; 40 for(int i=e;i!=s;i=father[i]){ 41 g[father[i]][i]-=flow[e]; 42 g[i][father[i]]+=flow[e]; 43 } 44 maxflow+=flow[e]; 45 } 46 } 47 int main(void) 48 { 49 int t,k=1; 50 int a,b,c; 51 scanf("%d",&t); 52 while(t--) 53 { 54 scanf("%d%d",&n,&m); 55 memset(g,0,sizeof(g)); 56 for(int i=0;i<m;i++){ 57 scanf("%d%d%d",&a,&b,&c); 58 g[a][b]+=c; 59 } 60 ford_fulkerson(1,n); 61 printf("Case %d: %d ",k++,maxflow); 62 } 63 return 0; 64 }