Is It A Tree?
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 12108 Accepted Submission(s): 2757
Problem Description
A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.
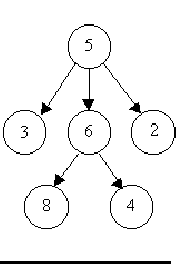
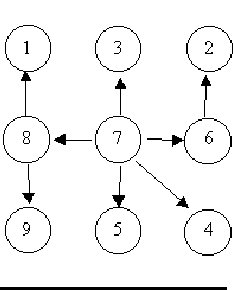
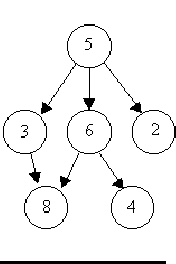
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.



In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
Input
The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.
Output
For each test case display the line ``Case k is a tree." or the line ``Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).
Sample Input
6 8 5 3 5 2 6 4
5 6 0 0
8 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 0
3 8 6 8 6 4
5 3 5 6 5 2 0 0
-1 -1
Sample Output
Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.
Source
Recommend
1 //15MS 1516K 1207 B G++ 2 /* 3 4 题意: 5 给出若干对数字,前一个为后一个的父节点,结合所有给出的情况 6 判断其是否组成一棵树。 7 树的定义: 8 1、有且只有一个根节点(没有父节点的点) 9 2、每个节点只有一个父节点 10 3、 从根节点到任何一节点只有一条路径 11 12 并查集+STL: 13 直接把数组开大会MLE,一开始我就是这样的,一直MLE或RE, 14 故要使用STL节省数组开销,感觉这题应该还有更简单的解法,不过 15 题意目的是要练习并查集,故用并查集的解法。 16 17 */ 18 #include<iostream> 19 #include<map> 20 using namespace std; 21 map<int,int>M; 22 int set[100005]={0}; 23 int root[100005]={0}; 24 int vis[100005]={0}; 25 int find(int x) 26 { 27 if(x==set[x]) return x; 28 return find(set[x]); 29 } 30 void merge(int a,int b) 31 { 32 set[find(b)]=find(a); 33 } 34 int main(void) 35 { 36 int a,b; 37 int n=1,k=1; 38 int flag=0; 39 while(scanf("%d%d",&a,&b)!=EOF) 40 { 41 if(a==-1 && b==-1) break; 42 if(a==0 && b==0){ 43 int cnt=0; 44 for(int i=1;i<n;i++) 45 if(root[i]==0) cnt++; //条件1,只有一颗树 46 if(cnt>1) flag=1; 47 cnt=find(1); 48 for(int i=2;i<n;i++) 49 if(find(i)!=cnt) flag=1; //条件1 50 if(flag) printf("Case %d is not a tree. ",k++); 51 else printf("Case %d is a tree. ",k++); 52 n=1;flag=0; 53 M.clear(); 54 memset(set,0,sizeof(set)); 55 memset(vis,0,sizeof(vis)); 56 memset(root,0,sizeof(root)); 57 continue; 58 } 59 if(M[a]==0) M[a]=n++; 60 if(M[b]==0) M[b]=n++; 61 if(root[M[b]]!=0) flag=1; //条件2、3 62 root[M[b]]=M[a]; 63 vis[M[a]]=vis[M[b]]=1; 64 merge(M[a],M[b]); 65 } 66 return 0; 67 }