【2021夏纪中游记】2021.7.13模拟赛

2021.7.13模拟赛

比赛概括：

(mathrm{sum}=20+0+0+20)

唉。

T1 消息传递：

题目大意：

一个点在某一秒可向相邻节点扩散，问哪些节点开始扩散能最快多少秒将所有节点全部覆盖。

思路：

谢谢各位，我把学的东西都忘了。

先想暴力，对于每个点求出 (f_i) 表示从以 (i) 为根的子树中扩散到 (i)，最长花费的时间。则有：

[f_u=max_{vinmathrm{son}(x)}{f_v+mathrm{order}_v} ]

其中 (mathrm{order}_v) 表示 (u) 扩散到 (v) 的顺序，可以贪心排序求出。然后每个点都作为根算一遍，时间复杂度 (mathcal{O}(n^2log n))。

但是如果暴力算法，很多状态都重复算了：

如图，两个灰点作根，与深灰点的 (f_i) 无关。

则设 (g_i) 表示从以 (i) 为根的子树外扩散到 (i)，最长花费的时间：

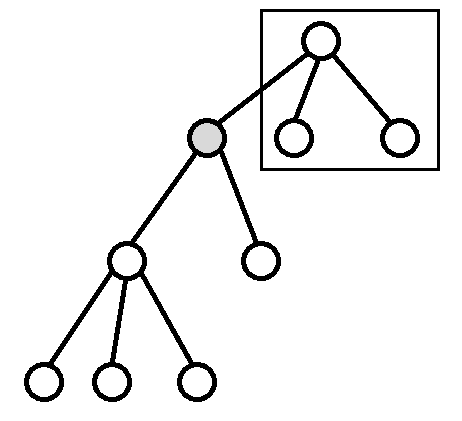
如图，黑框内则表示为灰点的 (g_i)。则有：

[g_u=max_{k=mathrm{fa}(x)}(g_k+mathrm{order}_k,max_{vinmathrm{son}(k),v e u}{f_v+mathrm{order}_v}) ]

实现时建议由当前节点推出子节点的 (g_i)。

统计答案时就在排 (mathrm{order}_i) 时顺便找到最大的即可。

代码：

const int N = 2e5 + 10;

inline ll Read()
{
	ll x = 0, f = 1;
	char c = getchar();
	while (c != '-' && (c < '0' || c > '9')) c = getchar();
	if (c == '-') f = -f, c = getchar();
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
	return x * f;
}

int n;

struct edge
{
	int to, nxt;
}e[N << 1];
int head[N], tot;
void add(int u, int v)
{
	e[++tot] = (edge) {v, head[u]}, head[u] = tot;
}

bool cmp(int a, int b)
{
	return a > b;
}

int f[N], g[N];
void dfs(int u, int fa)
{
	vector <int> son;
	for (int i = head[u]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == fa) continue;
		dfs(v, u);
		son.push_back(f[v]);
	}
	sort (son.begin(), son.end(), cmp);
	for (int i = 0; i < son.size(); i++)
		f[u] = max(f[u], son[i] + i + 1);
	return ;
}
int t[N];
struct node
{
	int l, r;
}Max[N];
int Ans[N], cnt, ans = 1e9;

void ChangeRoot(int u, int fa)
{
	vector <int> son;
	for (int i = head[u]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == fa) continue;
		son.push_back(f[v]);
	}
	if (fa) son.push_back(g[u]) ;
	sort (son.begin(), son.end(), cmp);
	for (int i = 0; i < son.size(); i++)
		t[i] = son[i] + i + 1;
	Max[0].l = t[0], Max[son.size() - 1].r = t[son.size() - 1];
	for (int i = 1; i < son.size(); i++)
		Max[i].l = max(Max[i - 1].l, t[i]);
	for (int i = son.size() - 2; ~i; i--)
		Max[i].r = max(Max[i + 1].r, t[i]);
	reverse(son.begin(), son.end());
	for (int i = head[u]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == fa) continue;
		int x = lower_bound(son.begin(), son.end(), f[v]) - son.begin();
		x = son.size() - x - 1;
		g[v] = max(x == 0? 0: Max[x - 1].l, x == son.size() - 1? 0: Max[x + 1].r - 1);
	}
	Ans[u] = Max[son.size() - 1].l;
	for (int i = head[u]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if (v == fa) continue;
		ChangeRoot(v, u);
	}
}

int main()
{
	freopen("news.in", "r", stdin);
	freopen("news.out", "w", stdout);
	n = Read();
	for (int i = 2, v; i <= n; i++)
		v = Read(), add(v, i), add(i, v);
	dfs(1, 0);
	ChangeRoot(1, 0);
	for (int i = 1; i <= n; i++)
		ans = min(ans, Ans[i]);
	printf ("%d
", ans + 1);
	for (int i = 1; i <= n; i++)
		if (Ans[i] == ans) printf ("%d ", i);
	return 0;
}

T2 JIH的玩偶：

题目大意：

每次求在一棵树上的最大值与最小值的差，且最大值必须是最小值的祖先。

思路：

考场没读懂最大最小值的先后顺序。

其实是一道简单树上倍增。设 (f_{i,j},mathrm{Max}_{i,j},mathrm{Min}_{i,j},mathrm{Ans}_{i,j}) 分别表示 (i) 节点向上走 (2^j) 的节点、区间最大、区间最小、区间合法大小差。

转移见代码。

代码：

const int N = 200010, M = 30;

inline ll Read()
{
	ll x = 0, f = 1;
	char c = getchar();
	while (c != '-' && (c < '0' || c > '9')) c = getchar();
	if (c == '-') f = -f, c = getchar();
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
	return x * f;
}

int n;
int f[N][M], mx[N][M], mn[N][M], Ans[N][M];

int main()
{
	freopen("tree.in", "r", stdin);
	freopen("tree.out", "w", stdout);
	n = Read();
	int m = log2(n) + 1;
	mn[0][0] = 1e9;
	for (int i = 1; i <= n; i++)
		mx[i][0] = mn[i][0] = Read();
	for (int i = 1; i < n; i++)
	{
		int x = Read(), fa = Read();
		f[x][0] = fa;
	}
	for (int j = 1; j <= m; j++)
		for (int i = 1; i <= n; i++)
		{
			f[i][j] = f[f[i][j-1]][j - 1];
			mx[i][j] = max(mx[i][j - 1], mx[f[i][j-1]][j - 1]);
			mn[i][j] = min(mn[i][j - 1], mn[f[i][j-1]][j - 1]);
			Ans[i][j] = max(max(Ans[i][j - 1], Ans[f[i][j-1]][j - 1]), max(0, mx[f[i][j-1]][j - 1] - mn[i][j - 1]));
		} 
	for (int t = Read(); t--; )
	{
		int u = Read(), k = Read(), ans = 0, Min = 1e9;
		for (int j = 0; k; j++, k >>= 1)
			if (k & 1)
			{
				ans = max(ans, max(Ans[u][j], mx[u][j] - Min));
				Min = min(Min, mn[u][j]);
				u = f[u][j];
			}
		printf ("%d
", ans);
	}
	return 0;
}

T3 摘取作物：

题目大意：

在 (n imes m) 的地图中，点 ((i,j)) 的权值为 (w_{i,j})。若每行每列都不超过 (2) 个，求最大选择权值是多少。

正文：

最大费用流经典题。新建 (S) 连向每行（容量 (2)，费用 (0)），每行连向每列（容量 (1)，费用 (a_{i,j})），每列连向 (T)（容量 (2)，费用 (0)）。

代码：

const int M = 200010, N = 10010;

inline ll Read()
{
	ll x = 0, f = 1;
	char c = getchar();
	while (c != '-' && (c < '0' || c > '9')) c = getchar();
	if (c == '-') f = -f, c = getchar();
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
	return x * f;
}

int n, m, s, t, tot;
struct edge
{
	int x, y, w, z, op, next;
} e[M];
int head[N];

void Add(int x, int y, int w, int z)
{
	e[++tot] = (edge){x, y, w, z, tot + 1, head[x]}; 
	head[x] = tot;
	e[++tot] = (edge){y, x, 0, -z, tot - 1, head[y]}; 
	head[y] = tot; 
}

int dis[N], incf[N], pre[N];
bool vis[N];
queue <int> que;

bool spfa()
{
	while(!que.empty())que.pop();
	memset(dis, -127 / 3, sizeof(dis));
	memset(vis, 0, sizeof(vis));
	dis[s] = 0;
	que.push(s);
	vis[s] = 1;
	while(!que.empty())
	{
		int x = que.front();que.pop();vis[x] = 0;
		for (int i = head[x]; i; i = e[i].next)
		{
			int y = e[i].y;
			if(dis[y] < dis[x] + e[i].z && e[i].w)
			{
				dis[y] = dis[x] + e[i].z;
				pre[y] = i;
				if(!vis[y]) vis[y] = 1, que.push(y);
			}
		}
	}
	return dis[t] > 0;
}

int maxflow, mincost;

int MCMF()
{
	int ans = 0;
	while(spfa())
	{
		int mx = n;
		for (int i = pre[t]; i; i = pre[e[i].x]) mx = min(mx, e[i].w);
		for (int i = pre[t]; i; i = pre[e[i].x]) 
			e[i].w -= mx, e[e[i].op].w += mx;
		ans += mx * dis[t];
	}
	return ans;
}

int main()
{
	freopen("pick.in", "r", stdin);
	freopen("pick.out", "w", stdout);
	n = Read(), m = Read(); s = n + m + 1, t = n + m + 2;
	for (int i = 1; i <= n; i++) Add(s, i, 2, 0);
	for (int i = 1; i <= m; i++) Add(i + n, t, 2, 0);
	for (int i = 1; i <= n; i++)
		for (int j = 1, w; j <= m; j++)
			w = Read(), Add(i, j + n, 1, w);
	printf("%d
", MCMF());
	return 0;
}

T4 公路维护：

题目大意：

我们知道，每天都有成千上万的车辆在高速公路上行驶。如果一辆装有若干吨货物的卡车通过一段高速公路，就会对这段公路造成一定程度的破坏。

整段高速公路有一个初始的耐久度I。如果一辆装有d吨货物的卡车通过一段高速公路，这段公路的耐久度就会减少d。一旦某段公路的耐久度小于或等于0，这段公路就会永久性地毁坏。卡车无法通过已经毁坏的地方。

有两种维护公路的车辆：T1和T2。T1车可以将一段公路的耐久度增加r。T2车可以将一段公路的耐久度小于p的部分修复至p。虽然维护公路的车辆可以通过已经毁坏的部分，但是已经毁坏的地方仍然无法修复。

你的任务是统计一下一共有多少辆卡车可以成功通行。

正文：

线段树，如果有坏的点就暴力处理，因为每个点最多坏一次。

代码：

const int N = 1e5 + 10;

inline ll Read()
{
	ll x = 0, f = 1;
	char c = getchar();
	while (c != '-' && (c < '0' || c > '9')) c = getchar();
	if (c == '-') f = -f, c = getchar();
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
	return x * f;
}

int n, m, Val;

struct Segment
{
	struct tree
	{
		int l, r;
		ll Min, Max, lzy1, lzy2;
	}t[N << 2];
	
	void Build(int l, int r, int p)
	{
		t[p].l = l, t[p].r = r, t[p].lzy1 = -1;
		if (l == r)
		{
			t[p].Min = t[p].Max = Val;
			return;
		}
		int mid = l + r >> 1;
		Build (l, mid, p << 1);
		Build (mid + 1, r, p << 1 | 1);
		t[p].Min = min(t[p << 1].Min, t[p << 1 | 1].Min);
		t[p].Max = max(t[p << 1].Max, t[p << 1 | 1].Max);
	}
	
	void Spread(int p)
	{
		if (~t[p].lzy1)
		{
			t[p << 1].Min = t[p << 1].Max = t[p << 1 | 1].Min = t[p << 1 | 1].Max = t[p].lzy1;
			t[p << 1].lzy1 = t[p << 1 | 1].lzy1 = t[p].lzy1;
			t[p << 1].lzy2 = t[p << 1 | 1].lzy2 = 0;
			t[p].lzy1 = -1;
		}
		if (t[p].lzy2)
		{
			t[p << 1].Min += t[p].lzy2, t[p << 1].Max += t[p].lzy2, 
			t[p << 1 | 1].Min += t[p].lzy2, t[p << 1 | 1].Max += t[p].lzy2;
			t[p << 1].lzy2 += t[p].lzy2, t[p << 1 | 1].lzy2 += t[p].lzy2;
			t[p].lzy2 = 0;
		}
	}
	
	void Sub(int l, int r, int p, int val)
	{
		if (l <= t[p].l && t[p].r <= r)
		{
			if (!t[p].Max) return;
			if (t[p].Max <= val) {t[p].Max = t[p].Min = t[p].lzy1 = t[p].lzy2 = 0; return;}
			if (t[p].Min > val) {t[p].Max -= val, t[p].Min -= val, t[p].lzy2 -= val; return;}
		}
		Spread(p);
		int mid = t[p].l + t[p].r >> 1;
		if (l <= mid) Sub(l, r, p << 1, val);
		if (mid < r) Sub(l, r, p << 1 | 1, val);
		t[p].Min = min(t[p << 1].Min, t[p << 1 | 1].Min);
		t[p].Max = max(t[p << 1].Max, t[p << 1 | 1].Max);
	}
	
	void Add(int l, int r, int p, int val)
	{
		if (l <= t[p].l && t[p].r <= r)
		{
			if (!t[p].Max) return;
			if (t[p].Min) {t[p].Max += val, t[p].Min += val, t[p].lzy2 += val; return;}
		}
		Spread(p);
		int mid = t[p].l + t[p].r >> 1;
		if (l <= mid) Add(l, r, p << 1, val);
		if (mid < r) Add(l, r, p << 1 | 1, val);
		t[p].Min = min(t[p << 1].Min, t[p << 1 | 1].Min);
		t[p].Max = max(t[p << 1].Max, t[p << 1 | 1].Max);
	}
	
	void Modify(int l, int r, int p, ll val)
	{
		if (l <= t[p].l && t[p].r <= r)
		{
			if (!t[p].Max) return;
			if (t[p].Min)
			{
				if (t[p].Max <= val) {t[p].Max = t[p].Min = t[p].lzy1 = val; t[p].lzy2 = 0;return;}
				if (t[p].Min > val) return;
			}
		}
		Spread(p);
		int mid = t[p].l + t[p].r >> 1;
		if (l <= mid) Modify(l, r, p << 1, val);
		if (mid < r) Modify(l, r, p << 1 | 1, val);
		t[p].Min = min(t[p << 1].Min, t[p << 1 | 1].Min);
		t[p].Max = max(t[p << 1].Max, t[p << 1 | 1].Max);
	}
	
	ll Query(int l, int r, int p)
	{
		if (l <= t[p].l && t[p].r <= r)
			return t[p].Min;
		Spread(p);
		int mid = t[p].l + t[p].r >> 1;
		ll ans = 1e10;
		if (l <= mid) ans = min(ans, Query(l, r, p << 1));
		if (mid < r) ans = min(ans, Query(l, r, p << 1 | 1));
		return ans;
	}
}t;

int ans;

int main()
{ 
	freopen("road.in", "r", stdin);
	freopen("road.out", "w", stdout);
	n = Read(), m = Read(), Val = Read();
	t.Build(1, n, 1);
	while (m--)
	{
		int op = Read(), l = Read(), r = Read(), val = Read();
		if (op == 1)
		{
			if (t.Query(l, r, 1) > 0) ans++, t.Sub(l, r, 1, val);
		}
		if (op == 2) t.Add(l, r, 1, val);
		if (op == 3) t.Modify(l, r, 1, val);
	}
	printf ("%d
", ans);
	return 0;
}