题目大意:
求 (n) 个矩形的面积并。
正文:
本题计算面积并在扫描线中较为简单。抛开离散化,我们着重讲扫描线。
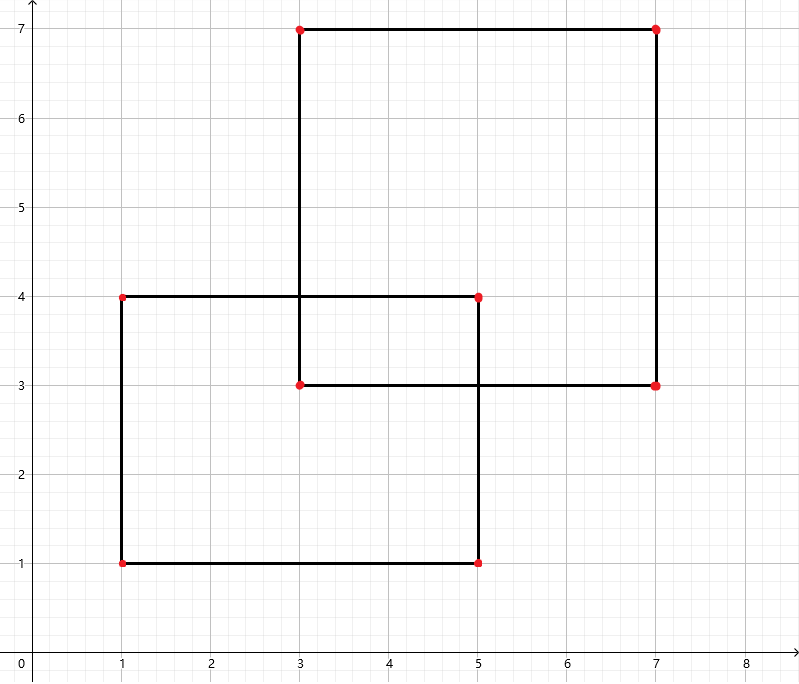
与上图为例,思考怎么计算它们的几何并。
暴力
用一个数组来存信息,覆盖了就标 1,否则标 0。暴力既好想又好写,但当坐标一大,时空都会超。
容斥
用总面积减去重合面积。但只局限于重合少的题。
分割图形
将图形重新分割成一个个规则的矩形,用线段树维护一条扫描的线。
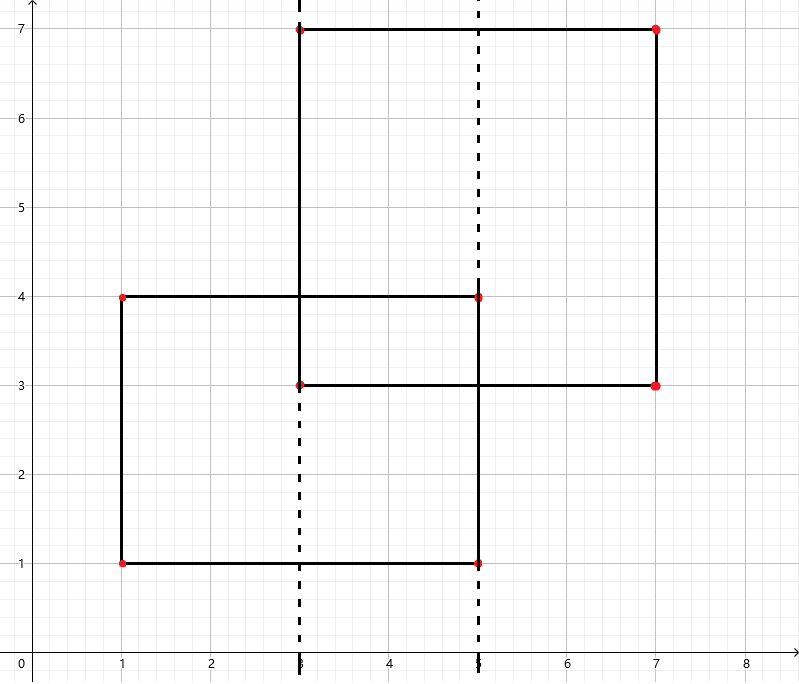
如上图,每扫描到一段,该段面积就是直线上覆盖的长度乘该段的宽度。
顺着这个思路来,用一个四元组 ((x,y_1,y_2,flag)) 记录每一条竖线,表示竖线的坐标及是否是左右边界。
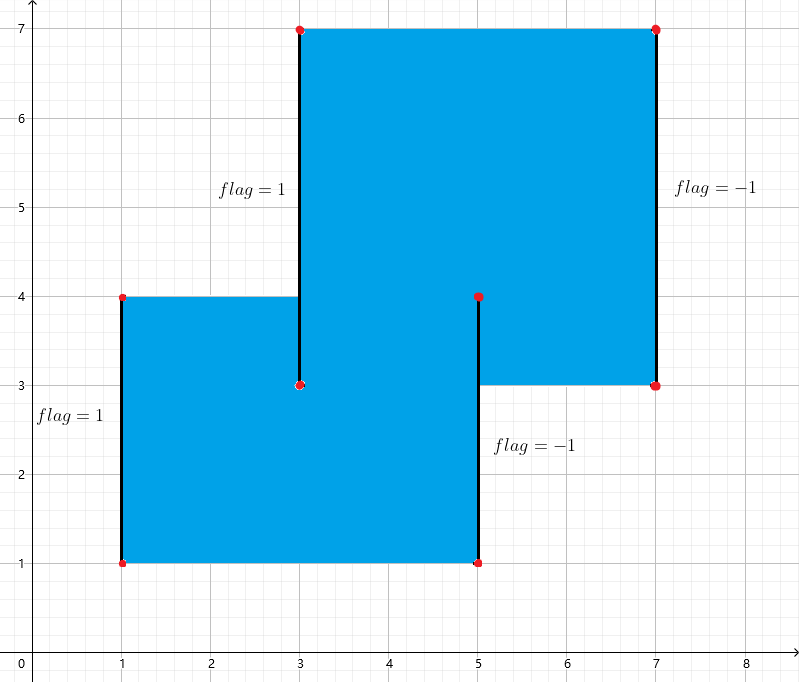
线段树维护扫描线上被覆盖的长度,每次修改后,更新被覆盖长度(如下)。
void pushup(int x)
{
if(t[x].cnt) t[x].len = disx[t[x].r + 1] - disx[t[x].l];
else t[x].len = t[x * 2].len + t[x * 2 + 1].len;
}
对于线段树的标记,这里引入 李煜东的《算法竞赛》,在本题我们只关心整个扫描线(线段树根节点)上被覆盖的长度。四元组又成对出现,所以线段树区间修改也是重复出现,这样就没必要下传延时标记,而采用更加简单的做法:在线段树每个节点上另加维护该节点代表的区间被矩形覆盖的长度 (len),该节点自身被覆盖的次数 (cnt)。对于一个四元组 ((x,y_1,y_2,flag)),在 ([val(y_1),val(y_2)-1]) 上执行区间修改。该区间被线段树划分成 (log N) 个节点,把这些节点的 (cnt) 都加 (k)。
对于线段树任意一个节点 ([l,r]),若 (cnt>0),则 (len) 就等于两子节点 (len) 之和。在一个节点 (cnt) 被修改,以及线段树传递信息时,我们都按照方法更新 (len) 值。根节点 (len) 值就是整个扫描线被覆盖的长度。
代码:
const int N = 2000000 + 10;
int n;
struct SegmentTree
{
int l, r;
ll cnt, len;
}t[N << 2];
ll x[N], disx[N], y[N];
struct node
{
ll xd, xu, y, flag;
}a[N << 2];
bool cmp(node a, node b)
{
if(a.y == b.y) return a.flag > b.flag;
return a.y < b.y;
}
void build(int x, int l, int r)
{
t[x].l = l, t[x].r = r;
if(l == r) return;
int mid = (t[x].l + t[x].r) / 2;
build(x * 2, l, mid);
build(x * 2 + 1, mid + 1, r);
}
void pushup(int x)
{
if(t[x].cnt) t[x].len = disx[t[x].r + 1] - disx[t[x].l];
else t[x].len = t[x * 2].len + t[x * 2 + 1].len;
}
void change(int x, int l, int r, ll k)
{
if(l <= t[x].l && t[x].r <= r)
{
t[x].cnt += k;
pushup(x);
return;
}
int mid = (t[x].l + t[x].r) / 2;
if(l <= mid) change(x * 2, l, r, k);
if(r > mid) change(x * 2 + 1, l, r, k);
pushup(x);
}
ll ans;
int main()
{
scanf("%d", &n);
int m = n * 2;
for (int i = 1; i <= n; i ++)
{
scanf("%lld%lld%lld%lld", &x[(i << 1) - 1], &y[(i << 1) - 1], &x[(i << 1)], &y[(i << 1)]);
a[(i << 1) - 1].xd = a[(i << 1)].xd = x[(i << 1) - 1];
a[(i << 1) - 1].xu = a[(i << 1)].xu = x[(i << 1)];
a[(i << 1) - 1].y = y[(i << 1) - 1];
a[(i << 1)].y = y[(i << 1)];
a[(i << 1) - 1].flag = 1;
a[(i << 1)].flag = -1;
}
sort(x + 1, x + 1 + m);
m = unique(x + 1, x + 1 + m) - (x + 1);
for (int i = 1; i <= n * 2; i++)
{
int p1 = lower_bound(x + 1, x + 1 + m, a[i].xd) - x,
p2 = lower_bound(x + 1, x + 1 + m, a[i].xu) - x;
disx[p1] = a[i].xd, disx[p2] = a[i].xu;
a[i].xd = p1;
a[i].xu = p2;
}
m = 2 * n;
build(1, 1, m);
sort(a + 1, a + 1 + m, cmp);
for (int i = 1; i <= m; i++)
{
change(1, a[i].xd, a[i].xu - 1, a[i].flag);
ans += t[1].len * (a[i + 1].y - a[i].y);
}
printf("%lld
", ans);
return 0;
}