最小生成树概念:
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。 最小生成树可以用kruskal(克鲁斯卡尔)算法或prim(普里姆)算法求出。最小生成树其实是最小权重生成树的简称。
prim:
普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小。
prim算法求最小生成树的时候和边数无关,和顶点树有关,所以适合求解稠密网的最小生成树。
prim算法的步骤包括:
1. 将一个图分为两部分,一部分归为点集U,一部分归为点集V,U的初始集合为{V1},V的初始集合为{ALL-V1}。
2. 针对U开始找U中各节点的所有关联的边的权值最小的那个,然后将关联的节点Vi加入到U中,并且从V中删除(注意不能形成环)。
3. 递归执行步骤2,直到V中的集合为空。
4. U中所有节点构成的树就是最小生成树。
实现图解:
| 图例 | 说明 | 不可选 | 可选 | 已选(Vnew) |
|---|---|---|---|---|
|
|
此为原始的加权连通图。每条边一侧的数字代表其权值。 | - | - | - |
|
|
顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点,因此将A及对应边AD以高亮表示。 | C, G | A, B, E, F | D |
|
|
下一个顶点为距离D或A最近的顶点。B距D为9,距A为7,E为15,F为6。因此,F距D或A最近,因此将顶点F与相应边DF以高亮表示。 | C, G | B, E, F | A, D |
 |
算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。 | C | B, E, G | A, D, F |
|
|
在当前情况下,可以在C、E与G间进行选择。C距B为8,E距B为7,G距F为11。E最近,因此将顶点E与相应边BE高亮表示。 | 无 | C, E, G | A, D, F, B |
|
|
这里,可供选择的顶点只有C和G。C距E为5,G距E为9,故选取C,并与边EC一同高亮表示。 | 无 | C, G | A, D, F, B, E |
|
|
顶点G是唯一剩下的顶点,它距F为11,距E为9,E最近,故高亮表示G及相应边EG。 | 无 | G | A, D, F, B, E, C |
|
|
现在,所有顶点均已被选取,图中绿色部分即为连通图的最小生成树。在此例中,最小生成树的权值之和为39。 | 无 | 无 | A, D, F, B, E, C, G |
再来一张比较容易懂的图片:
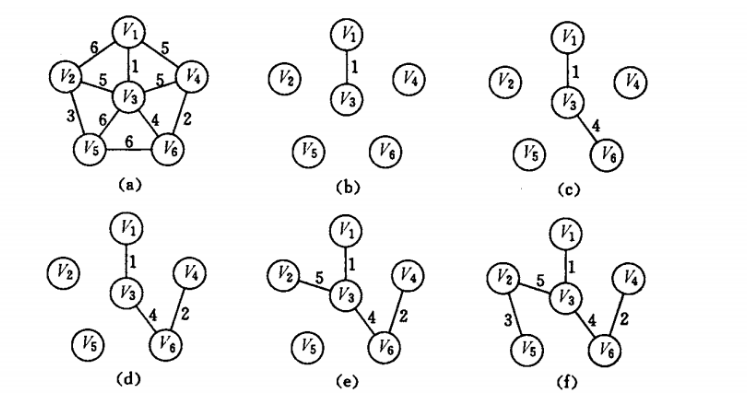
(a):一个无向图,记录了各点之间的权值关系
(b):在图中选择一个与{v1}连接最小的点v3
(c):选择一个与{v1,v3}连接最小的点v6
(d):选择一个与{v1,v3,v6}连接最小的点v4
(e):选择一个与{v1,v3,v6,v4}连接最小的点v2
(f):选择一个与{v1,v3,v6,v4,v2}连接最小的点v5
生成完毕。
Kruskal算法(并查集实现)
Kruskal是一种用来寻找最小生成树的算法,在剩下的所有未选取的边中,找最小边,如果和已选取的边构成回路,则放弃,选取次小边。
实现过程
1).记Graph中有v个顶点,e个边
2).新建图Graphnew,Graphnew中拥有原图中相同的e个顶点,但没有边
3).将原图Graph中所有e个边按权值从小到大排序
4).循环:从权值最小的边开始遍历每条边 直至图Graph中所有的节点都在同一个连通分量中 if 这条边连接的两个节点于图Graphnew中不在同一个连通分量中 添加这条边到图Graphnew中
图例描述:

首先第一步,我们有一张图Graph,有若干点和边

将所有的边的长度排序,用排序的结果作为我们选择边的依据。这里再次体现了贪心算法的思想。资源排序,对局部最优的资源进行选择,排序完成后,我们率先选择了边AD。这样我们的图就变成了下图

在剩下的变中寻找。我们找到了CE。这里边的权重也是5

依次类推我们找到了6,7,7,即DF,AB,BE。

下面继续选择, BC或者EF尽管现在长度为8的边是最小的未选择的边。但是现在他们已经连通了(对于BC可以通过CE,EB来连接,类似的EF可以通过EB,BA,AD,DF来接连)。所以不需要选择他们。类似的BD也已经连通了(这里上图的连通线用红色表示了)。最后就剩下EG和FG了。当然我们选择了EG。
代码:
prim;
#include<stdio.h> #include<string.h> #include <iostream> #include <bits/stdc++.h> #define IO ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); #define MAX 0x3f3f3f3f using namespace std; int logo[1010];//用来标记0和1 表示这个点是否被选择过 int map1[1010][1010];//邻接矩阵用来存储图的信息 int dis[1010];//记录任意一点到这个点的最近距离 int n;//点个数 int prim() { int i,j,now; int sum=0; /*初始化*/ for(i=1; i<=n; i++) { dis[i]=MAX; logo[i]=0; } /*选定1为起始点,初始化*/ for(i=1; i<=n; i++) { dis[i]=map1[1][i]; } dis[1]=0; logo[1]=1; /*循环找最小边,循环n-1次*/ for(i=1; i<n; i++) { now=MAX; int min1=MAX; for(j=1; j<=n; j++) { if(logo[j]==0&&dis[j]<min1) { now=j; min1=dis[j]; } } if(now==MAX) break;//防止不成图 logo[now]=1; sum+=min1; for(j=1; j<=n; j++)//添入新点后更新最小距离 { if(logo[j]==0&&dis[j]>map1[now][j]) dis[j]=map1[now][j]; } } if(i<n) printf("? "); else printf("%d ",sum); } int main() { while(scanf("%d",&n),n)//n是点数 { int m=n*(n-1)/2;//m是边数 memset(map1,0x3f3f3f3f,sizeof(map1));//map是邻接矩阵存储图的信息 for(int i=0; i<m; i++) { int a,b,c; scanf("%d%d%d",&a,&b,&c); if(c<map1[a][b])//防止重边 map1[a][b]=map1[b][a]=c; } prim(); } }
kruskal:
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; int n, m,sum; struct node { int start,end,power;//start为起始点,end为终止点,power为权值 } edge[5050]; int pre[5050]; int cmp(node a, node b) { return a.power<b.power;//按照权值排序 } int find(int x)//并查集找祖先 { if(x!=pre[x]) { pre[x]=find(pre[x]); } return pre[x]; } void merge(int x,int y,int n)//并查集合并函数,n是用来记录最短路中应该加入哪个点 { int fx=find(x); int fy=find(y); if(fx!=fy) { pre[fx]=fy; sum+=edge[n].power; } } int main() { while(~scanf("%d", &n), n)//n是点数 { sum=0; m=n*(n-1)/2;//m是边数,可以输入 int i; int start,end,power; for(i=1; i<=m; i++) { scanf("%d %d %d", &start, &end, &power); edge[i].start=start,edge[i].end=end,edge[i].power=power; } for(i=1; i<=m; i++) { pre[i]=i; }//并查集初始化 sort(edge+1, edge+m+1,cmp); for(i=1; i <= m; i++) { merge(edge[i].start,edge[i].end,i); } printf("%d ",sum); } return 0; }






