概念:
容量网络:设G(V,E),是一个有向网络,在V中指定了一个顶点,称为源点(记为Vs),以及另一个顶点,称为汇点(记为Vt);对于每一条弧<u,v>属于E,对应有一个权值c(u,v)>0,称为弧的容量.通常吧这样的有向网络G称为容量网络.
弧的流量:通过容量网络G中每条弧<u,v>,上的实际流量(简称流量),记为f(u,v);
网络流:所有弧上流量的集合f={f(u,v)},称为该容量网络的一个网络流.
可行流:在容量网络G中满足以下条件的网络流f,称为可行流.
a.弧流量限制条件: 0<=f(u,v)<=c(u,v);
b:平衡条件:即流入一个点的流量要等于流出这个点的流量,(源点和汇点除外).
若网络流上每条弧上的流量都为0,则该网络流称为零流.
伪流:如果一个网络流只满足弧流量限制条件,不满足平衡条件,则这种网络流为伪流,或称为容量可行流.(预流推进算法有用)
最大流:在容量网络中,满足弧流量限制条件,且满足平衡条件并且具有最大流量的可行流,称为网络最大流,简称最大流.
弧的类型:
a.饱和弧:即f(u,v)=c(u,v);
b.非饱和弧:即f(u,v)<c(u,v);
c.零流弧:即f(u,v)=0;
d.非零流弧:即f(u,v)>0.
链:在容量网络中,称顶点序列(u1,u2,u3,u4,..,un,v)为一条链要求相邻的两个顶点之间有一条弧.
设P是G中一条从Vs到Vt的链,约定从Vs指向Vt的方向为正方向.在链中并不要求所有的弧的方向都与链的方向相同.
a.前向弧:(方向与链的正方向一致的弧),其集合记为P+,
b.后向弧:(方向与链的正方向相反的弧),其集合记为P-.
增广路:
设f是一个容量网络G中的一个可行流,P是从Vs到Vt 的一条链,若P满足以下条件:
a.P中所有前向弧都是非饱和弧,
b.P中所有后向弧都是非零弧.
则称P为关于可行流f 的一条增广路.
沿这增广路改进可行流的操作称为增广.
残留容量:给定容量网络G(V,E),及可行流f,弧<u,v>上的残留容量记为cl(u,v)=c(u,v)-f(u,v).每条弧上的残留容量表示这条弧上可以增加的流量.因为从顶点u到顶点v的流量减少,等效与从顶点v到顶点u的流量增加,所以每条弧<u,v>上还有一个反方向的残留容量cl(v,u)=-f(u,v).
残留网络:设有容量网络G(V,E)及其上的网络流f,G关于f的残留网络记为G(V',E').其中G'的顶点集V'和G中顶点集G相同,V'=V.对于G中任何一条弧<u,v>,如果f(u,v)<c(u,v),那么在G'中有一条弧<u,v>属于E',其容量为c'(u,v)=c(u,v)-f(u,v),如果f(u,v)>0,则在G'中有一条弧<v,u>属于E',其容量为c'(v,u)=f(u,v).残留网络也称为剩余网络.
下面是所有最大流算法的精华部分:引入反向边
为什么要有反向边呢?

我们第一次找到了1-2-3-4这条增广路,这条路上的delta值显然是1。于是我们修改后得到了下面这个流。(图中的数字是容量)

这时候(1,2)和(3,4)边上的流量都等于容量了,我们再也找不到其他的增广路了,当前的流量是1。
但这个答案明显不是最大流,因为我们可以同时走1-2-4和1-3-4,这样可以得到流量为2的流。
那么我们刚刚的算法问题在哪里呢?问题就在于我们没有给程序一个”后悔”的机会,应该有一个不走(2-3-4)而改走(2-4)的机制。那么如何解决这个问题呢?回溯搜索吗?那么我们的效率就上升到指数级了。
而这个算法神奇的利用了一个叫做反向边的概念来解决这个问题。即每条边(I,j)都有一条反向边(j,i),反向边也同样有它的容量。
我们直接来看它是如何解决的:
在第一次找到增广路之后,在把路上每一段的容量减少delta的同时,也把每一段上的反方向的容量增加delta。即在Dec(c[x,y],delta)的同时,inc(c[y,x],delta)
我们来看刚才的例子,在找到1-2-3-4这条增广路之后,把容量修改成如下
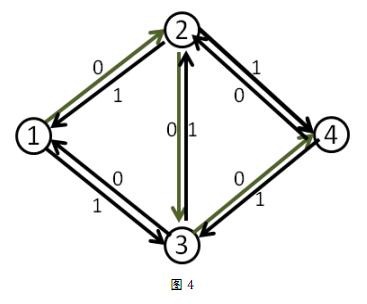
这时再找增广路的时候,就会找到1-3-2-4这条可增广量,即delta值为1的可增广路。将这条路增广之后,得到了最大流2。

那么,这么做为什么会是对的呢?我来通俗的解释一下吧。
事实上,当我们第二次的增广路走3-2这条反向边的时候,就相当于把2-3这条正向边已经是用了的流量给”退”了回去,不走2-3这条路,而改走从2点出发的其他的路也就是2-4。(有人问如果这里没有2-4怎么办,这时假如没有2-4这条路的话,最终这条增广路也不会存在,因为他根本不能走到汇点)同时本来在3-4上的流量由1-3-4这条路来”接管”。而最终2-3这条路正向流量1,反向流量1,等于没有流量。
EK算法
EK算法的核心
反复寻找源点s到汇点t之间的增广路径,若有,找出增广路径上每一段[容量-流量]的最小值delta,若无,则结束。
在寻找增广路径时,可以用BFS来找,并且更新残留网络的值(涉及到反向边)。
而找到delta后,则使最大流值加上delta,更新为当前的最大流值。
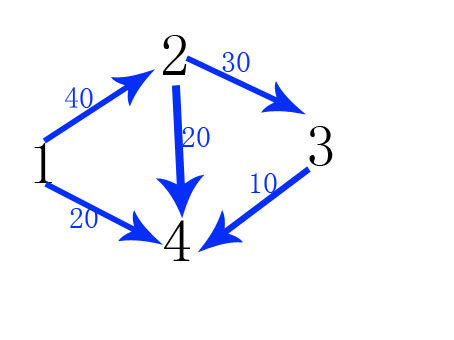
对于BFS找增广路:
1. flow[1]=INF,pre[1]=0;
源点1进队列,开始找增广路,capacity[1][2]=40>0,则flow[2]=min(flow[1],40)=40;
capacity[1][4]=20>0,则flow[4]=min(flow[1],20)=20;
capacity[2][3]=30>0,则flow[3]=min(folw[2]=40,30)=30;
capacity[2][4]=30,但是pre[4]=1(已经在capacity[1][4]这遍历过4号点了)
capacity[3][4].....
当index=4(汇点),结束增广路的寻找
传递回increasement(该路径的流),利用前驱pre寻找路径
路径也自然变成了这样:

2.flow[1]=INF,pre[1]=0;
源点1进队列,开始找增广路,capacity[1][2]=40>0,则flow[2]=min(flow[1],40)=40;
capacity[1][4]=0!>0,跳过
capacity[2][3]=30>0,则flow[3]=min(folw[2]=40,30)=30;
capacity[2][4]=30,pre[4]=2,则flow[2][4]=min(flow[2]=40,20)=20;
capacity[3][4].....
当index=4(汇点),结束增广路的寻找
传递回increasement(该路径的流),利用前驱pre寻找路径
图也被改成

接下来同理
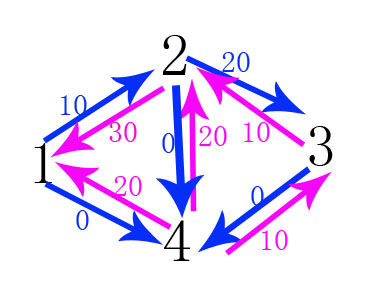
这就是最终完成的图,最终sumflow=20+20+10=50(这个就是最大流的值)
EK模板:
problem:hdu 1532
#include <iostream> #include <stdio.h> #include <cmath> #include <ios> #include <string.h> #include <queue> #include <algorithm> #include <iomanip> #define MAX 0x3f3f3f3f #define IO ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); using namespace std; const int N = 205; int r[N][N],pre[N]; bool vis[N]; int n,m;//n边,m点 bool BFS(int s,int t){ queue<int > que; memset(pre,-1,sizeof(pre)); memset(vis,0,sizeof(vis)); pre[s] = s; vis[s] = 1; que.push(s); while(!que.empty()){ int p = que.front(); que.pop(); for(int i = 1;i <=m; i++){ if(r[p][i]>0 && !vis[i]){ pre[i] = p; vis[i] = 1; if(i == t) return 1; que.push(i); } } } return 0; } int EK(int s,int t){ int maxflow = 0,d; while(BFS(s,t)) { d = MAX; for(int i = t; i != s; i = pre[i]) //寻找增广路中最小的残量 d = min(d,r[pre[i]][i]); for(int i = t; i != s; i = pre[i]){ r[pre[i]][i] -= d; r[i][pre[i]] += d; } maxflow +=d; } return maxflow; } int main() { IO while(cin>>n>>m){ memset(r,0,sizeof(r)); int s,e,c; for(int i = 0; i < n; i++){ cin>>s>>e>>c; r[s][e] += c; } cout<<EK(1,m)<<endl; } return 0; }