一:二叉树的概念:
二叉树指的是每个节点最多只能有两个子树的有序树。通常左边的子树被称为“左子树”,右边的子树被称为“右子树”。由此可见,二叉树仍然是树,只是一种特殊的树。
二叉树的每个节点最多只有两棵子树(不存在大于2的节点)。二叉树有左、右之分,不能颠倒。
树和二叉树的两个重要区别如下:
1.树中节点的最大度数没有限制,而二叉树节点的最大度数为2,也就是说,二叉树的节点最大度数为2。
2.无序树的节点无左右之分,而二叉树的节点有左右之分,也就是说二叉树是有序树。
满二叉树:
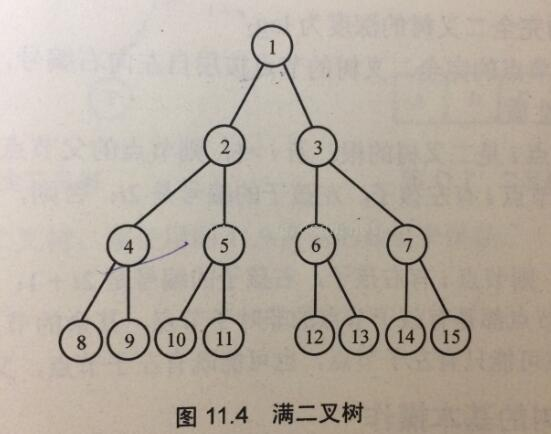
一棵深度为K的二叉树,如果它包含了2^K - 1个节点,就把这棵二叉树称为满二叉树。满二叉树的特点是,每一层上的节点数都是最大节点数,即各层节点数分别为1,2,4,8,16,32,……,2^(K-1) 。
完全二叉树:
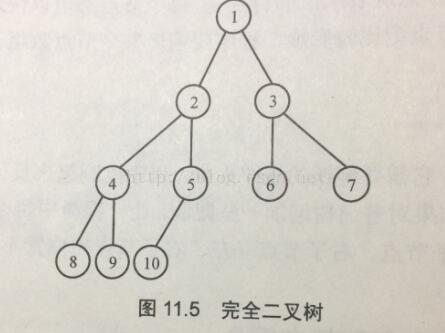
如果一棵二叉树除最后一层外,其余所有的节点都是满的,并且最后一层或者是满的,或者仅在右边缺少若干连续的节点,则此二叉树就是完全二叉树。
区别:满二叉树是一种特殊的完全二叉树。当完全二叉树最后一层的所有节点都是满的情况下,这棵完全二叉树就变成了满二叉树。
二:实现二叉树的基本操作:
首先定义我们的节点类:
1 package mytree; 2 3 public class Node { 4 int value;//值域 5 Node left;//左子节点 6 Node right;//右子节点 7 public Node(int value) { 8 this.value=value; 9 } 10 @Override 11 public String toString() { 12 return String.valueOf(value); 13 } 14 15 public void display(){ 16 System.out.print(this.value+" "); 17 } 18 19 }
定义我们的方法类:
1 public class BinaryTree { 2 private Node root = null; 3 4 public BinaryTree(int value) { 5 root = new Node(value); 6 root.left = null; 7 root.right = null; 8 } 9 }
1.实现添加节点:
第一种:
1 public String insert(int value) { // 插入 2 String error = null;//错误 3 Node now = new Node(value);//创建要插入的节点 4 Node curr = root;//获取到根节点 5 if (curr == null) {//如果根节点为空 6 curr = now;//就把要插入的节点作为根节点 7 } else { 8 while (true) { 9 Node parent = null;//先创建一个临时存放节点 10 if (curr.value > value) {//如过当前节点>要插入的节点,就把节点插入到左子节点 11 parent = curr;//把主节点赋值给他 12 curr = curr.left;//获取到左子节点 13 if (curr == null) {//如果左子节点为空的话 14 parent.left = now;//插入 15 break; 16 } 17 } else if (curr.value < value) { 18 parent = curr; 19 curr = curr.right; 20 if (curr == null) { 21 parent.right = now; 22 break; 23 } 24 } else { 25 error = "树里面有了相同的值:"; 26 } 27 } 28 } 29 return error; 30 }
第二种递归添加:
1 /* 2 * 插入递归调用实现 3 * 4 * */ 5 public Node insert2(Node node, int data) { 6 if (node == null) { 7 node = new Node(data); 8 } else { 9 if (data <= node.value) { 10 node.left = insert2(node.left, data); 11 } else { 12 node.right = insert2(node.right, data); 13 } 14 } 15 return (node); 16 } 17
2.定义一个直接返回整个二叉树的方法:
1 public Node getrootNode(){//返回整个二叉树 2 return root; 3 }
3.定义一个遍历节点的方法(中序遍历):
1 /** 2 * //中序遍历(递归): 3 * 1、调用自身来遍历节点的左子树 4 * 2、去取得当前节点 5 * 3、调用自身来遍历节点的右子树 6 */ 7 public void inOrderTraverse(Node node) { 8 if (node == null) 9 return ; 10 inOrderTraverse(node.left); 11 node.display(); 12 inOrderTraverse(node.right); 13 } 14
4.我们创建一个测试类看看我们的方法是不是写的都是正确的:
1 package mytree; 2 3 public class Test { 4 5 public static void main(String[] args) { 6 // TODO Auto-generated method stub 7 BinaryTree b=new BinaryTree(12); 8 b.insert(10);//普通插入方法 9 Node no=b.getrootNode();//获取到二叉树对象 10 b.insert2(no, 20);//通过递归插入 11 no=b.getrootNode(); 12 b.inOrderTraverse(no);//中序遍历 13 } 14 }
运行为:

看来写的添加节点与遍历节点都是可以的;
5.前序遍历:
1 /*前序遍历 2 * 访问节点 3 * 访问自身来遍历左子树 4 * 访问自身来遍历右子树 5 * */ 6 public void PreOrderTraverse(Node node) { 7 if (node == null) 8 return; 9 inOrderTraverse(node.left); 10 node.display(); 11 inOrderTraverse(node.right); 12 }
6.后序遍历:
1 /*后序遍历 2 * 3 * 访问自身来遍历左子树 4 * 访问自身来遍历右子树 5 * 访问节点 6 * */ 7 public void nexOrderTraverse(Node node) { 8 if (node == null) 9 return; 10 inOrderTraverse(node.left); 11 inOrderTraverse(node.right); 12 node.display(); 13 }
7.得到最小值:(其实也就是一直遍历左子树直到空)
1 public int getMinValue() { 2 Node current = root; 3 while (true) { 4 if (current.left== null) 5 return current.value; 6 7 current = current.left; 8 } 9 }
8.得到最大值:(其实也就是一直遍历右子树直到空)
1 2 public int getMaxValue() { 3 Node current = root; 4 while (true) { 5 if (current.right== null) 6 return current.value; 7 8 current = current.right; 9 } 10 }
临时有事,查找删除再整理;