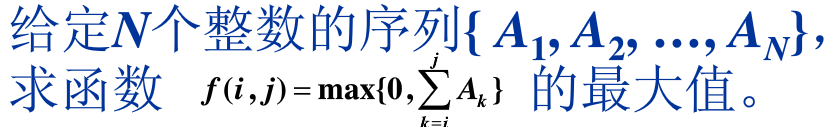
方法1:暴力计算法
i 表示子列开始索引
j 表示子列结束索引
k(i<k<j) 辅助计算 i~j之间子列和
public int method1(int[] arr) { int maxSum = 0; for (int i = 0; i < arr.length; i++) { for (int j = i; j < arr.length; j++) { int tempMax = 0; for (int k = i; k <= j; k++) { tempMax += arr[k]; } if (tempMax > maxSum) { maxSum = tempMax; } } } return maxSum; }
三层for循环,时间复杂度 T(N) = n^3
方法2:暴力破解优化
因为方法一每次都是从 i 加到 j ,而 j 每次只往后扫描变化一个,所以直接将 k 循环省略在 j 循环中计算
public int method2(int[] arr) { int maxSum = 0; for (int i = 0; i < arr.length; i++) { int tempSum = 0; for (int j = i; j <= arr.length; j++) { tempSum += arr[j];
if (tempSum > maxSum) {
maxSum = tempSum;
}
}
}
return maxSum;
}
两层for循环,T(N) = n^2
方法3:分治策略,将问题划分为更小的问题,解决后再返回来求最优解
/** * 为了与方法1和2有同样的调用接口 * @param arr * @return */ public int method3(int[] arr) { return divideAndConquer(arr, 0, arr.length - 1); } /** * 将数组划分为两部分,先计算左半部分最大子列和,再计算又半部分最大子列和,再从分界线向左向右分别扫描获取最大子列和取得跨界最大子列和 * * @param arr * @param left * @param right * @return */ private int divideAndConquer(int[] arr, int left, int right) { /** * 如果索引相等,表示已经划分该部分为最小问题,元素个数为1 * 若该元素大于0,则对计算下一步运算有帮助,返回原值 * 若该元素小于0,则无论向左向右加都会减小相邻子列的和,所以舍弃该元素,返回0 */ if (left == right) { if (arr[left] > 0) { return arr[left]; } else { return 0; } } /* 下面是"分"的过程 */ int mid = (left + right) / 2; /* 求最大左子列和 */ int maxLeftSum = divideAndConquer(arr, left, mid); /* 求最大右子列和 */ int maxRightSum = divideAndConquer(arr, mid + 1, right); /* 求跨界最大子列和 */ int maxLeftBorderSum = 0; int maxRightBorderSum = 0; int leftBorderSum = 0; int rightBorderSum = 0; /* 从中线向左扫描 */ for (int i = mid; i >= left; i--) { leftBorderSum += arr[i]; if (leftBorderSum > maxLeftBorderSum) { maxLeftBorderSum = leftBorderSum; } } /* 从中线向右扫描 */ for (int i = mid + 1; i < right; i++) { rightBorderSum += arr[i]; if (rightBorderSum > maxRightBorderSum) { maxRightBorderSum = rightBorderSum; } } /* 返回该分段中最左,最右,跨界三者中最大数作为该分段最大子列和 */ return max3(maxLeftSum, maxRightSum, maxLeftBorderSum + maxRightBorderSum); } /** * 求三整数最大值 * 计算顺序 * a > b ? (a > c ? a : c) : (b > c ? b : c) * @param a * @param b * @param c * @return */ private int max3(int a, int b, int c) { return a > b ? a > c ? a : c : b > c ? b : c; }
T(N) = T(N/2) + cN
求解得时间复杂度 T(N) = nlogn
方法4:在线处理方法,扫描一个元素解决当前阶段最大子列和
/** * 在线处理 * * @param arr */ public int method4(int[] arr) { int maxSeqSum = 0; int tempMax = 0; for (int i = 0; i < arr.length; i++) { tempMax += arr[i]; // 向右累加 if (tempMax > maxSeqSum) { maxSeqSum = tempMax; // 发现更大的和则更新当前结果 } else if (tempMax < 0) { // 如果当前子列和为负 tempMax = 0; // 则不可能使后面的部分和增大,抛弃之 } } return maxSeqSum; }
每个元素最少都要扫描一遍,时间复杂度T(N) = n
运行代码
public class SearchMaxQueueSum { public static void main(String[] args) { int[] arr = new int[]{-1, 3, -2, 4, -6, 1, 6, -1}; SearchMaxQueueSum searchMaxQueueSum = new SearchMaxQueueSum(); int seqSumFromMethod1 = searchMaxQueueSum.method1(arr); int seqSumFromMethod2 = searchMaxQueueSum.method3(arr); int seqSumFromMethod3 = searchMaxQueueSum.method3(arr); int seqSumFromMethod4 = searchMaxQueueSum.method4(arr); System.out.println("method1: "+seqSumFromMethod1); System.out.println("method2: "+seqSumFromMethod2); System.out.println("method3: "+seqSumFromMethod3); System.out.println("method4: "+seqSumFromMethod4); } public int method1(int[] arr) { int maxSum = 0; for (int i = 0; i < arr.length; i++) { for (int j = i; j < arr.length; j++) { int tempMax = 0; for (int k = i; k <= j; k++) { tempMax += arr[k]; } if (tempMax > maxSum) { maxSum = tempMax; } } } return maxSum; } public int method2(int[] arr) { int maxSum = 0; for (int i = 0; i < arr.length; i++) { int tempSum = 0; for (int j = i; j <= arr.length; j++) { tempSum += arr[j]; if (tempSum > maxSum) { maxSum = tempSum; } } } return maxSum; } /** * 为了与方法1和2有同样的调用接口 * @param arr * @return */ public int method3(int[] arr) { return divideAndConquer(arr, 0, arr.length - 1); } /** * 将数组划分为两部分,先计算左半部分最大子列和,再计算又半部分最大子列和,再从分界线向左向右分别扫描获取最大子列和取得跨界最大子列和 * * @param arr * @param left * @param right * @return */ private int divideAndConquer(int[] arr, int left, int right) { /** * 如果索引相等,表示已经划分该部分为最小问题,元素个数为1 * 若该元素大于0,则对计算下一步运算有帮助,返回原值 * 若该元素小于0,则无论向左向右加都会减小相邻子列的和,所以舍弃该元素,返回0 */ if (left == right) { if (arr[left] > 0) { return arr[left]; } else { return 0; } } /* 下面是"分"的过程 */ int mid = (left + right) / 2; /* 求最大左子列和 */ int maxLeftSum = divideAndConquer(arr, left, mid); /* 求最大右子列和 */ int maxRightSum = divideAndConquer(arr, mid + 1, right); /* 求跨界最大子列和 */ int maxLeftBorderSum = 0; int maxRightBorderSum = 0; int leftBorderSum = 0; int rightBorderSum = 0; /* 从中线向左扫描 */ for (int i = mid; i >= left; i--) { leftBorderSum += arr[i]; if (leftBorderSum > maxLeftBorderSum) { maxLeftBorderSum = leftBorderSum; } } /* 从中线向右扫描 */ for (int i = mid + 1; i < right; i++) { rightBorderSum += arr[i]; if (rightBorderSum > maxRightBorderSum) { maxRightBorderSum = rightBorderSum; } } /* 返回该分段中最左,最右,跨界三者中最大数作为该分段最大子列和 */ return max3(maxLeftSum, maxRightSum, maxLeftBorderSum + maxRightBorderSum); } /** * 求三整数最大值 * 计算顺序 * a > b ? (a > c ? a : c) : (b > c ? b : c) * @param a * @param b * @param c * @return */ private int max3(int a, int b, int c) { return a > b ? a > c ? a : c : b > c ? b : c; } /** * 在线处理 * * @param arr */ public int method4(int[] arr) { int maxSeqSum = 0; int tempMax = 0; for (int i = 0; i < arr.length; i++) { tempMax += arr[i]; // 向右累加 if (tempMax > maxSeqSum) { maxSeqSum = tempMax; // 发现更大的和则更新当前结果 } else if (tempMax < 0) { // 如果当前子列和为负 tempMax = 0; // 则不可能使后面的部分和增大,抛弃之 } } return maxSeqSum; } }
运行结果
