(一)前置技能
1.网络流最大流((dinic), (Edmonds-Karp)都可以)
2.建图(邻接链表,反向边^1的小技巧)
达成了 1 阅读本文将很轻松,达成了 2 阅读代码将很轻松
(二)题目描述
简单地阐述一下题意:
有 (n) 个 (A) 类节点,(p) 个 (B) 类节点, (q) 个 (C) 类节点。每个 (A) 与一个 (B) 和一个 (C) 构成一组匹配(每个(A)只能与给定的(B)、(C)匹配,且每个(B)、(C)只能匹配一个(A)),求最大匹配数。
(三)解题思路
简化之后的题意很像二分图匹配,二分图匹配是一个点匹配一个点,而本题是一个点匹配两个点。
起先,我是想将 (A) 类节点放在左边,(B) 类节点放中, (C) 类最右。顺着题意用(A)匹配(B)和(C)的,然后发现,这样子根本无法建图!!!
因为题目只给出了(A)——(B), (A)——(C)的关系,根本不知道(B)与(C)的关系。倘若按上面方式建图的话,(B)和(C)就会成为并列的节点。很明显这是不符合题意的。
那该如何建图呢?
既然已经知道(B)与(A)的关系、(A)与(C)的关系,不妨直接将(A)放在中间,(RT):
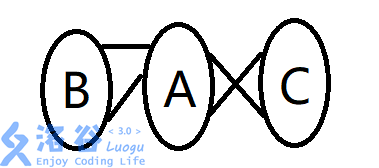
如此,得到了一张三分图,再求此图的最大匹配即可。
方法一:匈牙利算法
从(A)出发直接向(B)和(C)跑两次二分图匹配即可。这里不作详细解释。
方法二:网络流最大流
按照网络流的正常操作,建立一个超级源点(S),连接所有(B),流量为1; 建立一个超级汇点(T), 使所有(C)都连向(T),流量为1。再根据题目所给的关系连接(B)——(A)、(A)——(C)。
可能很多同学看到这里都会想:会了会了,然后再跑网络流最大流嘛。
不要以为这样就可以了。这可是三分图匹配呀,哪有那么简单!
看下面这幅图你就会知道哪里错了。
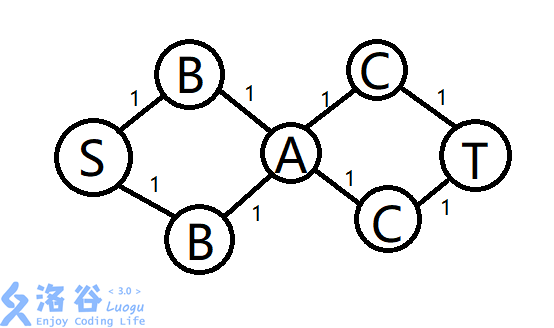
如果光是按上述方法建图的话,那么图就会变成上面那样,最大流跑出来是2。
然而我们知道,最大流不能是2,因为任意(B)、(C)只能匹配一个(A)。
如何解决上述问题呢?
很简单,只需要将(A)拆分为两个点即可,(RT)。
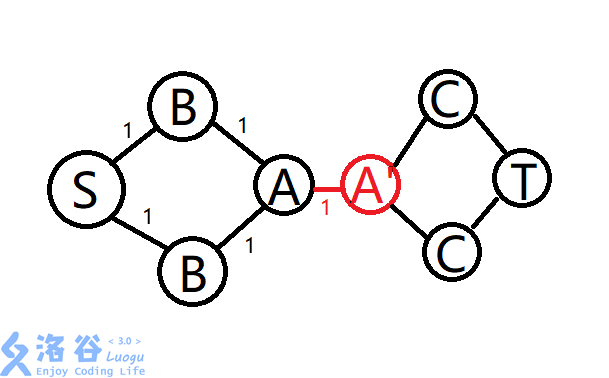
连接(A)和(A'),流量为1。
即可避免多个(B)、(C)重复匹配一个(A)的情况了。
终于可以上代码了:(我太菜了,不会(dinic),所以只能写(E-K)了)
#include<bits/stdc++.h>
using namespace std;
const int maxn = 105, maxm = 10000005, INF = 2147483647;
int head[maxn<<2], ver[maxm], edge[maxm], Next[maxm], tot;
void add(int x,int y,int z)
{
ver[++tot] = y, edge[tot] = z, Next[tot] = head[x], head[x] = tot;
ver[++tot] = x, edge[tot] = 0, Next[tot] = head[y], head[y] = tot;
}
int n, p, q;
//A:1~n, B:n+1~n+p, C:n+p+1~n+p+q, A':n+p+q+1~n+p+q+n
int s, t, maxflow, incf[maxn<<2], pre[maxn<<2];bool vis[maxn<<2];
bool bfs()
{
for(int i=1; i<=n+p+q+n+2; i++) vis[i] = false;
queue<int> Q;
Q.push(s), vis[s] = true, incf[s] = INF;
while(!Q.empty())
{
int x = Q.front(); Q.pop();
for(int i=head[x]; i; i=Next[i])
if(edge[i])
{
int y = ver[i];
if(vis[y]) continue;
incf[y] = min(incf[x], edge[i]), pre[y] = i;
vis[y] = true;
if(y == t) return true;
Q.push(y);
}
}
return false;
}
void update()
{
int x = t;
while(x!=s)
{
int i = pre[x];
edge[i] -= incf[t];
edge[i^1] += incf[t];
x = ver[i^1];
}
maxflow+=incf[t];
}
int main()
{
tot = 1;
scanf("%d%d%d",&n,&p,&q);
s = n+p+q+n+1, t = n+p+q+n+2;
for(int i=1; i<=n; i++)
for(int j=1; j<=p; j++)
{
bool x;
scanf("%d",&x);
if(x) add(j+n, i, 1);
}
for(int i=1; i<=n; i++)
for(int j=1; j<=q; j++)
{
bool x;
scanf("%d",&x);
if(x) add(i+n+p+q, j+n+p, 1);
}
for(int i=1; i<=p; i++) add(s, i+n, 1);
for(int i=1; i<=q; i++) add(i+n+p, t, 1);
for(int i=1; i<=n; i++) add(i, i+n+p+q, 1);
while(bfs()) update();
printf("%d", maxflow);
return 0;
}
(四)总结
这道题是一道非常好的题目,它的建图方式很新颖。
网络流的题目考的无非就是建图,只要把图建好了,还有什么题搞不掂?