01分数规划问题

数学描述

给定(n)个二元组((value_i, cost_i))。(value_i)是选择此二元组获得的价值（非负）, (cost_i)是选择此二元组付出的代价（非负），设(x _i) (( x_i ∈ { 0 , 1 } ))代表第(i)个二元组的选与不选，最大(小)化下式

(maximize(or minimize) r = frac{sum{(value_i*x_i)}}{sum{(cost_i * x_i)}})

问题引入

为了便于理解该问题解法的推导过程，通过以下问题的解决过程引出基本01分数规划问题的解法
问题描述
给定一张(L)个点、(P)条边的有向图，每个点都有一个权值(f[i])，每条边都有一个权值(t[i])。
求图中的一个环，使“环上各点的权值之和”除以“环上各边的权值之和”最大。
输出这个最大值。
[注]: 数据保证至少存在一个环

输入格式
第一行包含两个整数(L) 和 (P)。
接下来(L)行每行一个整数，表示(f[i])。
再接下来 (P) 行，每行三个整数 (a，b，t[i])，表示点 (a) 和 (b) 之间存在一条边，边的权值为 (t[i])。

输出格式
输出一个数表示结果，保留两位小数。

数据范围
(2≤L≤1000),
(2≤P≤5000),
(1≤f[i],t[i]≤1000)

输入样例

5 7
30
10
10
5
10
1 2 3
2 3 2
3 4 5
3 5 2
4 5 5
5 1 3
5 2 2

输出样例

6.00

解决思路

此题型的解决方法为二分+spfa判负环
本题是求最值的问题，所以二分不难想到，然后还需要判断是否可以采用二分

1. 使用二分的首要条件是二分对象的取值是可知的

• 条件1满足，答案区间为((0, 1000])

2. 满足条件1之后，给定一个mid，假设具有某种方法来判定一个该值是否符合条件，考虑在得知此值合法性的前提下，是否可以将原取值范围缩减

• 条件2满足，给定一个mid值，假设(frac{sum{f[i]}}{sum{t[i]}} > mid)，那么答案处在mid的右半区间，反之处在左半区间

3. 如果满足了条件2，那么考虑是否具有某种方法来判定mid的合法性，如果不能判断那么前面的假设就不成立，二分法不可取，反之可取

• 需要判断(frac{sum{f[i]}}{sum{t[i]}})与(mid)的大小关系，那么就假设(frac{sum{f[i]}}{sum{t[i]}} > mid)，推导后可得(mid * sum{t[i]} - sum{f[i]} < 0)。即对于一个边权为(mid*t-f)的图，判断是否存在一个负环(注意后面这里是t和f，代表一个点权和边权，而非点权和，边权和)来判断mid的合法性，条件3成立
  

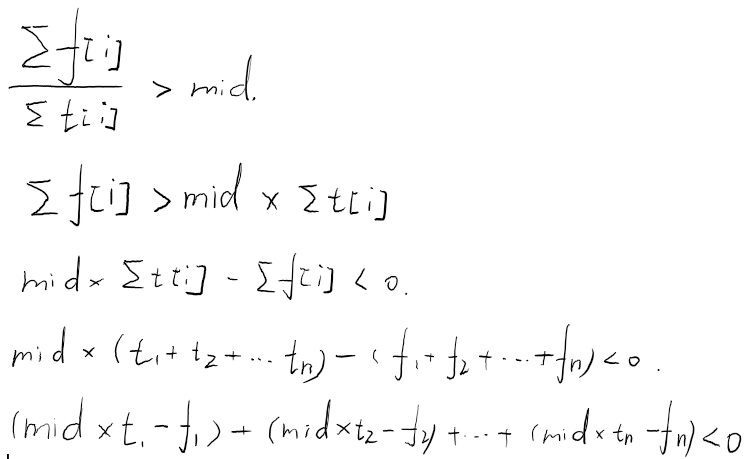
代码实现

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 1010, M = 5010;

int n, m;
int f[N];
bool st[N];
int cnt[N];
double dis[N];
int h[N], e[M], ne[M], w[M], idx;

void add(int a, int b, int t)
{
    w[idx] = t;
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++;
}
// 有负环返回true，否则返回false
bool spfa(double x)
{
    queue<int> q;
    for (int i = 1; i <= n; ++ i)
    {
        cnt[i] = 0;
        dis[i] = 0.0;
        q.push(i);
        st[i] = true;
    }

    while (q.size())
    {
        int t = q.front(); q.pop();
        st[t] = false;

        for (int i = h[t]; ~i; i = ne[i])
        {
            int p = e[i];
            if (dis[p] > dis[t] + x * w[i] - f[t])
            {
                dis[p] = dis[t] + x * w[i] - f[t];
                cnt[p] = cnt[t] + 1;

                if (cnt[p] >= n) return true;
                if (!st[p])
                {
                    q.push(p);
                    st[p] = true;
                }
            }
        }
    }

    return false;
}
int main()
{
   
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i)
        cin >> f[i];

    memset(h, -1, sizeof h);    
    for (int i = 0; i < m; ++ i)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    
    double l = 0.0, r = 1000.0;
    const double eps = 1e-6;
    while (r - l > eps)
    {
        double mid = (l + r) / 2.0;
        if (spfa(mid)) l = mid;
        else r = mid; // 浮点数不需要加减1
    }

    printf("%.2lf
", l);

    return 0;
}