第1章-概论
-
冯·诺依曼提出的新型计算机的五大结构: 运算器,控制器,存储器,输入设备和输出设备
-
计算机主要性能指标
- 基本字长: 处理器中参加一次定点运算的操作位的位数(计算机中的算术运算分为定点运算和浮点运算)
- 外频: 主板上的振荡器输出的时钟频率,也是计算机一切硬件部件工作所依据的基准时钟信号
- CPU的主频: CPU内核的工作频率,(CPU主频 = 外频 * 倍频系数)。
- IPS: 平均每秒执行的指令数(Instructions Per Second)
- CPI: 平均每条指令的时钟周期数(Clock cycles Per Instructions)
第2章-数据的表示、运算和校验
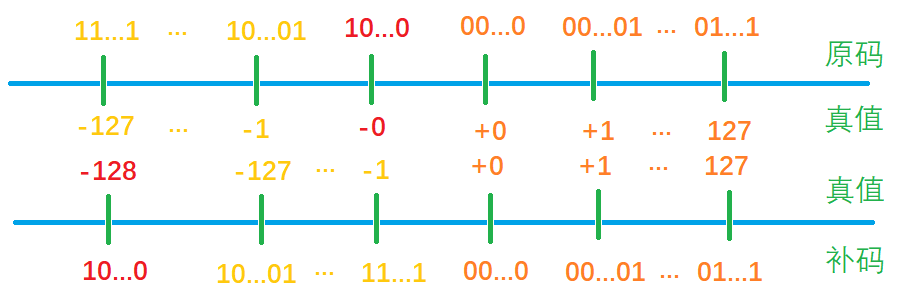
8位有符号数原码和补码的范围区别:
- 原码: (-127 sim 127(11111111 sim 01111111))
- 反码: (-128 sim 127(10000000 sim 01111111))
当数据(>+0)时,由于原码和补码是相同的,所以从(0)到(127)是一一对应的
当数据(<+0)时,从(-127)到(-1)是一一对应的
关键点在于原码中存在一个(-0),对应二进制为(10000000),在转化为补码时会出现溢出的问题,所以就将(10000000)作为补码中的(-128)
定点数和浮点数
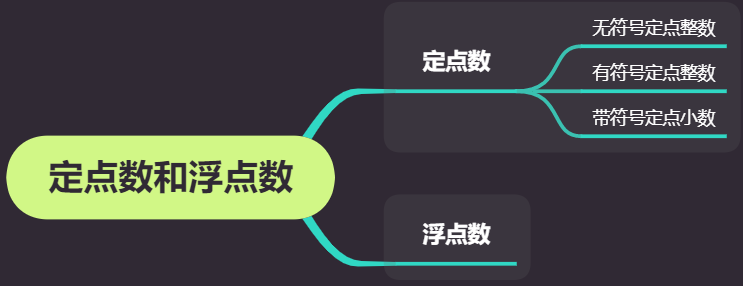
定点数
- (n)位无符号定点整数范围: (0 sim 2^n - 1)
- (n)位有符号定点整数范围:
原码:(-(2^{n-1}-1) sim 2^{n-1}-1)
补码:(-2^{n-1} sim 2^{n-1}-1) - 有符号定点小数:最高位是符号位,小数点后为有效位(x.xxxxx)
同有符号定点整数一样,原码存在(1.00000000)的(-0),但在补码中其对应着(-1)
浮点数
-
表示形态: (N = pm R^E imes M)
(N)为真值,(R^E)为比例因子,(M)为尾数

-
规格化
规格化要求: (frac{1}{2} leq |M| < 1)
对于正数,无论原码还是补码,规格化特征为(M_1 = 1)
对于负数,原码规格化特征为(M_1 = 1),补码规格化特征为(M_1 = 0)
原因在于判断(M)的值时,负数的补码需要先转化为原码,补码的(M_1 = 0)才能保证$ |M| geq frac{1}{2}$注:规格化时有两个特殊的数值(-1)和(-frac{1}{2})
(-1)在原码表示中不符合规格化要求(原码表示不会出现(-1)),但补码中符合(因为(-1)补码1.0的特殊性)
(-frac{1}{2})在原码表示中符合规格化要求,但补码中不符合(原码和补码都是1.1)
定点数的四则运算
加减法
计算规则
需要说明的是:
((-y)_补)可以在y的原码基础上将符号位取反获得-y的原码,之后除符号位取反加1获得补码
也可以直接对y求变补,即对包含符号位的所有位取反再加1。两种方法本质上是一样的
符号位同样参与运算,当符号位产生进位时,丢弃掉最高位的进位
溢出判断
同号相加和异号相减会使得结果的绝对值增大从而可能产生溢出
-
判断方法1:
因为即使是减法运算,最终我们也是转化为了加法运算。设转化为加法运算后的数据为(A,B),对应的符号位依次是(S_a,S_b),运算后结果的符号位是(S_f)。则(v = overline{s_a} overline{s_b}s_f + s_as_b overline{s_f})。(v=1)变送发生了溢出,(v=0)表示未发生溢出。原理是当(s_a = s_b = 0, s_f = 1)(两正数相加,结果为负数)或(s_a = s_b = 1, s_f = 0)(两负数相加,结果为正数)时说明发生了溢出
-
判断方法2:
设(C)为最高有效数位(符号位低一位)产生的仅为,(C_f)为符号位产生的进位。(V = C oplus C_f)
-
判断方法3:
采用双符号位,00-结果为正,无溢出;11-结果为负,无溢出;01-结果正溢;10-结果负溢
设第一符号位和第二符号位依次位(S_{f1}, S_{f2}),(V = S_{f1} oplus S_{f2})
乘法
原码一位乘
取两操作数的绝对值进行相乘,具体过程见下图。

补码一位乘
原码两位乘
除法
原码不恢复余数
补码不恢复余数