计算不定方程的等式方程非负整数解的组数
问题描述
对于不定方程(a_1 + a_2 + a_3 + ... + a_k = g),求解该不定方程正整数解的组数
eg: (k = 3, g = 4)时,(①1 + 1 + 2 = 4 ②1 + 2 + 1 = 4 ③2 + 1 + 1 = 4),所以此时是三组解
问题分析
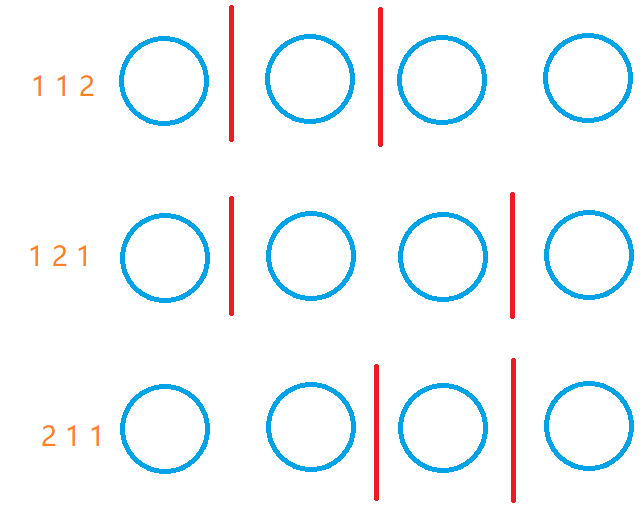
问题可等效为求解将(g)个小球分成(k)组的方案数
解决方法为隔板法。(g)个小球共(g-1)个间隔,(k-1)个隔板可以分为(k)个部分,在(g-1)个间隔中放置(k-1)个隔板的方案数即为答案
隔板法能够运用的前提条件为保证(a_i)为非负整数,这样使用隔板划分出的数据才是合法的。假设(a_i)可能为负数或0,使用隔板是无法得到对应数据的
代码实现
仅需要实现组合数的计算,具体内容见组合数的代码实现
例题
计算不定方程的不等式方程非负整数解的组数
问题描述
(y_1 + y_2 + y_3 + ... + y_k leq g)
(y_i geq 1)
求符合条件的(y_i)的解的组数
问题分析
对于等式(y_1 + y_2 + y_3 + ... + y_k = g),求解方法可以采用隔板法,这是在上面讨论过的
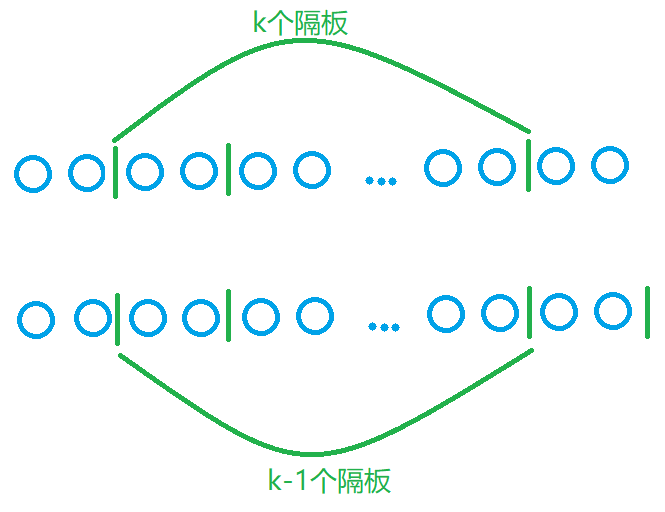
假设我们目前仅考虑(=)的情况,只需在(g-1)个间隔中放置(k-1)个隔板,从而构成k个数
接着考虑(<)的情况,此时形成的k个数需要小于g,即g个球中有未进入分组的,在(g-1)个间隔中放置(k)个隔板,这样构成的(k+1)个分组中最后一组就相当于未进入分组的,前k个数的和就(<g)了
综合考虑以上两种情况,最终策略为在(g-1)个间隔加上最后的位置中放置(k)个隔板。当隔板全部处于中间(g-1)个位置时,对应的是(<)的情况;当最后一个隔板处于最后的位置时,中间(g-1)个间隔中还是(k-1)个隔板,对应的是(=)的情况。
代码实现
同样仅需要实现组合数的计算,,具体内容见组合数的代码实现