合并果子

问题描述

在一个果园里，达达已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。
达达决定把所有的果子合成一堆。
每一次合并，达达可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。
可以看出，所有的果子经过n-1次合并之后，就只剩下一堆了。
达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家，所以达达在合并果子时要尽可能地节省体力。
假定每个果子重量都为1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使达达耗费的体力最少，并输出这个最小的体力耗费值。
例如有3种果子，数目依次为1，2，9。
可以先将1、2堆合并，新堆数目为3，耗费体力为3。
接着，将新堆与原先的第三堆合并，又得到新的堆，数目为12，耗费体力为12。
所以达达总共耗费体力=3+12=15。
可以证明15为最小的体力耗费值。

问题分析

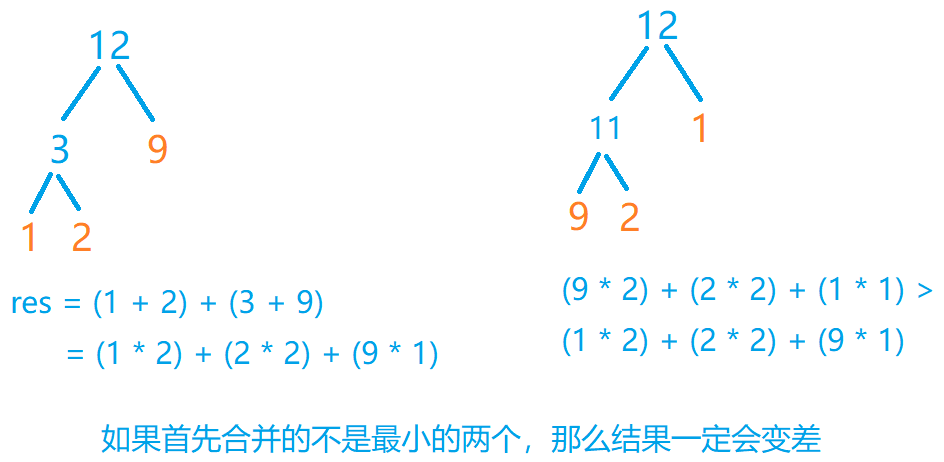
先合并最小的两个点一定是最优策略，原因在于根据哈夫曼树的结构，如果我们首先合并的是不是两个最小的点，那么我们一定可以换为首先合并两个最小的点，能够保证对后续的合并操作没有影响且保证换后的结果优于换前的结果(原因见下图)

代码实现

#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

int n;
priority_queue<int, vector<int>, greater<int>> heap;

int main()
{
    cin >> n;
    while (n --)
    {
        int x;
        cin >> x;
        heap.push(x);
    }
    
    int res = 0;
    while (heap.size() > 1)
    {
        int a = heap.top(); heap.pop();
        int b = heap.top(); heap.pop();
        
        res += a + b;
        heap.push(a + b);
    }
    
    cout << res << endl;
    
    return 0;
}