数字三角形
问题描述
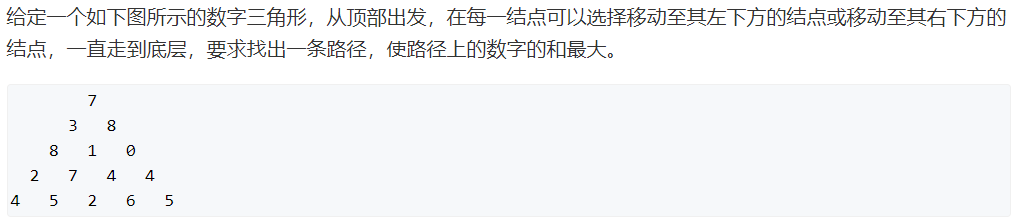
问题分析
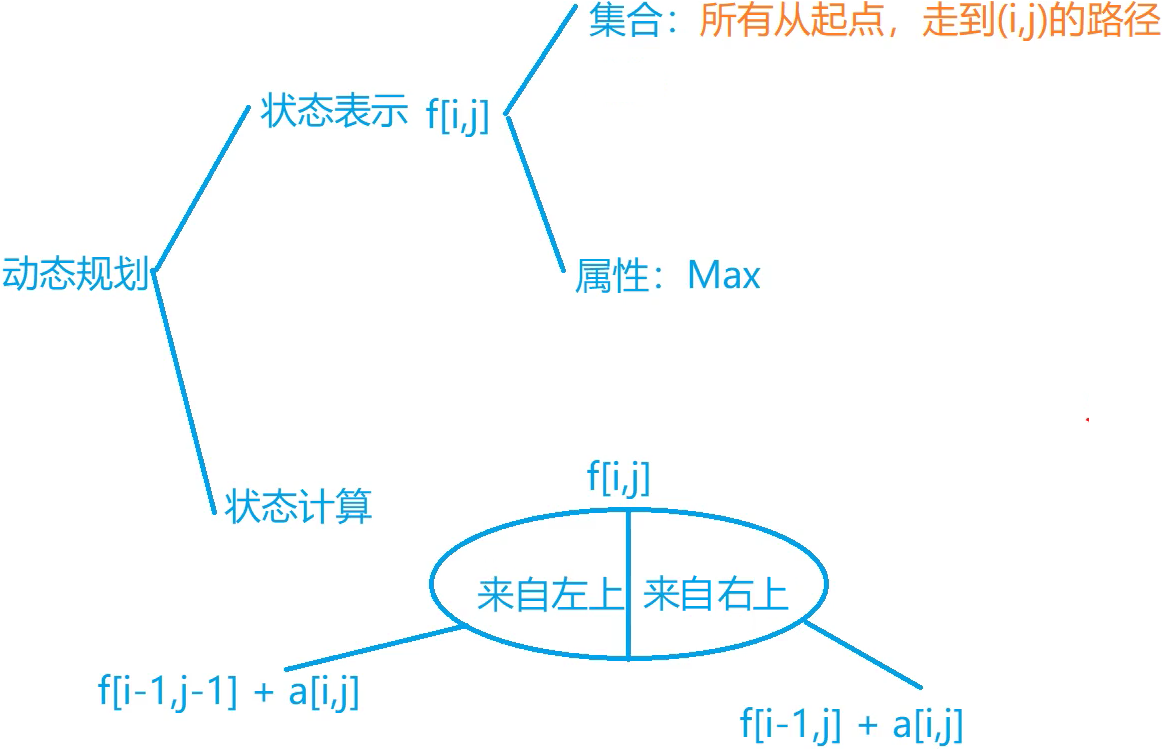
代码实现-从上到下
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int n;
int a[N][N];
int main()
{
cin >> n;
// 初始化是个坑点,左右两侧都需要多初始化一个
for (int i = 0; i <= n; ++ i)
for (int j = 0; j <= i + 1; ++ j)
a[i][j] = -INF;
cin >> a[1][1];
for (int i = 2; i <= n; ++ i)
for (int j = 1; j <= i; ++ j)
{
cin >> a[i][j];
a[i][j] += max(a[i - 1][j - 1], a[i - 1][j]);
}
int res = -INF;
for (int i = 1; i <= n; ++ i)
res = max(res, a[n][i]);
cout << res << endl;
return 0;
}
代码实现-从下到上
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int n;
int a[N][N];
int main()
{
cin >> n;
for (int i = 1; i <= n; ++ i)
for (int j = 1; j <= i; ++ j)
cin >> a[i][j];
for (int i = n; i >= 1; -- i)
for (int j = 1; j <= i; ++ j)
a[i][j] += max(a[i + 1][j], a[i + 1][j + 1]);
cout << a[1][1] << endl;
return 0;
}
最长上升子序列Ⅰ
问题描述
给定一个长度为N的数列,求数值严格单调递增的子序列的长度最长是多少。
(1 leq N leq 1000)
问题分析
在状态计算时,需要把集合f[i]按照前一位是哪个数字划分,从而根据(f[i] = max(f[j] + 1), j = 1、2、3、... i-1)进行计算
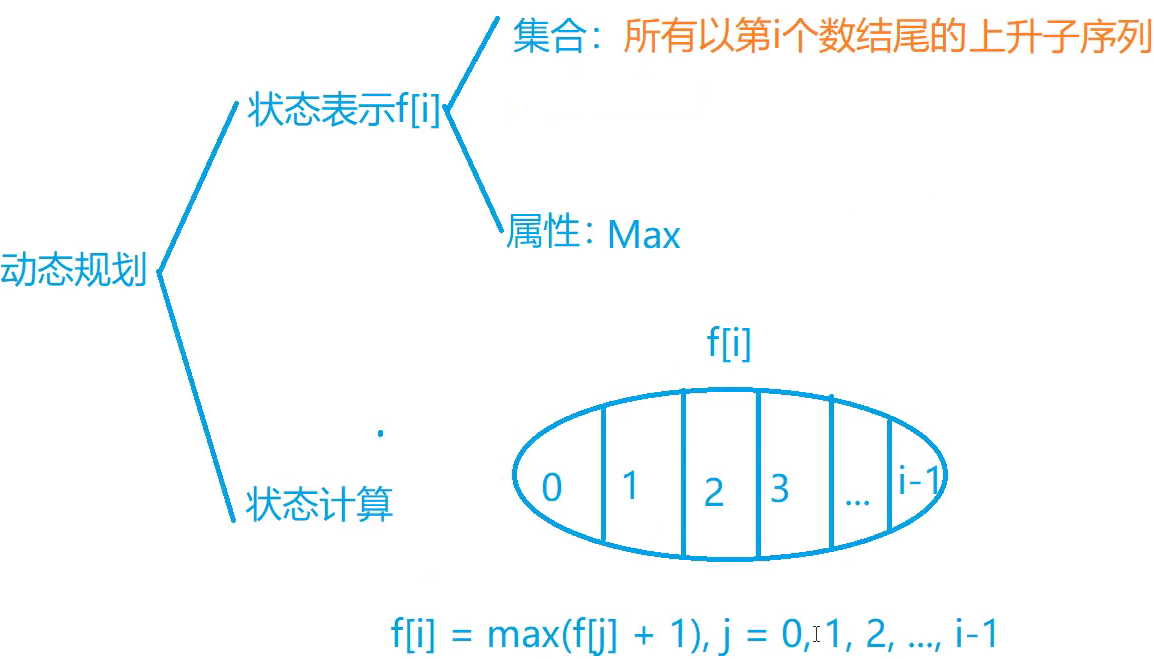
代码实现
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int a[N], f[N];
int main()
{
cin >> n;
for (int i = 1; i <= n; ++ i)
cin >> a[i];
for (int i = 1; i <= n; ++ i)
{
f[i] = 1;
for (int j = 1; j < i; ++ j)
if (a[j] < a[i])
f[i] = max(f[i], f[j] + 1);
}
int res = 0;
for (int i = 1; i <= n; ++ i)
res = max(res, f[i]);
cout << res << endl;
return 0;
}
最长上升子序列Ⅱ
由于数据范围的变化,解题方法也发生了根本性的改变,准确的说此时的问题已经不能看为动态规划问题了
问题描述
给定一个长度为N的数列,求数值严格单调递增的子序列的长度最长是多少。
(1 leq N leq 100000)
问题分析
根据分析,可以得到以下两条性质
1.
对于相同长度的上升子序列,仅需要留存结尾数值最小的那一个。
对于序列3214,考虑以4结尾的最长上升子序列,以它前面所有数据结尾的最长上升子序列的长度均为1,按照之前的做法,我们需要判断3次,但很明显,我们只需要判断1。对于321后面的所有数据,都仅仅需要考虑1,因为对于后面数据来说,选择1要比选择2和3具有更多的可能性,是更优的选择。
2.
随着上升序列长度的增加,结尾数值一定严格递增
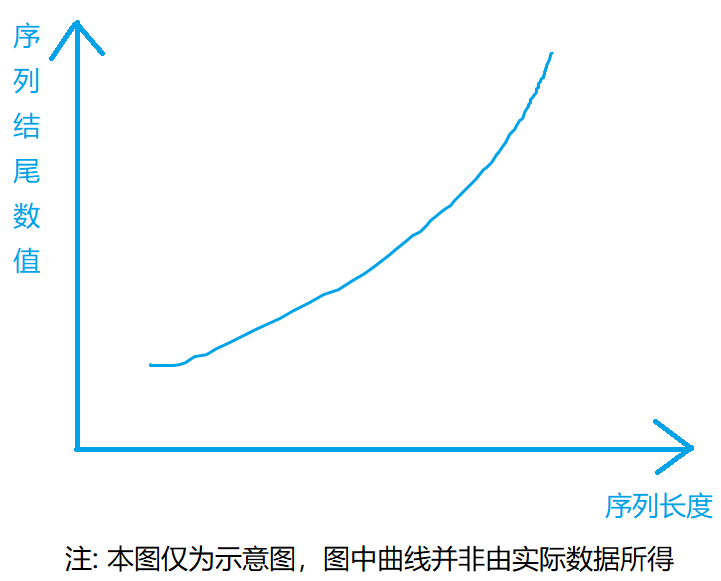
证明采用反证法。假设目前找到的长度为5和6的上升子序列结尾数值相等(分别对应1点和2点),根据1点,我们显然可以得到一个a点,该点满足以它结尾的上升序列长度为5,且a点数值小于1点。该点的存在显然和2点发生了矛盾,所以我们的假设不成立,同理可证,“假设长度为5的上升子序列结尾数值小于长度为6的”也是不成立的。综上所述,性质得证。
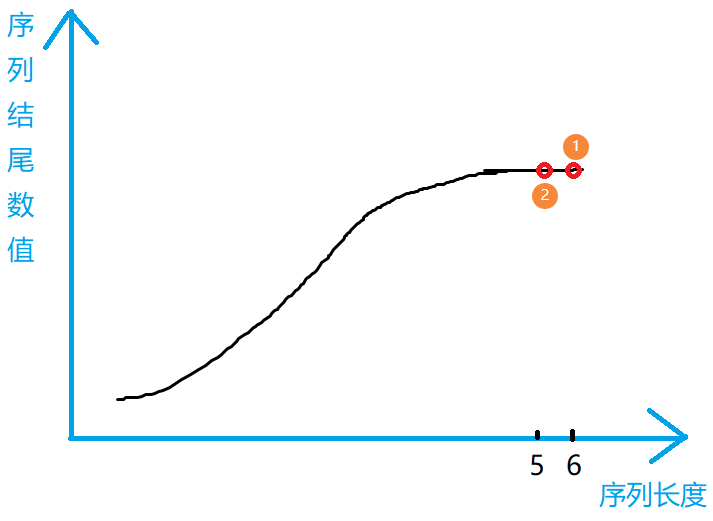
根据性质1,我们能够去掉一些无效判断。但是在代码实现时,对于序列中的某个数值a,它的前面包含各种长度的序列,如果我们遍历所有长度的序列找到其中结尾数值小于a且最接近a的序列,复杂度并没有发生改变。但是由于性质2的存在,我们采用对序列长度进行二分即可找到最优的解,这是由于序列长度和序列结尾数值之间存在单调性,我们的目标是找到正确的序列长度,但是判断是否正确的依据是序列结尾数值的大小,两者间的单调性完美解决了这一问题。
代码实现
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;//, INF = 0x7f7f7f7f;
int n;
int a[N], q[N]; // q[i]: 长度为i的上升子序列的最优结尾数值
int main()
{
cin >> n;
for (int i = 1; i <= n; ++ i)
cin >> a[i];
// memset(q, 0x7f, sizeof q);
int len = 0;
for (int i = 1; i <= n; ++ i)
{
// 找到结尾数值小于a[i]且最接近a[i]的上升子序列,根据性质2,此时的长度是最优的
int l = 0, r = len; // 321中的每个数前面显然都是没有答案的,对应的长度是0,即0也可能是答案
while (l < r)
{
int mid = l + r + 1>> 1;
if (q[mid] < a[i]) l = mid;
else r = mid - 1;
}
len = max(len, l + 1);
q[l + 1] = a[i];
// q[l + 1] = min(q[l + 1], a[i]);
/**
* 第一次这里之所以这样写是因为我担心两次出现相同长度的值,应该保留更小的结尾数值
* 但实际上 q[l + 1] = a[i] 这样写就没错,
* 假设之前出现过一次l+1, 后面又出现一次相等的l+1,为什么能够保证后面的一定是更小的呢
* 因为假设后面的更大,那么这个序列就不是这个长度了
* 假设xxxa 和 xxxb,a在b之前,如果b>a,那么xxxb就不是以b结尾的最长上升子序列,因为前面还需要包含一个a
*/
}
cout << len << endl;
return 0;
}
最长公共子序列
问题描述
给定两个长度分别为N和M的字符串A和B,求既是A的子序列又是B的子序列的字符串长度最长是多少
问题分析
f[i][j]的划分需要按照字符串A的A[i]和字符串B的B[j]两个字符是否一定包含在公共序列中
- 下图中的00表示
a[i]和b[j]均不包含在字符串S中(S表示在A的前i个字母出现,且在B的前j个字母中出现的子序列,下同) - 01表示
a[i]不包含在S中,b[j]包含在S中 - 10表示
a[i]包含在S中,b[j]不包含在S中 - 11表示
a[i]包含在S中,b[j]包含在S中(a[i]和b[j]出现在相同的子序列中且两者均位于最后一个字符则必须保证两者相同)
通过以上四种分法保证能够覆盖到f[i][j]的所有情况
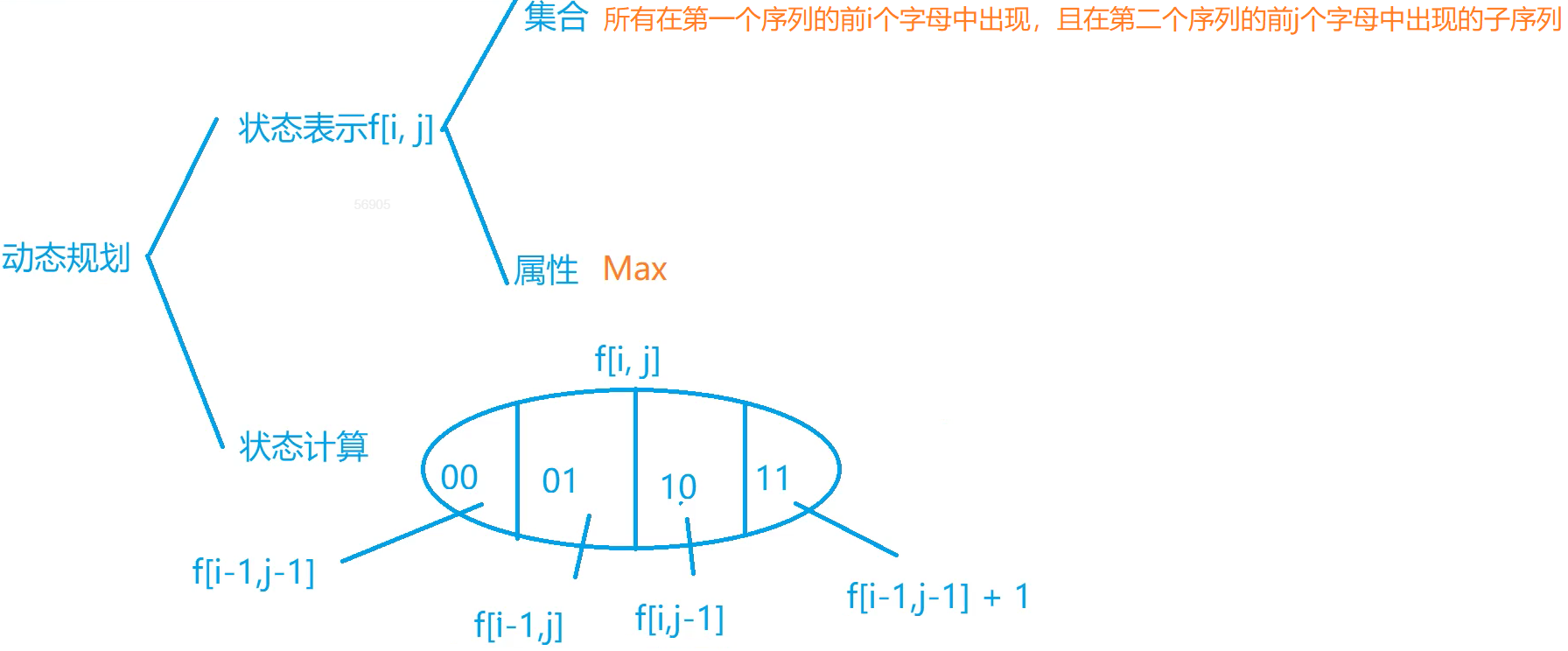
需要注意上图中的f[i - 1][j],f[i][j - 1]并不能分别准确表示上述01和10代表的含义。f[i - 1][j]表示的真正含义为“所有在A的前i-1个字母中出现且在B的前j个字母中出现的子序列”,这样并不能保证子序列中一定包含b[j],但有可能包含b[j],即其表示的范围要大于我们实际需要的01的范围。同理f[i][j - 1]的表示范围也要大于10所需的范围。但是这样对答案的求解并没有影响,因为我们求解的最大值,重复数据并不会影响到最终结果。而且这两者的并集已经包含了f[i - 1][j - 1],所以代码实现时不需要再考虑f[i - 1][j - 1]了。
代码实现
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main()
{
cin >> n >> m;
cin >> a + 1 >> b + 1;
for (int i = 1; i <= n; ++ i)
for (int j = 1; j <= m; ++ j)
{
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if (a[i] == b[j]) // 如果保证a[i] 和 b[j] 都一定选,那么两者必须保证相等
f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
}
cout << f[n][m] << endl;
return 0;
}
最短编辑距离
问题描述
给定两个字符串A和B,现在要将A经过若干操作变为B,可进行的操作有:
- 删除–将字符串A中的某个字符删除
- 插入–在字符串A的某个位置插入某个字符
- 替换–将字符串A中的某个字符替换为另一个字符
现在请你求出,将A变为B至少需要进行多少次操作
问题分析
f[i][j]代表的既然是所有操作方式,那么划分的方式自然是按照操作方式进行
同时根据字符串dp的相关问题的解法,一般考虑最后一个字母的情况
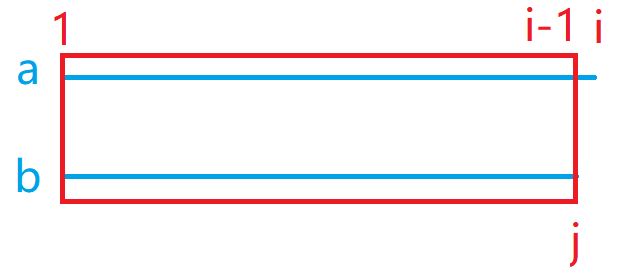
- 如果将
a[1~i]变为b[1~j]采用的方式是删除a的最后一个字母,那么将a[1~i]变为b[1~j]的最少操作次数为f[i - 1][j] + 1,即将a[1~i-1]变为b[1~j]的次数再加上删除最后一个字母
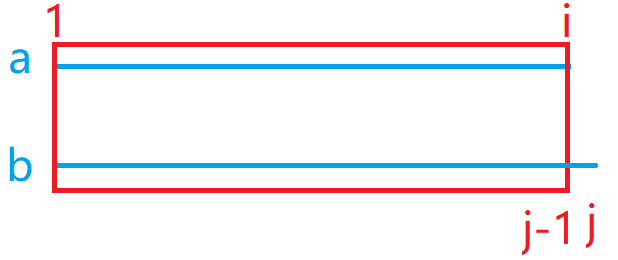
- 如果将
a[1~i]变为b[1~j]采用的方式是在a的最后增加一个字母,最少操作次数为f[i][j - 1] + 1,即将a[1~i]变为b[1~j-1]的次数再加上增加最后一个字母
- 如果将
a[1~i]变为b[1~j]采用的方式是修改a的最后一个字母,此时有两种情况:- 1.
a[i]==b[j]:此时最少操作次数为f[i-1][j-1],最后一位相同不需要改,只需要把前i-1和j-1位修改为相同即可 - 2.
a[i]!=b[j]:此时最少操作次数为f[i-1][j-1] + 1,即把前i-1和j-1位修改为相同并加上最后一次的修改
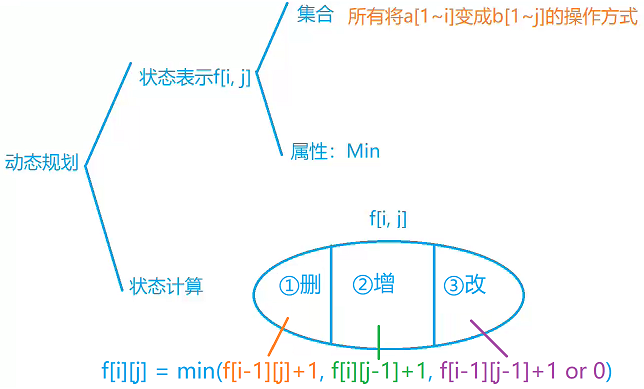
- 1.
代码实现
代码实现需要关注初始化,此前不需要单独初始化是因为需要的初始值恰好为0,但这里初始值不再为0
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main()
{
cin >> n;
cin >> a + 1;
cin >> m;
cin >> b + 1;
// 关注这里的初始化
for (int i = 0; i <= m; ++ i) f[0][i] = i;
for (int i = 0; i <= n; ++ i) f[i][0] = i;
for (int i = 1; i <= n; ++ i)
for (int j = 1; j <= m; ++ j)
{
f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
if (a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]);
else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
}
cout << f[n][m] << endl;
return 0;
}