组合数

预处理结果

问题类型

n组查询：(1 leq n leq 10^4)
每次查询(C_a^b) : (1 leq b leq a leq 2000)
如果按照公式计算，最坏时间复杂度是O(n * b)，当n取(10^4)，a 和 b取 (10^5) 时，总运算次数为 (10^4 * 2 * 10^5 = 2 * 10^9)

算法原理及流程

根据公式 (C_a^b = c_{a - 1}^b + C_{a - 1}^{b - 1}) 进行递推

代码实现

#include <iostream>

using namespace std;

const int N = 2010, mod = 1e9 + 7;

int n;
int c[N][N];

void init()
{
    for (int i = 0; i < N; ++ i)
        for (int j = 0; j <= i; ++ j) // 注意这里要求j<=i，所以能够处理所有边界情况。从实际意义上来将，从i个物品中选，最多选择i个，同样能够表示j的范围的意义
            if (!j) c[i][j] = 1; // c_i^0都等于0
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}
int main()
{
    init();
    cin >> n;
    while (n --)
    {
        int a, b;
        cin >> a >> b;
        cout << c[a][b] << endl;
    }
    return 0;
}

预处理阶乘和逆元

问题类型

n组查询：(1 leq n leq 10^4)
每次查询(C_a^b) : (1 leq b leq a leq 10^5)
之所以不能预处理结果，是因为a和b的范围过大，用数组下标已经存不下了

算法原理及流程

预处理阶乘和阶乘的逆元。由于根据公式计算涉及到除法，所以取模需要用到逆元

代码实现

解释一下代码中计算阶乘的逆元时的两种写法等价的原因：((k!)^{-1} = (k!)^{mod - 2} = ((k - 1)! * k)^{mod - 2} = ((k - 1)!)^{mod - 2} * (k)^{mod - 2} = ((k - 1)!)^{-1} * (k)^{-1})

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10, mod = 1e9 + 7;

int n;
LL fact[N], infact[N]; // fact[i]:i的阶层 infact[i]:i的阶乘的逆元

int qpow(int a, int b, int mod)
{
    int res = 1;
    while (b)
    {
        if (b & 1) res = (LL)res * a % mod;
        a = (LL)a * a % mod;
        b >>= 1;
    }
    return res;
}
void init()
{
    fact[0] = infact[0] = 1;
    for (int i = 1; i < N; ++ i) 
    {
        fact[i] = (LL)fact[i - 1] * i % mod;
        infact[i] = qpow(fact[i], mod - 2, mod); // 因为mod是一个质数，所以可以使用费马小定理计算逆元
        // 或者 infact[i] = (LL)infact[i - 1] * qpow(i, mod - 2, mod); 原因见上
    }
}
int main()
{
    init();
    cin >> n;
    while (n --)
    {
        int a, b;
        cin >> a >> b;
        cout << ((LL)fact[a] * infact[b] % mod * infact[a - b] % mod) << endl;
        // 两个大int可能会爆long long，所以需要先%一下
    }
    return 0;
}

卢卡斯优化

问题类型

n组查询：(1 leq n leq 20)
每次查询(C_a^b) : (1 leq b leq a leq 10^{18})
mod p: (1 leq p leq 10^5)
查询次数不多；该类型具有一个很明显的特征就是 (C_a^b)中的a和b都是大于模数p的，所以可以采用卢卡斯定理进行优化

算法原理及流程

卢卡斯(lucas)定理：(C_a^b equiv C_{a / p}^{b / p} * C_{a \% p}^{b \% p} pmod {p})

首先调用卢卡斯定理进行优化，然后直接使用公式进行计算，除法取模需要求逆元

代码实现

#include <iostream>

using namespace std;

typedef long long LL;

int n;

int qpow(int a, int b, int p)
{
    int res = 1;
    while (b)
    {
        if (b & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        b >>= 1;
    }
    return res;
}
int c(int a, int b, int p) // 调用组合数时候就一定保证a和b是小于p的了，所以a和b定为int
{
    if (b > a) return 0;
    
    // 按照公式计算
    int res = 1;
    for (int i = a - b + 1, j = 1; j <= b; ++ i, ++ j)
    {
        res = (LL)res * i % p;
        // 保证b是小于p的，因为p质数，所以1到b的所有数都一定与p互质，所以计算逆元可以采用费马小定理
        res = (LL)res * qpow(j, p - 2, p) % p; // 理解原理需要用到“预处理中间值-代码实现”中提到的等式
    }
    
    return res;
}
int lucas(LL a, LL b, int p)
{
    if (a < p && b < p) return c(a, b, p);
    return (LL)c(a % p, b % p, p) * lucas(a / p, b / p, p) % p; // %p保证运算后的结果小于p，无法再使用lucas优化了，所以直接调用组合式函数即可，但/运算则无法保证
}
int main()
{
    cin >> n;
    while (n --)
    {
        int p;
        LL a, b;
        cin >> a >> b >> p;
        
        cout << lucas(a, b, p) << endl;
    }
    return 0;
}

质因数分解

问题类型

计算结果不能取模，结果可能很大
对于(c_a^b)，我们只需筛选出(<=a)的所有质因子即可，因为根据下方介绍的计算公式，我们计算的是(1)到(n)中质因子(p)的个数，当(p>n)时，其个数一定为(0)，没有计算的必要了

算法原理及流程

原理
很明显的是，结果很大需要用高精度，如果单纯通过公式进行计算，(c_a^b = frac{(a - b + 1) * ... * a}{1 * ... * b})，需要用到高精度乘法和除法，整起来就有些复杂了，所以考虑将(C_a^b) 转化为 $ p_1^{k_1} * p_2^{k_2} * ... * p_n^{k_n} $，，从而将运算转变为单纯的乘法。
如果对公式 (c_a^b = frac{(a - b + 1) * ... * a}{1 * ... * b}) 中的每个数进行一次质因数分解，复杂度就是 (O(n sqrt[2]{n}))，估计也没什么大问题，但是代码写起来还是有点复杂的，所以这里利用一个很神奇的计算方法：

a! 中 质因子 p 的个数为 (lfloor frac{a}{p} floor + lfloor frac{a}{p^2} floor + ... + lfloor frac{a}{p^n} floor).

这里的(lfloor frac{a}{p} floor)具有一个特定的含义

1到n中p的倍数(或者说能被p整除)的数有 (lfloor frac{n}{p} floor) 个(该性质的详细描述请参照 倍数个数的计算)

根据(lfloor frac{n}{p} floor)的含义，(lfloor frac{n}{p} floor) 计算的为1到n中p的倍数个数； (lfloor frac{n}{p^2} floor) 计算的为1到n中(p^2)的倍数个数。。。以此类推
将这些倍数个数相加，计算得出的就是1到n的所有数中质因子p所占据的个数。
不妨举个例子来理解这个方法，计算6！中质因子2的个数: (6! = 1 * 2 * 3 * 4 * 5 * 6), 其中2，4，6是2的倍数，4是(2^2)的倍数，而2，6对质因子2个数的贡献值为1，4的贡献值为2。4中有两个2，在(lfloor frac{a}{p} floor)时考虑到的是它其中一个2，(lfloor frac{a}{p^2} floor)考虑的则是另一个2。也就是说1到6的所有数，2的倍数有3个，(2^2)的倍数有1个，所以1到6中所有数中质因子2的个数为4个。

流程
(C_a^b = frac{a!}{b! * (a - b)!}),我们首先预处理出所有质因子，然后分别计算出所有质因子的个数，最后调用高精度乘法计算得出最后结果

代码实现

#include <iostream>
#include <vector>

using namespace std;

const int N = 5010;

int sum[N];
int primes[N], cnt;
bool st[N];

vector<int> mul(vector<int> &a, int b) // 高精度乘法
{
    vector<int> c;
    
    int t = 0;
    for (int i = 0; i < a.size() || t; ++ i)
    {
        if (i < a.size()) t += a[i] * b;
        c.push_back(t % 10);
        t /= 10;
    }
    while (c.size() != 1 && c.back() == 0) c.pop_back();
    
    return c;
}

void get_primes(int n) // 打素数表
{
    st[0] = st[1] = true;
    for (int i = 2; i <= n; ++ i)
    {
        if (!st[i]) primes[cnt ++]  = i;
        for (int j = 0; primes[j] <= n / i; ++ j)
        {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) break;
        }
    }
}
int get(int a, int p) // 返回a!中质因子p的个数
{
    int res = 0;
    while (a)
    {
        res += a / p;
        a /= p;
    }
    return res;
}

int main()
{
    int a, b;
    cin >> a >> b;
    
    // 预处理质数表
    get_primes(a);
    
    // 计算公式中每个质数的个数
    for (int i = 0; i < cnt; ++ i)
    {
        int p = primes[i];
        sum[i] = get(a, p) - get(b, p) - get(a - b, p);
    }
    
    // 高精度乘法计算最终结果
    vector<int> res;
    res.push_back(1);
    
    for (int i = 0; i < cnt; ++ i)
        for (int j = 0; j < sum[i]; ++ j)
            res = mul(res, primes[i]);
    
    // 输出答案
    for (int i = res.size() - 1; ~i; -- i) cout << res[i];
    cout << endl;
    
    return 0;
}

应用

计算卡特兰数(Catalan)

该类问题的难点在于如何将实际问题抽象为求解卡特兰数，而非代码实现

公式推导

下面以一个例子说明卡特兰数的公式是如何推导的

给定n个0和n个1，它们将按照某种顺序排成长度为2n的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中0的个数都不少于1的个数的序列有多少个

问题分析
需要把问题变为一个几何问题，在一个网格图中，类似哈夫曼编码，我们规定 向右走为0，向上走为1
假设分别有6个0和1，任意一个序列如果映射到网格图中，就是一条从(0, 0)到(6, 6)的路径，0的数量代表着横坐标的值，1的数量代表纵坐标的值，所以满足要求的序列就是保证路径上任意一个点的横坐标>=纵坐标，也就是说从(0, 0)到(6, 6)的直线下方的路径才是合法路径，合法序列数量等价为合法路径数量，也就是我们需要求解的从(0, 0)到(6, 6)且不经过对角线的路径总数
求解
按照公式合法方案数 = 总方案数 - 非法方案数，总方案数 = (C_{12}^6)，问题的难点在于如何求解非法方案数。观看下图，我们首先画出一条非法的路径，交对角线于1号点，将非法路径中1号点之后的路径关于对角线做对称可以得到3号线到(5, 7)。很神奇的是不管1号点在哪里，3号线的终点都是(5, 7)(我没想明白为什么)。也就是说任意一条从(0, 0)到(6, 6)的非法路径都可以等价为从(0, 0)到(5, 7)的路径，所以非法路径数 = (C_{12}^5) 或 (C_{12}^7)。

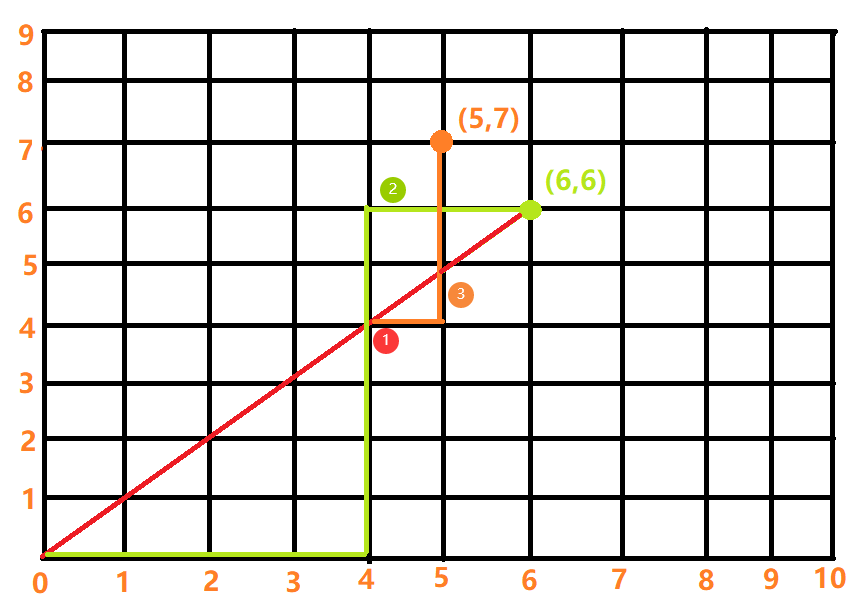
将上述描述总结为公式就是：(C_{2n}^{n} - C_{2n}^{n - 1} = frac{C_{2n}^{n}}{n + 1}) 或 (C_{2n}^{n} - C_{2n}^{n + 1} = frac{C_{2n}^{n}}{n + 1})，但一般都记前面那个式子

代码实现

只需要按照公式计算即可，实际采用的是卢卡斯优化代码中组合数的求解方法

#include <iostream>

using namespace std;

typedef long long LL;

const int mod = 1e9 + 7;

int qpow(int a, int b, int mod)
{
    int res = 1;
    while (b)
    {
        if (b & 1) res = (LL)res * a % mod;
        a = (LL)a * a % mod;
        b >>= 1;
    }
    return res;
}
int main()
{
    int n;
    cin >> n;
    
    int res = 1;
    for (int i = n + 1, j = 1; j <= n; ++ i, ++ j)
    {
        res = (LL)res * i % mod;
        res = (LL)res * qpow(j, mod - 2, mod) % mod;
    }
    
    res = (LL)res * qpow(n + 1, mod - 2, mod) % mod;
    
    cout << res << endl;
    return 0;
}