免费馅饼
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 62694 Accepted Submission(s): 21961
Problem Description
都说天上不会掉馅饼,但有一天gameboy正走在回家的小径上,忽然天上掉下大把大把的馅饼。说来gameboy的人品实在是太好了,这馅饼别处都不掉,就掉落在他身旁的10米范围内。馅饼如果掉在了地上当然就不能吃了,所以gameboy马上卸下身上的背包去接。但由于小径两侧都不能站人,所以他只能在小径上接。由于gameboy平时老呆在房间里玩游戏,虽然在游戏中是个身手敏捷的高手,但在现实中运动神经特别迟钝,每秒种只有在移动不超过一米的范围内接住坠落的馅饼。现在给这条小径如图标上坐标:

为了使问题简化,假设在接下来的一段时间里,馅饼都掉落在0-10这11个位置。开始时gameboy站在5这个位置,因此在第一秒,他只能接到4,5,6这三个位置中其中一个位置上的馅饼。问gameboy最多可能接到多少个馅饼?(假设他的背包可以容纳无穷多个馅饼)
Input
输入数据有多组。每组数据的第一行为以正整数n(0<n<100000),表示有n个馅饼掉在这条小径上。在结下来的n行中,每行有两个整数x,T(0<T<100000),表示在第T秒有一个馅饼掉在x点上。同一秒钟在同一点上可能掉下多个馅饼。n=0时输入结束。
Output
每一组输入数据对应一行输出。输出一个整数m,表示gameboy最多可能接到m个馅饼。
提示:本题的输入数据量比较大,建议用scanf读入,用cin可能会超时。
Sample Input
6
5 1
4 1
6 1
7 2
7 2
8 3
0
Sample Output
4
思路
找出输入的最大时间,从最大时间下开始向前找能接到的最多的馅饼数。最后输出时间为0,位置为5的馅饼数。
状态转移方程:dp[i][j]=max(dp[i+1][j+1],max(dp[i+1][j],dp[i+1][j-1]))
实现过程:
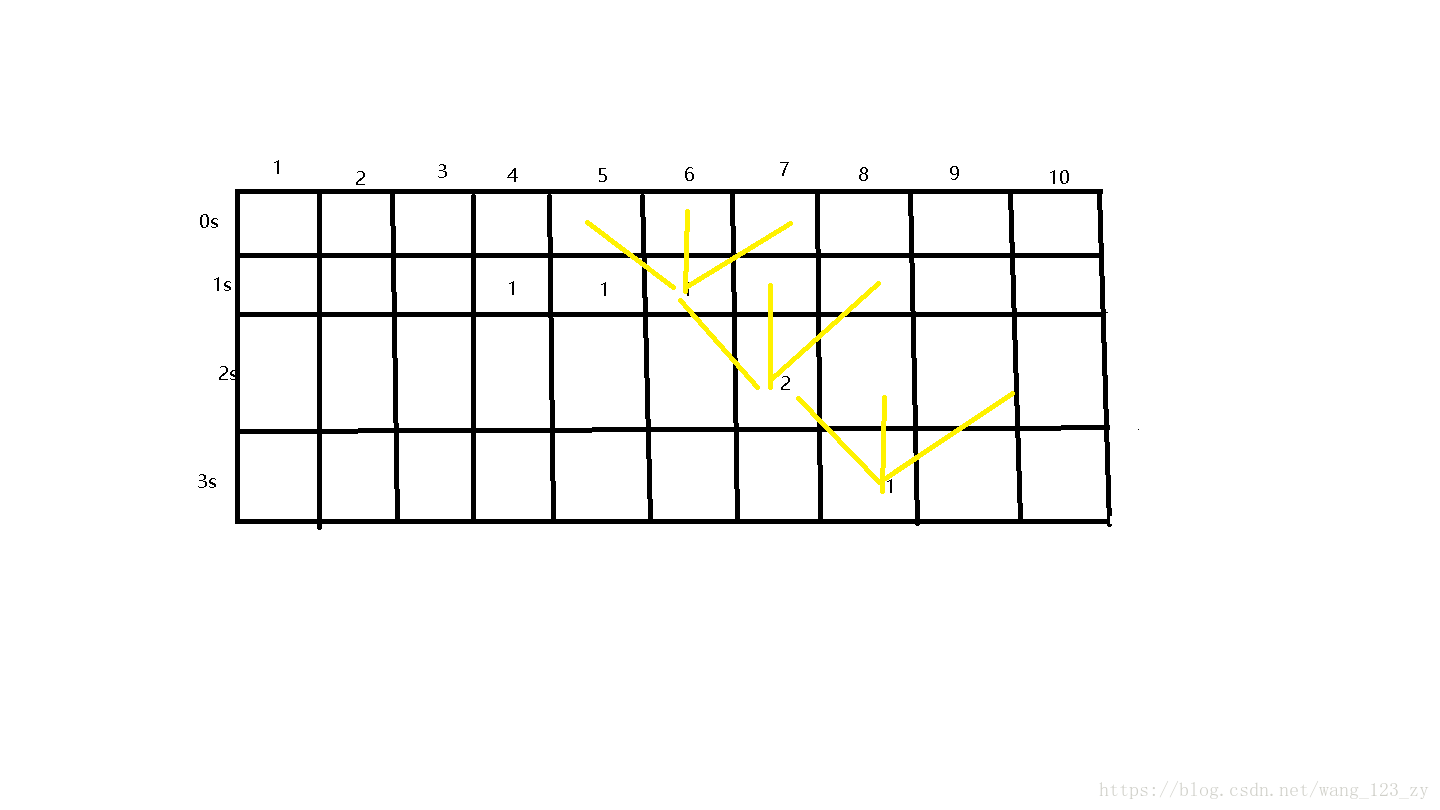
该题样例可以建立成一个二维矩阵,如图所示
那么从最后一行开始,因为每个点在每秒有三种可能走的情况,所以要记录下走到某点时拿到馅饼数的最大值。每次dp[i][j]都会在本身的基础上加上dp[i+1][j+1],dp[i+1][j],dp[i+1][j-1]这三者的最大值
如:在开始的时候,dp[3][8]=1,dp[2][7]=2 。在状态转移后,倒数第二行的元素变成了
| 0 | 0 | 0 | 0 | 0 | 0 | 3 | 1 | 1 | 0 |
继续往前走,倒数第三行(第1s的那一行)各元素变成了
| 0 | 0 | 0 | 1 | 1 | 4 | 3 | 3 | 0 | 0 |
到第一行(第0s)
| 0 | 0 | 1 | 1 | 4 | 4 | 4 | 3 | 3 | 0 |
这时候输出起始位置dp[0][5]的值就可以了
AC代码
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <math.h>
#include <limits.h>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#include <set>
#include <string>
#define ll long long
#define ms(a) memset(a,0,sizeof(a))
#define pi acos(-1.0)
#define INF 0x3f3f3f3f
const double E=exp(1);
const int maxn=1e5+10;
using namespace std;
int dp[maxn][20];
int main(int argc, char const *argv[])
{
// 状态转移方程:dp[i]=max(dp[i+1][j+1],max(dp[i+1][j-1],dp[i+1][j]))
int n;
while(~scanf("%d",&n)&&n)
{
ms(dp);
int res=0;
int place,time;
for(int i=0;i<n;i++)
{
scanf("%d%d",&place,&time);
dp[time][place]++;
res=max(res,time);
}
for(int i=res;i>=0;i--)
{
for(int j=0;j<11;j++)
{
dp[i][j]+=max(dp[i+1][j-1],max(dp[i+1][j+1],dp[i+1][j]));
}
}
printf("%d
",dp[0][5]);
}
return 0;
}