Description
(Seter)建造了一个很大的星球,他准备建造(N)个国家和无数双向道路。(N)个国家很快建造好了,用(1..N)编号,但是他发现道路实在太多了,他要一条条建简直是不可能的!于是他以如下方式建造道路:((a,b),(c,d))表示,对于任意两个国家x,y,如果(aleq xleq b,cleq yleq d),那么在(x,y)之间建造一条道路。(Seter)保证一条道路不会修建两次,也保证不会有一个国家与自己之间有道路。
(Seter)好不容易建好了所有道路,他现在在位于(P)号的首都。(Seter)想知道(P)号国家到任意一个国家最少需要经过几条道路。当然,(Seter)保证(P)号国家能到任意一个国家。
Input
第一行三个数(N,M,P)。(Nleq 500000,Mleq 100000)。
后M行,每行4个数(A,B,C,D)。(1leq Aleq Bleq N,1leq Cleq Dleq N)。
Output
(N)行,第(i)行表示(P)号国家到第(i)个国家最少需要经过几条路。显然第(P)行应该是0。
Sample Input
5 3 4
1 2 4 5
5 5 4 4
1 1 3 3
Sample Output
1
1
2
0
1
solution
一个显然的暴力思路就是一个个点连边。但是这样大数据一定裂开。我们考虑线段树优化建边(线段树可以完成区间操作,题目给出的就是一整个区间,对于线段树来说是非常友好的)。
线段树优化建边
我们定义:
进树:一颗线段树从父亲到儿子连边权为0的边
出树:一颗线段树从儿子到父亲连边权为0的边
超级点:既不属于进树也不属于出树,用于连接进树与出树的点
那么我们对于每一个要连的区间((a,b),(c,d))都先将出树中对应区间连边权为0的有向边到超级点,再从超级点连边权为1的有向边到进树中,这里需要两个超级点,如果用同一个超级点的话,会有原来不能互相到达的点却互相到达的情况。
大概如图:图源
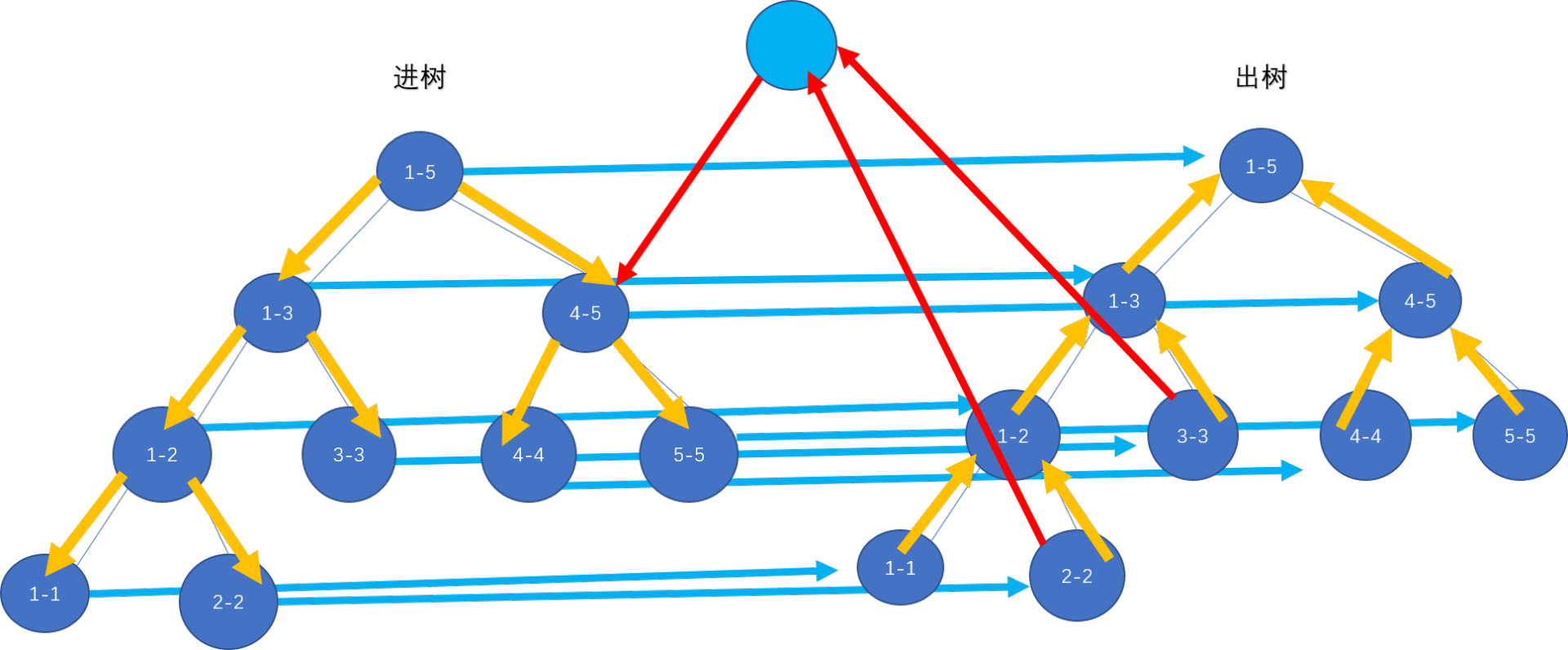
为什么要从进树连边到出树?因为从给定的起点出发可能需要经过别的点才能到某些点。
剩下的就是一个简单的(dijkstra)啦
Code
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#define mk make_pair
#define lc k<<1
#define rc k<<1|1
using namespace std;
const int N=5e5+5,M=1e7+5;
struct E {
int to,nxt,w;
}e[N*30];
int n,m,p,head[M],cnt,tot,sup,vis[M],dis[M];
inline int read () {
int res=0,fl=1;
char ch;
while ((ch=getchar())&&(ch<'0'||ch>'9')) if (ch=='-') fl=-1;
res=ch^48;
while ((ch=getchar())&&ch>='0'&&ch<='9') res=(res<<1)+(res<<3)+(ch^48);
return res*fl;
}
inline void add (int x,int y,int z) {
e[++cnt]=(E){y,head[x],z};
head[x]=cnt;
}
struct node {
int tre[N<<2];
inline void build (int k,int l,int r,int ty) {
tre[k]=++tot;
if (l==r) return;
int mid=(l+r)>>1;
build(lc,l,mid,ty);
build(rc,mid+1,r,ty);
if (ty==0) add(tre[k],tre[lc],0),add(tre[k],tre[rc],0);
else add(tre[lc],tre[k],0),add(tre[rc],tre[k],0);
}
inline void update (int k,int l,int r,int x,int y,int v,int ty) {
if (x<=l&&r<=y) {
if (ty) add(tre[k],sup,v);
else add(sup,tre[k],v);
return;
}
int mid=(l+r)>>1;
if (x<=mid) update(lc,l,mid,x,y,v,ty);
if (y>mid) update(rc,mid+1,r,x,y,v,ty);
}
inline int get (int k,int l,int r,int x) {
if (l==r&&l==x) return tre[k];
int mid=(l+r)>>1;
if (x<=mid) return get(lc,l,mid,x);
else return get(rc,mid+1,r,x);
}
}t_in,t_out;
inline void build2 (int k,int l,int r) {
add(t_in.tre[k],t_out.tre[k],0);
if (l==r) return;
int mid=(l+r)>>1;
build2(lc,l,mid);
build2(rc,mid+1,r);
}
inline void dijkstra (int st) {
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
memset(dis,0x3f,sizeof(dis));
dis[st]=0;
q.push(mk(dis[st],st));
while (!q.empty()) {
int x=q.top().second;
q.pop();
if (vis[x]) continue;
vis[x]=1;
for (int i=head[x];i;i=e[i].nxt) {
int v=e[i].to;
if(vis[v]) continue;
if (dis[v]>dis[x]+e[i].w) {
dis[v]=dis[x]+e[i].w;
q.push(mk(dis[v],v));
}
}
}
}
inline void print (int k,int l,int r) {
if (l==r) {
printf("%d
",dis[t_in.tre[k]]);
return;
}
int mid=(l+r)>>1;
print(lc,l,mid);
print(rc,mid+1,r);
}
int main () {
#ifndef ONLINE_JUDGE
freopen("3073.in","r",stdin);
freopen("3073.out","w",stdout);
#endif
n=read();m=read();p=read();
// cout<<n<<" "<<m<<" "<<p<<endl;
t_in.build(1,1,n,0);
// cout<<"*"<<tot<<endl;
t_out.build(1,1,n,1);
sup=tot;
// cout<<"!"<<tot<<endl;
for (int i=1,a,b,c,d;i<=m;i++) {
a=read();b=read();c=read();d=read();
sup++;
t_in.update(1,1,n,a,b,1,0);
t_out.update(1,1,n,c,d,0,1);
sup++;
t_in.update(1,1,n,c,d,1,0);
t_out.update(1,1,n,a,b,0,1);
}
build2(1,1,n);
// cout<<"!"<<endl;
// int pos=t_out.get(1,1,n,p);
int pos1=t_in.get(1,1,n,p);
// add(pos,pos1,0);
// cout<<pos<<endl;
dijkstra(pos1);
print(1,1,n);
return 0;
}