题目链接:https://ac.nowcoder.com/acm/contest/992/A
题意:求出长度为n的字符串个数,字符串由A、C、G、T组成,其中A和C必须成对出现。
思路:我们规定: f[n][0]--长度为n的合法字符串个数
f[n][1]--长度为n的A为奇数个的字符串个数
f[n][2]--长度为n的C为奇数个的字符串个数
f[n][3]--长度为n的A、C均为奇数个的字符串个数
那么有如下转移方程:
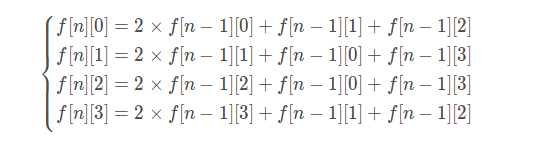
根据转移方程构建矩阵:

就可以通过矩阵快速幂求得了,n太大了,继续思考:

然后齐次线性递推得到:f[n][0]=4n-1+2n-1,之后欧拉降幂即可。
AC代码:
#include<cstdio> #include<algorithm> #include<cstring> using namespace std; typedef long long LL; const int MOD=1e9+7; const int MOD1=1e9+6; char s[100005]; LL qpow(LL a,LL b){ LL ret=1; while(b){ if(b&1) ret=ret*a%MOD; a=a*a%MOD; b>>=1; } return ret; } int main(){ while(~scanf("%s",s)){ LL tmp=0; for(int i=0;i<strlen(s);++i) tmp=(tmp*10+s[i]-'0')%MOD1; if(tmp>0) --tmp; else tmp=MOD1-1; tmp=qpow(2,tmp); printf("%lld ",tmp*(tmp+1)%MOD); } return 0; }