题目
城市用一个 双向连通 图表示,图中有 n 个节点,从 1 到 n 编号(包含 1 和 n)。图中的边用一个二维整数数组 edges 表示,其中每个 edges[i] = [ui, vi] 表示一条节点 ui 和节点 vi 之间的双向连通边。每组节点对由 最多一条 边连通,顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。
每个节点都有一个交通信号灯,每 change 分钟改变一次,从绿色变成红色,再由红色变成绿色,循环往复。所有信号灯都 同时 改变。你可以在 任何时候 进入某个节点,但是 只能 在节点 信号灯是绿色时 才能离开。如果信号灯是 绿色 ,你 不能 在节点等待,必须离开。
第二小的值 是 严格大于 最小值的所有值中最小的值。
- 例如,[2, 3, 4] 中第二小的值是 3 ,而 [2, 2, 4] 中第二小的值是 4 。
给你 n、edges、time 和 change ,返回从节点 1 到节点 n 需要的 第二短时间 。
注意:
- 你可以 任意次 穿过任意顶点,包括 1 和 n 。
- 你可以假设在 启程时 ,所有信号灯刚刚变成 绿色 。
示例 1:
输入:n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
输出:13
解释:
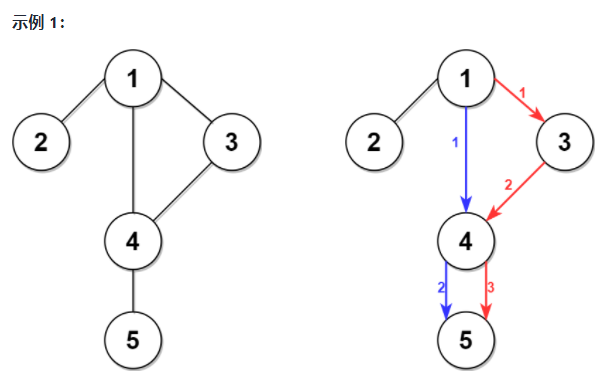
上面的左图展现了给出的城市交通图。
右图中的蓝色路径是最短时间路径。
花费的时间是:
- 从节点 1 开始,总花费时间=0
- 1 -> 4:3 分钟,总花费时间=3
- 4 -> 5:3 分钟,总花费时间=6
因此需要的最小时间是 6 分钟。右图中的红色路径是第二短时间路径。
- 从节点 1 开始,总花费时间=0
- 1 -> 3:3 分钟,总花费时间=3
- 3 -> 4:3 分钟,总花费时间=6
- 在节点 4 等待 4 分钟,总花费时间=10
- 4 -> 5:3 分钟,总花费时间=13
因此第二短时间是 13 分钟。
示例 2:

输入:n = 2, edges = [[1,2]], time = 3, change = 2
输出:11
解释:
最短时间路径是 1 -> 2 ,总花费时间 = 3 分钟
最短时间路径是 1 -> 2 -> 1 -> 2 ,总花费时间 = 11 分钟
提示:
2 <= n <= 104
n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)
edges[i].length == 2
1 <= ui, vi <= n
ui != vi
不含重复边
每个节点都可以从其他节点直接或者间接到达
1 <= time, change <= 103
BFS
力扣上的最短路径问题基本上都可以用BFS解决。BFS的队列中我们存两个信息:
- 节点id
- 到当前节点的时间
这里有两个问题需要处理:
- 红绿灯等待问题
- 找的不是最短路;而是第二短的路
第一个问题很好解决: 我们知道所有节点都是从绿灯开始,以同样的周期进行红绿灯的交替变换。 如果当前时间为 t, 一共经历了 t / change 次变化;则 t / change % 2 == 1 则为红灯, 否则为绿灯。如果当前为红灯,我们需要将时间向上取整到当前红灯结束再入队即可。
第二个问题就更简单了,记录多条路径即可。一般的权一样的最短路问题,BFS第一次搜索到终点,即找到了答案。这次我们求第二短的路,记录第二次搜索到的路径即可。可以用两个变量标记一下最短的两条路。因为严格最短,我们需要记录一下具体的值而不是出现次数。同样,一个路径如果经过了两次,我们也不用再把后面的路径加到队列中了。
//fast用来记录最快到达某节点的时间,second用来记录次快到达某节点的时间
//这两个变量和循环终止条件有关。如果没有这两个变量那么会出现死循环,因为可以任意穿过某个节点,会有源源不断的节点入队。
//那么终止条件是什么呢?即假设当前位置为pos,如果到达该位置最快和次快的时间都找到了,那么这个节点就没有必要再入队了。
private Map<Integer,Integer> fast=new HashMap<>();
private Map<Integer,Integer> second=new HashMap<>();
public int secondMinimum(int n, int[][] edges, int time, int change) {
//将Map来存储图,可以快速找到相邻节点
Map<Integer,List<Integer>> G=new HashMap<>();
Queue<List<Integer>> Q=new LinkedList<>();
for(int[] edge:edges){
if(!G.containsKey(edge[0])) G.put(edge[0],new ArrayList<Integer>());
if(!G.containsKey(edge[1])) G.put(edge[1],new ArrayList<Integer>());
G.get(edge[0]).add(edge[1]);
G.get(edge[1]).add(edge[0]);
}
Q.offer(Arrays.asList(1,0));
//用来找次快路径
int first=-1;
while(!Q.isEmpty()){
List<Integer> list=Q.poll();
int node=list.get(0);
int curTime=list.get(1);
for(int next:G.get(node)){
int targetTime=curTime+time;
if(next==n){
//第一次找到最快路径
if(first==-1) first=targetTime;
//找到次快路径
else if(first<targetTime) return targetTime;
}
//遇到红灯
if((targetTime/change)%2==1){
targetTime=(targetTime/change+1)*change;
}
//第一次找到next节点的最快路径
if(!fast.containsKey(next)){
fast.put(next,targetTime);
Q.offer(Arrays.asList(next,targetTime));
}
//第一次找到next节点的次快路径
else if(!second.containsKey(next)&&fast.get(next)<targetTime){
second.put(next,targetTime);
Q.offer(Arrays.asList(next,targetTime));
}
}
}
return -1;
}
参考:https://leetcode-cn.com/problems/second-minimum-time-to-reach-destination/solution/wei-rao-li-lun-bfsji-lu-dao-di-er-duan-d-z67m/
原题链接:https://leetcode-cn.com/problems/second-minimum-time-to-reach-destination