题目
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,找出 这个重复的数 。
示例 1:
输入:nums = [1,3,4,2,2]
输出:2
示例 2:
输入:nums = [3,1,3,4,2]
输出:3
示例 3:
输入:nums = [1,1]
输出:1
示例 4:
输入:nums = [1,1,2]
输出:1
提示:
2 <= n <= 3 * 104
nums.length == n + 1
1 <= nums[i] <= n
nums 中 只有一个整数 出现 两次或多次 ,其余整数均只出现 一次
进阶:
如何证明 nums 中至少存在一个重复的数字?
你可以在不修改数组 nums 的情况下解决这个问题吗?
你可以只用常量级 O(1) 的额外空间解决这个问题吗?
你可以设计一个时间复杂度小于 O(n2) 的解决方案吗?
方法一:位运算
public int findDuplicate(int[] nums) {
//数组元素值在1-n-1之间
int res=0,n=nums.length,digit,cnt1,cnt2;
for(int i=0;i<32;++i){
digit=1<<i,cnt1=0,cnt2=0;
for(int k=0;k<n;++k){
//1-n-1所有数和digit进行与操作
if((k&digit)>0) cnt1++;
//nums数组所有元素和digit进行与操作
if((nums[k]&digit)>0) cnt2++;
}
//只用考虑重复的数的二进制形式哪一位是1
if(cnt2>cnt1) res+=digit;
}
return res;
}
方法二:二分法
public int findDuplicate(int[] nums) {
int n=nums.length-1,left=1,right=n,mid,cnt;
while(left<right){
mid=(left+right)/2;
cnt=0;
//统计数组中小于等于mid的元素个数
for(int i=0;i<n+1;++i){
if(nums[i]<=mid) cnt++;
}
//如果重复数在[1,mid]范围内,则cnt必定大于mid
//因为此时[mid+1,n]范围内不存在重复数,最多只能有n-mid个数
if(cnt<=mid) left=mid+1;
else right=mid;
}
return left;
}
方法三:快慢指针
如何将数组看成链表
如果数组中没有重复的数,以数组 [1,3,4,2]为例,我们将数组下标 n 和数 nums[n] 建立一个映射关系 f(n)f(n),
其映射关系 n->f(n)为:
0->1
1->3
2->4
3->2
我们从下标为 0 出发,根据 f(n)f(n) 计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推,直到下标超界。这样可以产生一个类似链表一样的序列。
0->1->3->2->4->null
如果数组中有重复的数,以数组 [1,3,4,2,2] 为例,我们将数组下标 n 和数 nums[n] 建立一个映射关系 f(n)f(n),
其映射关系 n->f(n) 为:
0->1
1->3
2->4
3->2
4->2
同样的,我们从下标为 0 出发,根据 f(n)f(n) 计算出一个值,以这个值为新的下标,再用这个函数计算,以此类推产生一个类似链表一样的序列。
0->1->3->2->4->2->4->2->……
这里 2->4 是一个循环,那么这个链表可以抽象为下图:
从理论上讲,数组中如果有重复的数,那么就会产生多对一的映射,这样,形成的链表就一定会有环路了,
综上
1.数组中有一个重复的整数 <==> 链表中存在环
2.找到数组中的重复整数 <==> 找到链表的环入口
如果i=nums[i]不就自己成环了吗
以{2,1,3,4}为例,有0->2, 1->1, 2->3, 3->4,得到链表0->2->3->4,可以看出:当i=nums[i]时,链表并不会包含i这个数,因为链表延伸需要下标和数组元素交替连接。而数组中又不包含0,所以从0出发可以得到最终的链表。
链表中的环
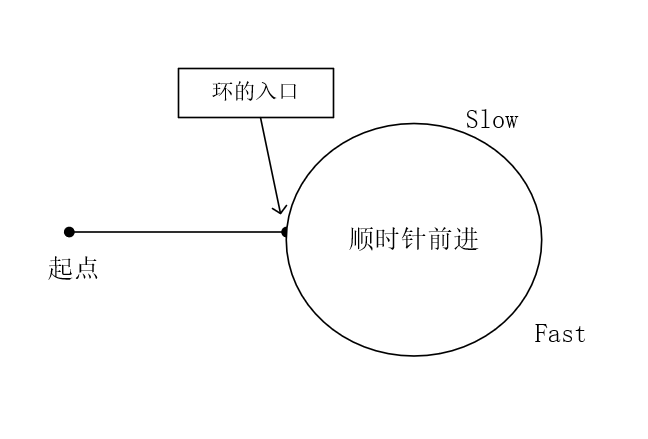
如上图,slow和fast会在环中相遇,先假设一些量:起点到环的入口长度为m,环的周长为c,在fast和slow相遇时slow走了n步。则fast走了2n步,fast比slow多走了n步,而这n步全用在了在环里循环(n%c==0)。
当fast和last相遇之后,我们设置第三个指针t,它从起点开始和slow(在fast和slow相遇处)同步前进,当t和slow相遇时,就是在环的入口处相遇,也就是重复的那个数字相遇。
为什么 t 和 slow 相遇在入口
fast 和 slow 相遇时,slow 在环中行进的距离是n-m,其中 n%c==0。这时我们再让 slow 前进 m 步——也就是在环中走了 n 步了。而 n%c==0 即 slow 在环里面走的距离是环的周长的整数倍,就回到了环的入口了,而入口就是重复的数字。
public int findDuplicate(int[] nums) {
int slow=0,fast=0,t=0;
//当slow和fast在环中相遇时结束循环
while(true){
slow=nums[slow];
fast=nums[nums[fast]];
if(slow==fast) break;
}
//找到环入口时结束循环
while(true){
slow=nums[slow];
t=nums[t];
if(slow==t) break;
}
return slow;
}
这种方法介绍了一种找到环入口的方法。之前我们做过检测链表中是否有环的问题,那么对于进阶问题————找到链表中环的入口,现在就有了一种解决思路。
参考
[1]:https://leetcode-cn.com/problems/find-the-duplicate-number/solution/287xun-zhao-zhong-fu-shu-by-kirsche/
[2]:https://leetcode-cn.com/problems/find-the-duplicate-number/solution/kuai-man-zhi-zhen-de-jie-shi-cong-damien_undoxie-d/
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/find-the-duplicate-number
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。