题目
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:

输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
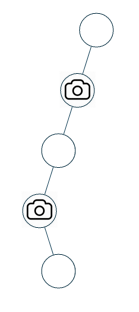
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
分析
这道题本质上是Vertex cover(顶点覆盖)问题。对于一般的无向图,Vertex cover 是一个 NPC 问题。但是对于 Tree,存在线性时间的贪心算法解决此问题。
我们在处理该问题过程中,每个二叉树节点的状态可能有以下三种:
状态0:节点没有被监控
状态1:节点被监控了但是节点上并没有摄像头
状态2:节点被监控了同时节点上安装了摄像头
我们自底向上地解决此问题,在解决过程中,先保证每个节点的所有子节点全被监控,再返回到父节点。比起把摄像头安装在0状态节点,更好地做法是把摄像头安装在0状态节点的父节点,后者监控的节点数量一定大于等于前者(自底向上搜索的情况下)。显然,我们首先遇到的0状态节点就是最底层的叶节点。
为什么自底向上搜索?自底向上即由左右孩子节点的状态判断父节点的状态。如果自上而下即由父节点的状态判断左右孩子的状态,那么问题来了,左右孩子无法获取父节点的状态。
对于一个节点,我们首先递归得到左子节点状态left和右子节点的状态right。若left等于0或right等于0,说明该节点一定要安装摄像头,摄像头数量+1后,向上返回2;否则,若left和 right 都等于1,说明该节点在状态0,我们只需把摄像头装在它的父节点,向上返回0即可;否则,说明子节点中存在摄像头,该节点已经被监控,我们向上返回1。
如果左右孩子存在至少有一个不存在怎么办?我们默认空节点的的状态为1,空节点的效果和状态为1的节点作用是一样的。最后,要注意若根节点在0状态,最终的摄像头数量需要 +1。
代码
class Solution {
private int res=0;
public int helper(TreeNode node){
if(node==null) return 1;
int l=helper(node.left),r=helper(node.right);
if(l==0||r==0) {
res++;
return 2;
}
else if(l==2||r==2) return 1;
else return 0;
}
public int minCameraCover(TreeNode root) {
if(helper(root)==0) res++;
return res;
}
}
原题链接:https://leetcode-cn.com/problems/binary-tree-cameras
参考:https://zhuanlan.zhihu.com/p/65035022