算法简介
Dijkstra算法用于解决单源最短路径问题,它根据贪心算法,按最短路径长度递增的次序产生最短路径。
基本思想
1.算法
将图的顶点集划分为两个集合S和V-S,集合S存放已经确定最短路径的终点集合。Dijkstra算法重复从节点集合V-S中选择最短路径估计最小的节点u,将u加入到集合S,然后对所有从u出发的边进行松弛操作。
(1)初始化dis[i],dis[i]表示源节点v[0]到v[i]的最短距离。
(2)选择V-S中最小的dis[j],此时的dis[j]已经是真正的v[0]到v[j]的最短距离,dis[j]=min{dis[i]|v[i]∈V−S},并将v[j]加入S。
(3)更新V-S。如果dis[j]+w[j][k]<dis[k],则dis[k]=dis[j]+w[j][k],其中v[k]∈V−S。
(4)重复(2)(3) n-1次至V-S为空。这样求得从v[0]到图上其余各顶点的最短路径是依路径长度递增的序列。
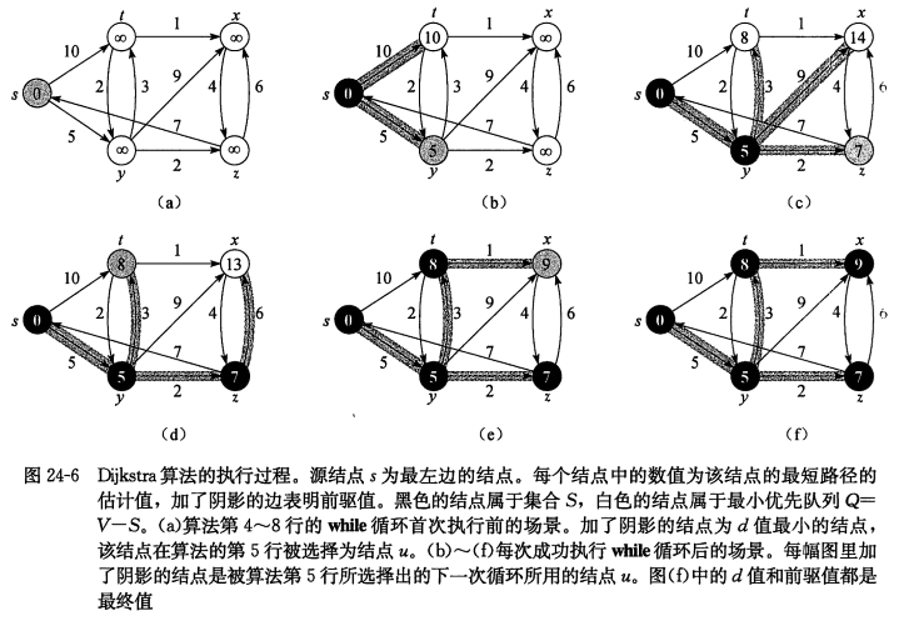
2.贪心
该算法采用了贪心的思想,每次都查找剩余节点(即V-S中的节点)中与源点距离最近的点。那么问题来了,为什么剩余节点中距离最小的节点就一定满足路径最短呢?假设这个点目前不满足路径最短,记它为vy,则剩余节点中存在中间节点vx,且路径(v0,...,vx,vy)使得vy到源点的距离更短。但是这样存在一个问题,vx到源点的距离会更短,与vy距离源点最近的前提矛盾,因此剩余节点中距离最小的节点就一定满足路径最短。
也就是说,剩余节点中其它节点满不满足路径最短不确定,但距离最小的那个点一定满足,这也是这里使用贪心算法的原因。
注意:如果求得一条vi到vj的最短路径(vi,...,vk,vj),vk是vj前面的一个顶点,那么(vi,...,vk)也必定是vi到vk的最短路径,且该路径上的顶点均满足距离源点路径最短。又因为Dijkstra算法按最短路径长度递增的次序产生最短路径,因此该路径上的顶点均在集合S中。
Dijkstra算法不能解决带有负权边的最短路径问题
原因简单来说就是如果存在负权边,就无法正确进行松弛操作。Dijkstra算法是基于贪心策略,每次都找一个距源点最近的点,然后将该距离定为这个点到源点的最短路径;但如果存在负权边,那么直接得到的最短路不一定是最短路径,因为可能先通过并不是距源点最近的一个次优点,再通过一个负权边,使得路径之和更小,这样就出现了错误。如下:
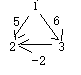
1——>2权值为5,1——>3权值为6,3——>2权值为-2,求1到2的最短路径时,Dijkstra就会选择权为5的1——>2,但实际上1——>3——>2才是最优的结果。
代码
dis[]:到源点的距离。
path[]:记录前驱节点,即w[i]表示最短路径上顶点i的前一个顶点。
vis[]:为true表示该顶点已加入S。
w[][]:表示边长。
void dijkstra(int v,int&*dis,int**w,int&*vis,int&*path){//v为源点
for(int i=0;i<n;i++){
dis[i] = w[v][i];
vis[i]=0;
if(w[v][i]<INF) path[i]=v;
else path[i]=-1;
}
vis[v]=1;//标记源点,表示v加入S
path[v]=-1;
for(int i = 1; i < n; i++){
//查找最近点,k表示该点的序号
int min = INF,k = 0;
for(int j = 0; j < n; j++)
if(!vis[j] && dis[j] < min){
min = dis[j];
k = j;
}
vis[k] = 1;//标记查找到的最近点
//更新dis[]
for(int j = 0; j < n; j++)
if(!vis[j] && min+w[k][j] < dis[j]){
dis[j] = min+w[k][j];
path[j]=k;
}
}
}
复杂度O(n^2)。
外层循环:重复执行n-1次,每次把一个最短路径的点加入S中。
内层循环:确定一个最短路径的点并更新dis数组。