二叉树是最常见最重要的数据结构之一,它的定义如下:
二叉树(binary tree)是有限多个节点的集合,这个结合或者是空集,或者由一个根节点和两颗互不相交的、分别称为左子树和右子树的二叉树组成。
二叉树最基本的操作是遍历:一般约定遍历时左节点优先于右节点,这样根据根节点的遍历顺序可分为三种遍历操作:前序-先遍历根节点,再处理左右节点;中序-先遍历左节点,然后处理根节点,最后处理右节点;后序-先遍历左右节点,然后处理根节点。
从上边二叉树定义可以看出:二叉树使用了递归的概念描述。所以,二叉树的很多操作都可以很方便的通过递归来实现,当中当然包裹遍历操作。实际上,三种遍历操作的递归实现,是二叉树其他大多数操作实现的基础:绝大多数其他操作都可以在三种遍历中的一种的基础上变化而来。
二叉树通常有两种存储方式:顺序存储和链式存储。本文代码基于链式存储方式实现,链式存储节点定义如下:
typedef struct node *tree_pointer; typedef struct node { //为了简化,节点数据用整型 int data; //指向当前节点左儿子和右儿子的指针 tree_pointer left_child, right_child; };
给出的节点定义中只有指向当前节点的左儿子和右儿子的指针,如果需要方便的知道当前的节点的父节点,可以在定义中增加指向父节点的指针: tree_pointer parent;
有了节点的定义,就可以编写二叉树的遍历函数,我们先给出递归中序遍历函数:
1 void inorder(tree_pointer ptr) 2 { 3 if (ptr) { 4 inorder(ptr->left_child); 5 printf(" %d", ptr->data); 6 inorder(ptr->right_child); 7 } 8 }
函数本身非常简洁,下面我们以图示的二叉树解释函数的遍历过程:
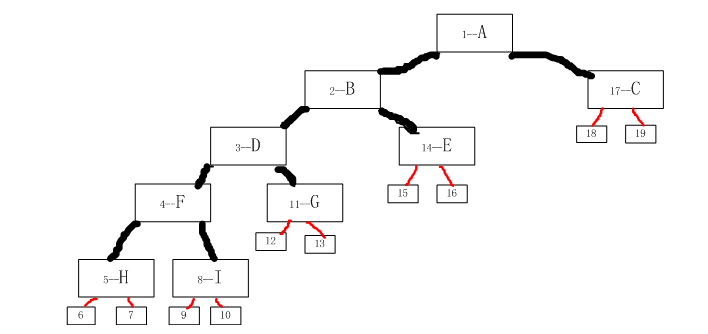
如上图所示,这颗二叉树有九个节点:ABCDEFGHI,红线连接的“节点”表示叶子节点的“左右儿子”(实际上叶子节点没有左右儿子,这里便于描述,假设存在这些NULL节点)
根据中序遍历的定义,我们可以得到这颗二叉树的中序遍历结果为:HFIDGBEAC.
把这颗二叉树的root节点指针作为参数传递给inorder函数,则函数的执行过程如下:
调用函数: inorder(root);
(下面步骤号为调用inorder函数的顺序次数)
1. 第一次调用inorder,ptr指向A,函数进入if结构,执行第四行代码,第二次调用inorder,参数为A的左儿子B;
2. ptr->B,进入if,执行line4,第三次调用inorder: inorder(B->left_child);
3. ptr->D,进入if,line4,第四次调用:inorder(D->l_c);
4. ptr->F, if, line4: inorder(F->l_c);
5. ptr->H, if, line4: inorder(H->lc);
6. ptr->NULL, 没有进入if, return;
5. 执行line5,printf(H),执行line6: inorder(H->rc);
7. ptr->NULL, 没有进入if, return回 5 ,5已经执行完毕,return 回4;
4. line5,printf(F),line6: inorder(F->rc);
8. ptr->I, if, line4: inorder(I->lc);
9. ptr->NULL, return-8;
8. line5, printf(I), line6: inorder(I->rc);
10. ptr->NULL, return-8, 8 完成,return-4, 4完成, return-3;
3. line5:printf(D), line6: inorder(D->rc);
11. ptr->G, line4: inorder(G->lc);
12. ptr->NULL, return-11;
11. line5: printf(G), line6: inorder(G->rc);
13. ptr->NULL, return-11, 11完, return-3, 3完,return-2;
2. line5:printf(B), line6:inorder(B->rc);
14. ptr->E, line4: inorder(E->lc);
15. ptr->NULL, return-14;
14. line5: printf(E), line6: inorder(E->rc);
16. ptr->NULL, return-14, 14 finished, return-2, 2 finished, return 1;
1. line5: printf(A), line6: inorder(A->rc);
17. ptr->C, line4: inorder(C->lc) ;
18. ptr->NULL, return-17;
17. line5: printf(C); line6: inorder(C->rc);
19. ptr->NULL, return-17, 17 finished, return 1, 1 finished ,return 回调用函数
完成。
上面的步骤手动描述了递归中序遍历的执行过程,其中暗含了递归调用的入栈出栈过程。
前序和后序的递归遍历与中序类似,代码实现如下:
//前序遍历 void preorder(tree_pointer ptr) { if (ptr) { printf(" %d", ptr->data); preorder(ptr->left_child); preorder(ptr->right_child); } } //后序遍历 void postorder(tree_pointer ptr) { if (ptr) { postorder(ptr->left_child); postorder(ptr->right_child); printf(" %d", ptr->data); } }
函数的执行过程也与中序基本一样,不再描述。
(在下一篇文章中将给出这些遍历函数的完整测试代码)