dp_train_f

Vasya And The Mushrooms

题目大意：有2n个格子，分成上下两行，每行n个，每个格子有蘑菇每秒的生长值（rate），小姑娘从左上角出发（time=0），每秒必须移动，而且只能移动到相邻的格子（共享一条边），每个格子只能经过一次，一旦到达格子即获得蘑菇当前时间的总量（rate*time），终点不定，求最大的蘑菇采摘量。

题解：很早就想补这题，一直没去，刚好最近开了dp专题，就想到了这一题。其实这题挺吃思维的。首先不妨把格子编号（1_{2n）（顺时针处理从左上到左下1}2n，逆时针处理从左下到左上1~2n，顺（逆）时针处理下文会提及），可以发现，由于每个格子只能经过一次，那么终点其实只有n个，因为奇数列只能是下面一行作为终点，偶数列只能是上面一行作为终点。这样一来可以发现，其实走法已经限定了，不管终点在奇数列还是偶数列（设为第i列），走法都是先从起点走↓→↑→（设为k）的整数倍再加上一部分（不妨设为ans[0][i] = a*k+b*part_k），然后从终点上（下面）面的格子开始走一个顺（逆）时针后（ans[1][i]），到达终点。最后枚举终点，计算答案，取最值（max { ans[0][i]+ans[1][i] | i E [1,n] }）即可。

实现技巧：我们发现↓→↑→走法很好统计，当算到第i列时，判断奇偶，即为ans[0][i] = ans[0][i-1]+c*a[0][i]+d*b[0][i]（c、d为步数，根据i的奇偶很好推出）。麻烦就在右边的顺时针和逆时针怎么推，这个也是我卡了很久的地方，这个真的需要一定的观察我觉得。因为是顺（逆）时针，所以可以把最大的顺（逆）时针的答案预处理出来（sum[0][i]表示顺时针到第i个格子的答案总和，sum[1][i]即为逆时针），然后观察当起点在第i列时，答案的性质，会发现和这个最大顺（逆）时针有个(i-1)*suf[i]（suf[i]表示从第i列到第n列的上下两行数值总和）的差值（例如第二张图，终点在第三列顺时针答案为456789，是最大顺时针234567，加上后面三列总和的两(i-1)倍），而显然这个差值是可以预处理出来的，那么这题也就解决了。

下面上图
△为答案所在位置，clock_max即为顺时针最大圈（第一个图）

---

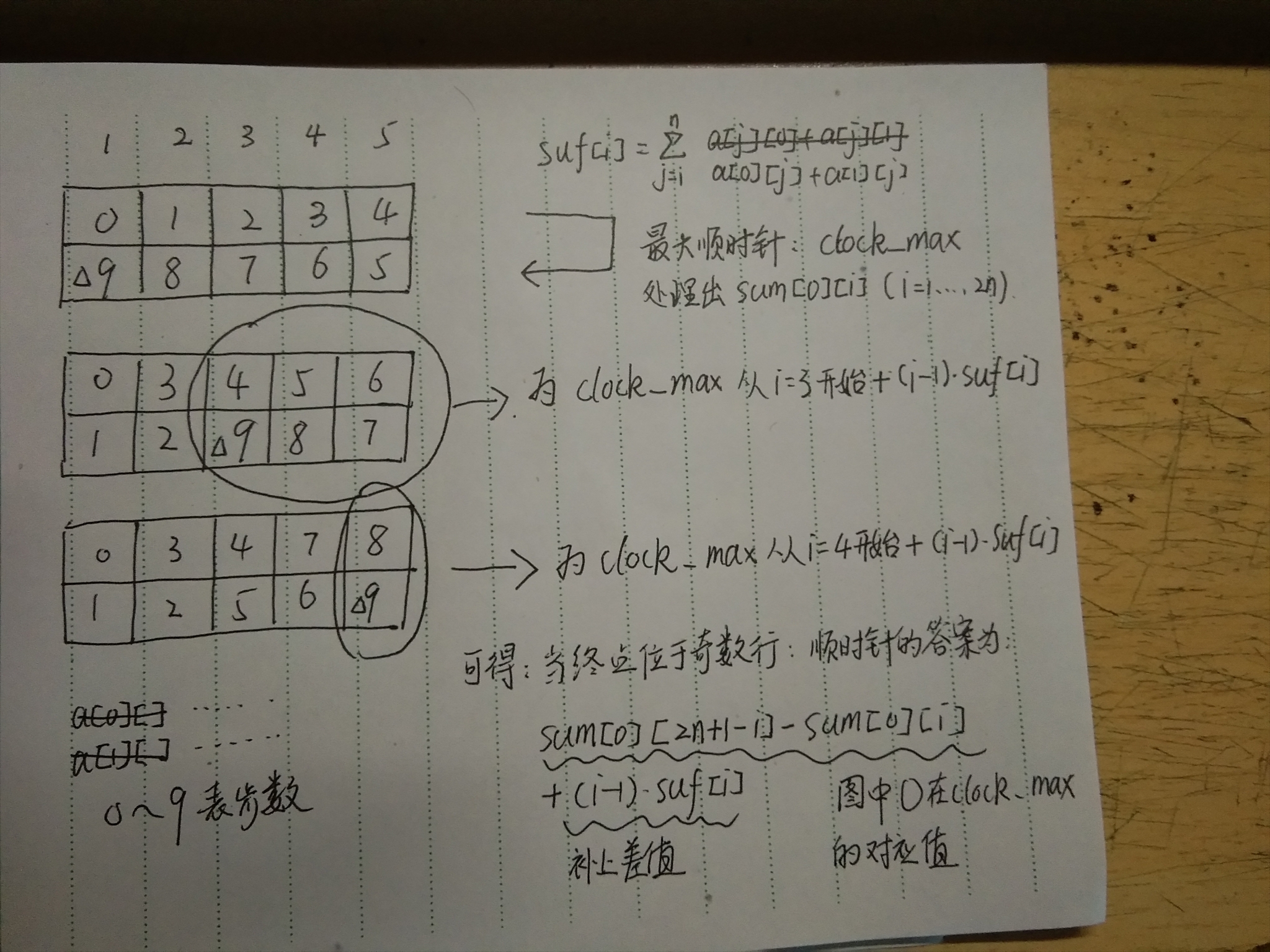
sum[0][i]表示最大顺时针到第i格（i E [1,2n]，顺时针编号），sum[1][i]则为逆时针。
ans[0][i]表示终点在第i列，左边↓→↑→走法答案，ans[1][i]表示从终点上（下面）面一格开始走顺（逆）时针到达终点的答案。
PS：这篇博客个人感觉绝对通俗易懂。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define de(x) cout << #x << " = " << x << endl
#define clr(a,b) memset(a,b,sizeof(a))
using namespace std;

typedef long long ll;
const int N = 3e5 + 16;
ll a[2][N];
ll spr[N];
ll sum[2][2*N];
ll ans[2][N];

int main()
{
	int n;
	scanf("%d", &n);
	for ( int i = 1; i <= n; i ++ )
		scanf("%I64d", &a[0][i]);
	for ( int i = 1; i <= n; i ++ )
		scanf("%I64d", &a[1][i]);
	
	clr(spr,0);
	clr(sum,0);
	clr(ans,0);
	int e = 2*n + 1;
	for ( int i = n; i >= 1; i -- )
		spr[i] = spr[i+1] + a[0][i]+a[1][i];
		
	//sum[0][]clock sum[1][]co-clock
	for ( int i = 1; i <= n; i ++ )
		sum[0][i] = sum[0][i-1] + (i-1)*a[0][i], sum[1][i] = sum[1][i-1] + (i-1)*a[1][i];
	for ( int i = n; i >= 1; i -- )
		sum[0][e-i] = sum[0][e-i-1] + a[1][i]*(e-i-1), sum[1][e-i] = sum[1][e-i-1] + a[0][i]*(e-i-1);
		
	for ( int i = 1; i <= n; i ++ )
	{
		if ( i & 1 )
		{
			ans[1][i] = sum[0][e-i] - sum[0][i-1] + (i-1)*spr[i];
			ans[0][i] = ans[0][i-1] + (2*i-3)*a[0][i-1] + (2*i-4)*a[1][i-1];
		}
		else
		{
			ans[1][i] = sum[1][e-i] - sum[1][i-1] + (i-1)*spr[i];
			ans[0][i] = ans[0][i-1] + (2*i-3)*a[1][i-1] + (2*i-4)*a[0][i-1];
		}
	}
	
	ll mx = 0;
	for ( int i = 1; i <= n; i ++ )
		mx = max( mx, ans[0][i]+ans[1][i] );
	
	printf("%I64d
", mx);
	return 0;
}