Graph_Master(连通分量_G_Trajan+Thought)

Graph_Master~(连通分量)

题目大意：给出m条边（隧道，无向），每条边连接两个点（矿场）。要在这些矿场中建设救援出口，防止矿场坍塌造成人员伤亡，问最少需要几个救援出口，以及对应方案数。（假设最多塌陷一个矿场）。

题解：这个题面给的数据比较良心，画画图知道需要找割点，然后把割点去掉跑连通块。也就是说每个连通块的颜色除了割点都是一样的，因为割点还属于别的连通块。紧接着就是统计答案了：
1、如果一个连通块没有割点，那么救援点至少建两个，方案数将乘上（这个连通块大小设为totv，包括割点）totv*(totv-1)/2，即C(2，totv)。建两个是以防如果只建一个，那个点坍塌了，就困死了，因为没有割点，就相当于是独立的，只能自生自灭。
2、如果一个连通块只有一个割点，那么救援点至少建一个，方案数乘上totv。因为如果割点坍塌，可以从救援点跑，如果救援点坍塌，可以从割点跑到另外的有救援点的连通块。
3、如果一个连通块有>=2个割点，不用建救援点，不用算方案数，因为不管怎么坍塌，都可以跑到别的有救援点的连通块。
（上图比较好理解）

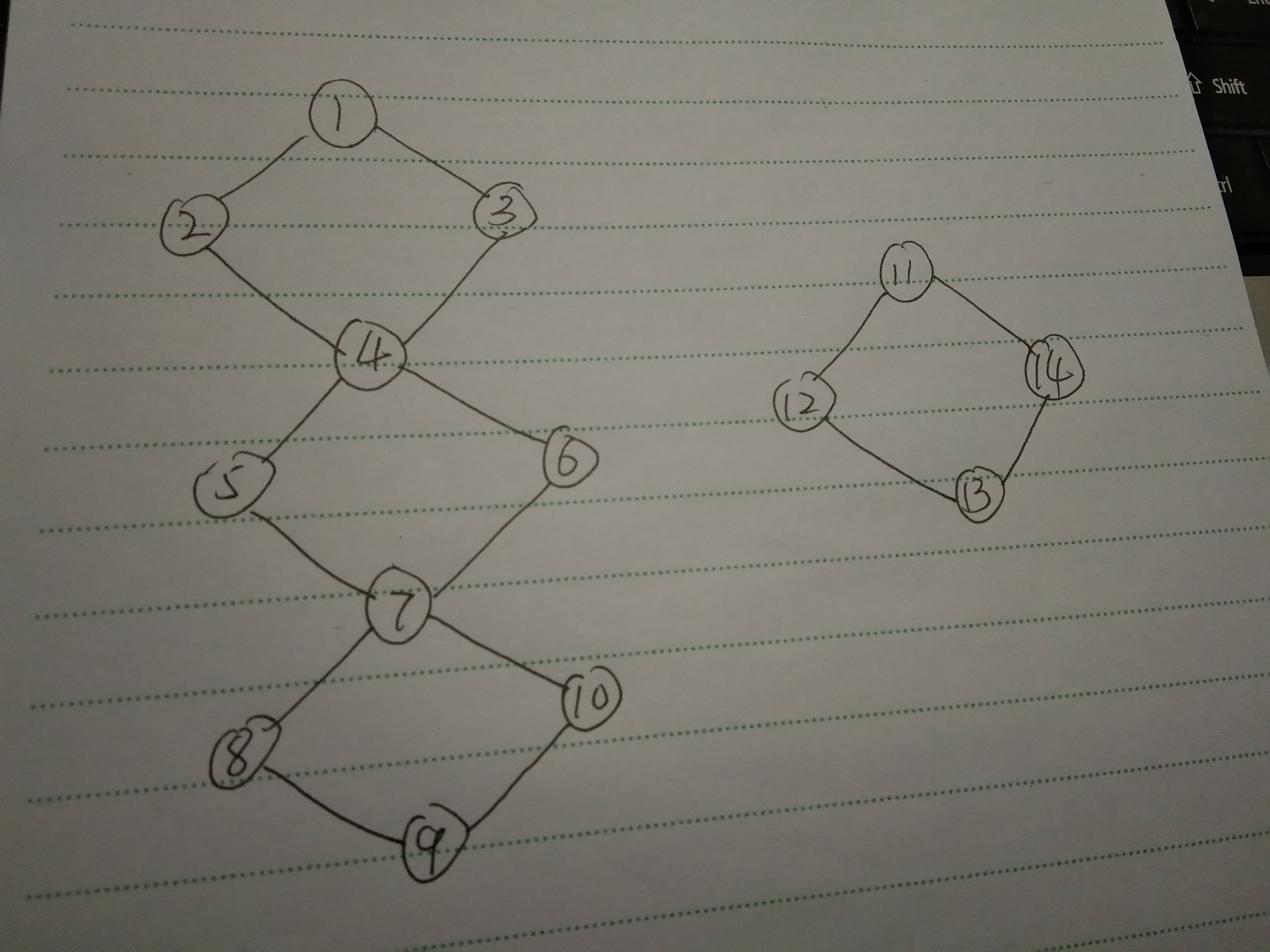
图解：1、2、3、4与7、8、9、10即为仅有一个割点（割点分别为4、7）的连通块。
4、5、6、7为有两个割点（4、7）的连通块。
11、12、13、14为没有割点的连通块（独立出来的一部分）。
有了图解每个连通块应该建几个救援点，以及如何统计方案数可以说就比较清楚了。

WA了很多发，因为没有发现used[]开成了bool，而却是用于染色，应该开成int，太粗心了。可以看到数组都远超所给范围，因为前几天给坑怕了。。

---

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cmath>
#define clr(a,b) memset((a),(b),sizeof(a))
using namespace std;

const int N = 10005;
const int M = 1e6 + 16;
typedef long long ll;

struct Edge
{
	int nxt, u, v;
};
Edge edge[M];

int ecnt, head[N];
int low[N], dfn[N];
int dep, col, cut_sum, totv;
int used[N], iscut[N];
int rt;

void init()
{
	clr(head,-1);
	clr(used,0);
	clr(iscut,0);
	clr(dfn,0);
	clr(low,0);
	ecnt = dep = col = 0;
}

void _add( int a, int b )
{
	edge[ecnt].u = a;
	edge[ecnt].v = b;
	edge[ecnt].nxt = head[a];
	head[a] = ecnt ++;
}

void tarjan( int u, int pr )
{
	low[u] = dfn[u] = ++dep;
	int son = 0;
	for ( int i = head[u]; i+1; i = edge[i].nxt )
	{
		int v = edge[i].v;
		if ( v == pr ) continue;
		if ( !dfn[v] )
		{
			son ++;
			tarjan( v, u );
			low[u] = min( low[u], low[v] );
			
			if ( low[v] >= dfn[u] )
				iscut[u] = 1;
		}
		else
			low[u] = min( low[u], dfn[v] );
	}
	if ( u == rt && son == 1 )
		iscut[u] = 0;
}

void dfs( int u )
{
	used[u] = col;
	totv ++;
	for ( int i = head[u]; i+1; i = edge[i].nxt )
	{
		int v = edge[i].v;
		if ( iscut[v] && used[v] != col )
		{
			cut_sum++;
			used[v] = col;
		}
		else if ( !used[v] )
			dfs( v );
	}
}

int main()
{
	int m;
	int cas = 1;
	while ( scanf("%d", &m), m )
	{
		int n = 0;
		init();
		for ( int i = 0; i < m; i ++ )
		{
			int u, v;
			scanf("%d%d", &u, &v);
			_add(u,v);
			_add(v,u);
			n = max( n, max(u,v) );
		}
		
		for ( int i = 1; i <= n; i ++ )
		{
			if ( !dfn[i] )
			{
				rt = i;
				tarjan( i, -1 );
			}
		}
		
		int ans1 = 0;
		ll ans2 = 1;
		for ( int i = 1; i <= n; i ++ )
		{
			if ( !used[i] && !iscut[i] )
			{
				totv = cut_sum = 0;
				col ++;
				dfs( i );
				if ( cut_sum == 0 )
				{
					ans1 += 2;
					ans2 *= 1ll*totv*(totv-1)/2;
				}
				else if ( cut_sum == 1 )
				{
					ans1 ++;
					ans2 *= 1ll*totv;
				}		
			}
		}
		
		printf("Case %d: %d %lld
", cas++, ans1, ans2);
	}
	return 0;
}