顺序表基础操作--练习

顺序表基础操作

• 存入并顺序打印数字
  //最近修改：9/21，添加插入和删除多个数字
  //9/22，修改，范围问题
• 测试图如下：
  

#include<stdio.h>
#include<stdlib.h>
#define N 20
#define OK 1
#define ERROR -1
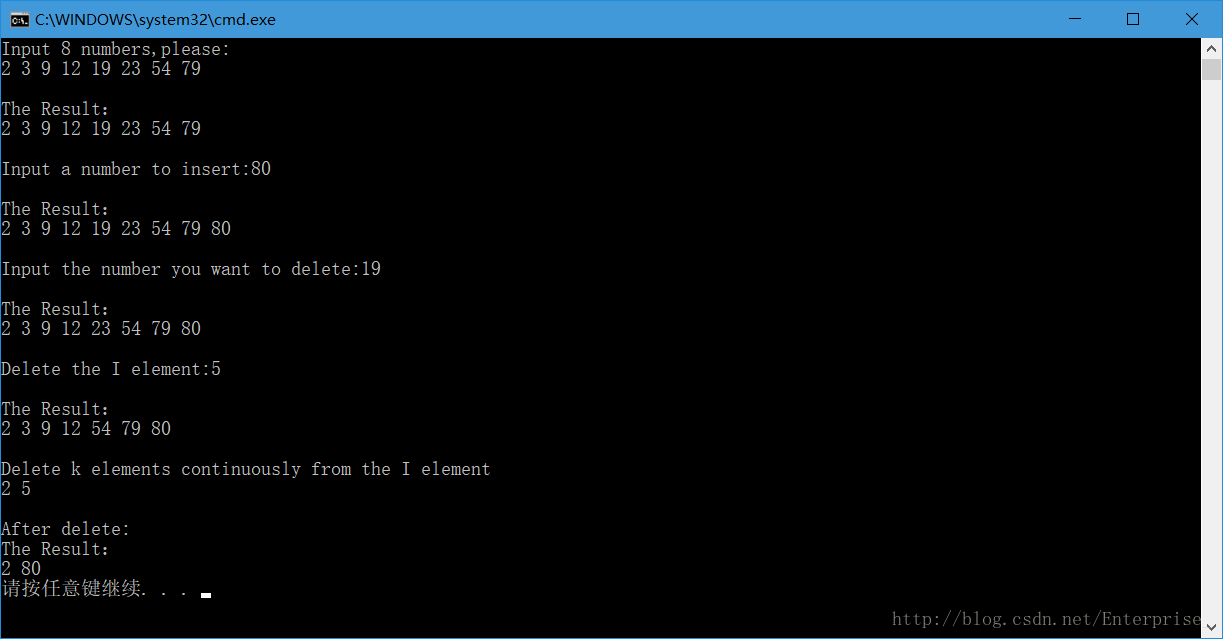
typedef struct {
    int *elem;
    int length;
    int listsize;
}SqList;

int Init(SqList *L);                                    //初始化顺序表
int ListInsert_Sq(SqList *L, int i, int e);             //在顺序表中第i个位置插入元素e
void ListPrint(SqList M);                               //顺序打印表中元素
void ListAdd_Sq(SqList *L, int e);                      //插入e之后仍然递增，前提L是顺序表
int ListDelete_X_Sq(SqList *L, int x);                  //删除值为x的元素，成功则返回1，否则返回0
int ListDelete_Sq(SqList *L, int i, int e);             //删除第i个元素
int ListDeleteFromI_to_K(SqList *L, int i, int k);      //已知一个顺序表L，从第i个元素起连续删除k个元素，这里包含第i个元素

int main(void)
{
    int i, n = 8, e, temp, k;
    SqList M;
    Init(&M);
    printf("Input %d numbers,please:
", n);
    for (i = 1; i <= n; i++)
    {
        scanf("%d", &e);
        ListInsert_Sq(&M, i, e);
    }
    ListPrint(M);
    printf("
Input a number to insert:");
    scanf("%d", &temp);
    ListAdd_Sq(&M, temp);
    ListPrint(M);
    printf("
Input the number you want to delete:");
    scanf("%d", &temp);
    ListDelete_X_Sq(&M, temp);
    ListPrint(M);
    printf("
Delete the I element:");
    scanf("%d",&temp);
    ListDelete_Sq(&M, temp, e);
    ListPrint(M);
    printf("
Delete k elements continuously from the I element
");
    scanf("%d %d", &i, &k);
    if (ListDeleteFromI_to_K(&M, i, k) != OK)
    {
        printf("out of range!
");
        exit(ERROR);
    }
    printf("
After delete:");
    ListPrint(M);
    free(M.elem);   //释放内存
    return 0;
}

int Init(SqList *L)     //初始化顺序表
{
    L->elem = (int *)malloc(N * sizeof(int));
    if (!L->elem)
        return ERROR;
    L->length = 0;
    L->listsize = N;
    return OK;
}

int ListInsert_Sq(SqList *L, int i, int e)  //在顺序表中第i个位置插入元素e
{
    int *p, *q;
    if (i < 1 || i > L->length + 1)
        return ERROR;
    q = &(L->elem[i - 1]);
    for (p = &(L->elem[L->length + 1]); p >= q; --p)
        *(p + 1) = *p;
    *q = e;
    ++L->length;
    return OK;
}

void ListPrint(SqList M)    //顺序打印表中元素
{
    int *p;
    printf("
The Result：
");
    for (p = M.elem; p <= (M.elem + M.length - 1); p++)
        printf("%d ", *p);
    printf("
");
}

void ListAdd_Sq(SqList *L, int e)  //插入e之后仍然递增，前提L是顺序表
{
    int *p, *q;
    p = L->elem;
    q = L->elem + L->length - 1;
    while (p <= q && *p<e)
        p++;
    for (; q >= p; q--)
        *(q + 1) = *q;
    *p = e;
    L->length++;
}

int ListDelete_X_Sq(SqList *L, int x) //删除值为x的元素，成功则返回1，否则返回0
{
    int *p, *q;
    p = L->elem;
    q = L->elem + L->length - 1;
    while (*p != x&&p <= q)
        p++;
    if (p > q) return ERROR;
    for (p++; p <= q; p++)
        *(p - 1) = *p;
    L->length--;
    return OK;
}

int ListDelete_Sq(SqList *L,int i,int e)
{
    int *p,*q;
    if (i < 1 || (i > L->length))   //i值不合法
        return ERROR;           
    p =&(L->elem[i - 1]);           //p为被删除元素的位置
    e = *p;                         //被删除元素的值赋给e
    q = L->elem + L->length - 1;    //表尾位置
    for (++p; p <= q; ++p)          //元素左移
        *(p - 1) = *p;      
    --L->length;                    //表长减1
    return OK;
}

int ListDeleteFromI_to_K(SqList *L, int i, int k)//已知一个顺序表L，从第i个元素起删除k个元素，这里包含第i个元素
{
    int *p, *q;
    if (i<1 || k> L->length - i + 1 || k<1)
        return ERROR;
    p = &L->elem[i - 2];
    q = L->elem + L->length - 1;
    for (p++; p<q; p++)
        *p = *(p + k);
    L->length = L->length - k;
    return OK;
}