并查集(union-find sets)

一.并查集及其优化
- 并查集：由若干不相交集合组成，是一种简单但是很好用的数据结构，拥有优越的时空复杂性，一般用于处理一些不相交集合的查询和合并问题。
- 三种操作：
1.Make_Set(x) 初始化操作，初始化的时候，每个结点各自为一个集合，这个时候father[i]=i,即此时这个结点就是这个集合的根结点，也就是它本身。
2.Find_Set(x) 查找操作，其具体功能就是找到x这个元素所在集合的根结点。可以用来判断两个结点是否在同一个集合，如果根结点不同自然就不再同一个集合中。
3.Union(x,y) 合并操作，将连个元素合并到同一个集合当中，在合并之前，一般利用Find_Set()来判断是否在同一个集合当中。

如图为合并操作：

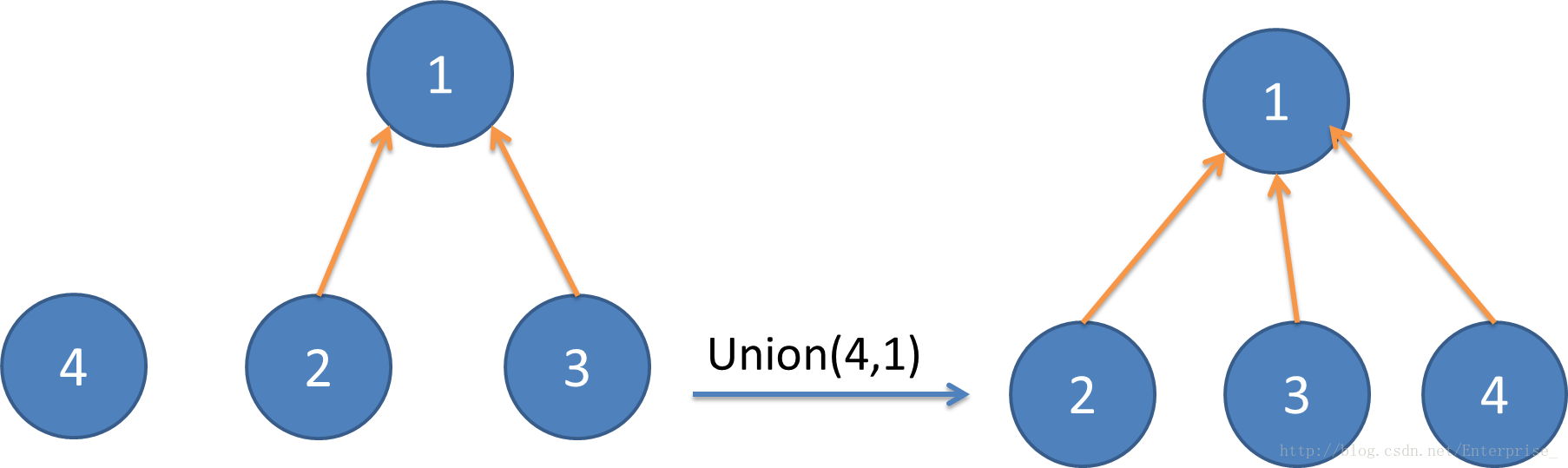
• 并查集的优化方法（改进时间的启发式策略）

  • 1 路径压缩（Path Compression）是一种在每次使用“ 查找”（Find_Set）时压扁树结构的方法。在查找过程中将查找路径上所有结点都指向根结点，把所有访问过的结点直接链接到根，这样可以减少将来的查找时间。可以想象，如果树比较极端，退化成一条链了，那么在最坏的时候每次查询都达到了O(n),而路径压缩就可以提高效率。
    而且，路径压缩并不改变任何节点的秩，但是会改变子树的高度.

    具体如下图所示:
    

  • 2 按秩合并(Union by rank)其思想是把包含较少节点的树的根指向包含较多节点的树的根，将较短的树连接到较高的树的根部，这样可以降低树的高度。
    这里需要使用一个Rank来记录秩的变化，每一个结点都有对应的一个Rank,,最初的集合中只有一个根结点，以及一个为0的Rank(秩)。在这里秩只是表示结点高度的一个上界。秩用来代替了高度或者深度，这是因为路径压缩会改变树的高度，所以不记录子树的高度的准确值，而是采用上界这样一个估计值来表示。
    具体如下图所示:
    

• 代码实现：

#define MAX 5000
int n, m, Father[MAX], Rank[MAX];
void Make_Set(int x)
{
    Father[x] = x;
    Rank[x] = 0;
}
int Find_Set(int x) 
{   //递归写法，数据量比较少的时候可以写
    return Father[x] == x ? x : Father[x] = Find_Set(Father[x]); 
}
int Find_Set(int x)
{
    //递归写法，数据极端容易RE，可能栈溢出。默认堆栈的大小为8192KB.
    if (x != Father[x])
        Father[x] = Find_Set(Father[x]);
    return Father[x];
}
int Find_Set(int x)  //非递归写法,适合数据量比较大的时候
{
    int p = x, temp;
    while (Father[p] != p) p = Father[p];
    while (x != p)
    {
        temp = Father[x];
        Father[x] = p;
        x = temp;
    }
    return x;
}
void Union(int x, int y)   //按秩合并
{
    x = Find_Set(x);
    y = Find_Set(y);
    if (x == y) return;
    if (Rank[x] > Rank[y])  /*如果x的Rank比较高，就把x作为y的父节点*/
    {
        father[y] = x;
        Rank[x] += Rank[y];
    }
    else
    {
        father[x] = y;    
        if (Rank[x] == Rank[y])
        {
            Rank[y]++;   
        }
    }
}

• 时间复杂度的考虑
  有几种情况，即是否使用路径压缩(Path Compression)和按秩合并(Union by rank)的四种情况，如果不使用优化手段，树可以无限制的增长，这样查找和合并的时间就是O(n).
  只是使用路径压缩(Path Compression)的话，最坏的时间就是
  
  只是使用按秩合并(Union by rank)的话，时间可以达到O(mlog n),其中n为结点数目。
  当同时使用的时候。可以确保每个操作分摊下来的时间是O(α(n))，这是最优的，
  这个α(n)是 inverse Ackermann function(逆阿克曼函数),当我们现在宇宙中的任何n值，可以得知α(n)<5，所以并查集运算基本恒定。
  详细参考：维基百科
  二.并查集基本应用
  从题目开始：HDU1232 畅通工程
• 题目分析：建设最少的道路，使得所有城镇都相互交通，但不一定有直接的道路相连，只要互相间接通过道路可达即可。
• 换句话说，这里就是在求有几个不相交的集合数，更准确就是求这个无向图的连通分量个数
  AC代码如下：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstdbool>
#include<algorithm>
using namespace std;
#define MAX 1005
int Father[MAX];
void init()
{
    for (int i = 1; i < MAX; i++)
        Father[i] = i;
}
int Find_Set(int x)
{   //递归写法，数据量比较少的时候可以写
    return Father[x] == x ? x : Father[x] = Find_Set(Father[x]);
}
void Union(int x, int y)
{
    x = Find_Set(x), y = Find_Set(y);
    if (x != y)
        Father[x] = y;
}
int main(void)
{
    int m, n, t1, t2;
    while (scanf("%d", &n) != EOF)
    {
        if (n == 0)
            break;
        scanf("%d",&m);
        init();
        while (m-- > 0)
        {
            scanf("%d%d",&t1,&t2);
            Union(t1, t2);
        }
        int ans = 0;
        for (int i = 1; i <= n; i++)  
        {
            if (Father[i] == i)
                ans ++;
        }
        printf("%d
",ans - 1);
    }
}

下面是使用了按秩合并的写法:

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstdbool>
#include<algorithm>
using namespace std;
#define MAX 1005
int Father[MAX], Rank[MAX];
void init()
{
    for (int i = 1; i < MAX; i++)
        Father[i] = i;
}
int Find_Set(int x)
{   //递归写法，数据量比较少的时候可以写
    return Father[x] == x ? x : Father[x] = Find_Set(Father[x]);
}
void Union(int x, int y)   //按秩合并
{
    x = Find_Set(x);
    y = Find_Set(y);
    if (x == y) return;
    if (Rank[x] > Rank[y])  /*如果x的Rank比较高，就把x作为y的父节点*/
    {
        Father[y] = x;
        Rank[x] += Rank[y];
    }
    else
    {
        Father[x] = y;
        if (Rank[x] == Rank[y])
        {
            Rank[y]++;
        }
    }
}
int main(void)
{
    int m, n, t1, t2;
    while (scanf("%d", &n) != EOF)
    {
        if (n == 0)
            break;
        scanf("%d",&m);
        init();
        while (m-- > 0)
        {
            scanf("%d%d",&t1,&t2);
            Union(t1, t2);
        }
        int ans = 0;
        for (int i = 1; i <= n; i++)  
        {
            if (Father[i] == i)
                ans ++;
        }
        printf("%d
",ans - 1);
    }
}

三.带权并查集
- 带权并查集，是指结点存有权值信息的并查集。并查集以森林的形式存在， 而结点的权值大多是记录该结点与祖先关系的信息。
比如权值可以记录该结点到根结点的距离，也可以是相对于根节点的状态。

1.食物链（POJ1182）这道题是十分经典的关于带权并查集的题目，就是维护当前结点和根结点关系。
- 题目分析：有三种动物，存在互相吃与被吃的关系，A吃B， B吃C，C吃A。现在给定K句话，这些话中有真有假，现在需要判断其中假话的个数。

• 一种思路，通过并查集来将所有同时出现的情况都合并到一起，如果1能吃掉2，那么只有三种情况：
• 1是A，2是B
• 1是B，2是C

• 1是C，2是A
  然后把 1是A 和 2是B 的情况合并到一起，同理对于剩下两种情况 ，这样处理之后，如果之后又加入了一句话发现 2是B 和 2是A的情况在一个集合中，那么就一定判断这句话是假的了。

• 之后发现有更好的方法：这里的难点就在于不知道具体是什么动物。
  虽然不知道每个数字对应的动物，但是可以知道动物之间的关系。那么就可以把已知关系的点合并在一棵树上，然后记录每个点与根结点的关系。这里采用的规则如下：
  如果一个点和根结点的相同那么关系记为 0，
  如果一个点可以吃掉根结点那么关系记为 1，
  如果一个点可以被根结点吃掉那么关系记为 2。
  我们只要一直维护每个点与根结点的关系，这样我们就可以判断某一个描述是否与之前的描述冲突了。
  具体而言，在判断X,Y的关系的时候，找出X,Y的根结点A,B
  如果A!=B,则X,Y还没有建立联系，此时关于这两个元素的判断都可以认为是对的。之后需要合并这两个子树，具体关系如下图所示这里的式子
  
  要满足(reltion[x] + t) % 3 = (d + relation[y]) % 3，所以 t = (d + relation[y] - relation[x] + 3) % 3，满足这一个条件，既可以判断这句话正确性。
  如果A==B,说明存在关系，这个时候需要判断是否正确，通过求和取模的关系，这个是通过找规律得来， 需要写出一些情况来合理推断。

• AC代码

#include <map>
#include <iostream>
#include<cstdio>
using namespace std;
int father[500999];
int relation[500099];
void Make_Set(int n)
{
    for (int i = 1; i <= n; i++)
    {
        father[i] = i;
        relation[i] = 0;
    }
}
int Find_Set(int x)
{
    if (father[x] == x)
        return x;
    else
    {
        int t = father[x];
        father[x] = Find_Set(father[x]);
        relation[x] = (relation[t] + relation[x]) % 3;
        return father[x];
    }
}

int main()
{
    int i, flag = 0, N, K, D, X, Y, A, B;
    int res;
    scanf("%d", &N);
    Make_Set(N);
    scanf("%d",&K);
    for (i = 0; i < K; i++)
    {
        scanf("%d%d%d",&D,&X,&Y); 
        if ((X > N) || (Y > N) || X == Y && D == 2)
        {
            flag++;
        }
        else
        {
            A = Find_Set(X);
            B = Find_Set(Y);
            if (A != B)
            {
                father[B] = A;
                relation[B] = (D - 1 + relation[X] - relation[Y] + 3) % 3;
            }
            else
            {
                if ((relation[Y] - relation[X] + 3) % 3 != D - 1)
                    flag++;
            }
        }
    }
    printf("%d
",flag); 
}

2.再比如这道题:POJ1703 Find them, Catch them

• 题目分析：有两个帮派，给若干条信息，根据所给信息来判断所询问的两个人是否是同一个帮派。信息包括D [a] [b]， 其中[a]和[b]是两个罪犯的标号，他们属于不同的帮派。 A[a][b],这是询问是否ab在同一个集合。
• 思路：这里明显可以使用并查集，但是给的信息是不同集合的，而并查集是保存同一个集合，所以单纯的并查集是不行了，故增加一个flag,来标记当前结点和根结点的关系，用一个并查集来维护所有的结点。在这里，我使用的规则是：如果当前结点和根结点是一个集合则标记为0，否则为1。
  这样只要一直维护每个点与根结点的关系，就可以判断某一个询问的两个人是否在同一个帮派。
• 注意：这里有一个特例，就是一共只有两个人的时候，他们是在不同帮派的。
• 关系转移为在Find_Set()的时候和上一层父亲节点的flag相加，需要查找规律得出。
• AC代码如下：

#include<iostream>
#include<cstdio>
#define MAX  100005
using namespace std;
int father[MAX], flag[MAX];
void Make_Set(int n)
{
    for (int i = 1; i <= n; i++)
    {
        father[i] = i;
        flag[i] = 0;
    }
}

int Find_Set(int x)
{
    if (father[x] == x)
        return x;
    else
    {
        int t = father[x];
        father[x] = Find_Set(father[x]);
        flag[x] = (flag[t] + flag[x]) % 2;      //状态转移,0和1分别代表是一个集合，不是一个集合的状态
        return father[x];                       //当前结点的状态等于前面两个结点的状态的叠加态
    }
}

void Union(int a, int b)
{
    int x = Find_Set(a);
    int y = Find_Set(b);
    father[x] = y;                                  
    flag[x] = (flag[b] + flag[a] + 1 ) % 2;   //状态转移,0和1分别代表是一个集合，不是一个集合的状态
}

int main(void)
{
    char check;
    int T, M, N, mem1, mem2, t1, t2;
    scanf("%d",&T);
    while (T-- > 0)
    {
        scanf("%d %d",&N,&M);
        Make_Set(N);
        while(M-->0)
        {
            getchar();//之前有个换行需要接受，否则WA
            scanf("%c %d %d",&check, &mem1, &mem2);
            if (N == 2 && check=='A')  //特殊样例
            {
                printf("In different gangs.
");
            }
            else if (check == 'D')
            {
                Union(mem1, mem2);
            }
            else
            {
                t1 = Find_Set(mem1);
                t2 = Find_Set(mem2);
                if (t1 != t2)
                {
                    printf("Not sure yet.
");
                }
                if (t1 == t2)
                {
                    if(flag[mem1] != flag[mem2])
                        printf("In different gangs.
");
                    else
                        printf("In the same gang.
");
                }
            }
        }
    } 
    return 0;
}

3.POJ2492 A Bug’s Life

• 题目分析：假设所有bug只能异性之间交配，出现同性则错误
• 思路：同样使用带权并查集，用flag表示当前结点和根结点的相对关系，两个虫子如果是异性，则一个为0，一个为1，用第一个关系为依据，后面的虫子逐渐更新和根结点的关系，如果发现某两个虫子的flag相同，则为错误信息。
• 合并x,y的关系式为：
  flag[b] = (flag[x] - flag[y] + 1) % 2，
  flag[b] = (flag[x] - flag[y] + 1) % 2,
  其中，a是x的根结点，b是y的根结点。
• AC代码如下：

#include<iostream>
#include<cstdio>
#define MAX  100005
using namespace std;
int father[MAX], flag[MAX], Rank[MAX];
void Make_Set(int n)
{
    for (int i = 1; i <= n; i++)
    {
        father[i] = i;
        flag[i] = 0;
        Rank[i] = 0;
    }
}

int Find_Set(int x)
{
    if (father[x] == x)
        return x;
    else
    {
        int t = father[x];
        father[x] = Find_Set(father[x]);
        flag[x] = (flag[t] + flag[x]) % 2;      //状态转移,0和1分别代表是一个集合，不是一个集合的状态
        return father[x];                       //当前结点的状态等于前面两个结点的状态的叠加态
    }
}

void Union(int x, int y)
{
    int a = Find_Set(x);
    int b = Find_Set(y);
    if (a == b) return;
    if (Rank[a] > Rank[b])  //按秩合并
    {
        father[b] = a; 
        Rank[a] += Rank[b];
        flag[b] = (flag[x] - flag[y] + 1) % 2;
    }
    else
    {
        if (Rank[a] == Rank[b])
        {
            Rank[b]++;
        }
        father[a] = b;
        flag[a] = (flag[y] - flag[x] + 1) % 2;
    }
}
int main(void)
{
    int n, m, T, gg, mm, ans;
    scanf("%d",&T);
    for(int i=1;i<=T;i++)
    {
        ans = 0;
        scanf("%d %d",&n,&m);
        Make_Set(n);
        while (m-- > 0)
        {
            scanf("%d %d",&gg,&mm);
            Union(gg, mm);
            if (flag[gg] == flag[mm] && father[gg] == father[mm])
                ans = 1;
        }
        printf("Scenario #%d:
",i);
        if (ans == 1)
            printf("Suspicious bugs found!
");
        else
            printf("No suspicious bugs found!
");
            putchar(10);
    }
    return 0;
}

当然还有其他的应用，比如LCA(最近公共祖先问题，以及实现Kruskar算法求最小生成树，还在学习ing.
参考文章来源：http://www.ahathinking.com/archives/10.html