【前缀和与差分】
1.前缀和求区间和
sum[] for(int i = 1; i <= n; i++) { sum[i] = sum[i - 1] + a[i]; } while(q--) { int l, r; scanf("%d %d", &l, &r); printf("%d ", sum[r] - sum[l - 1]); }
2.差分维护区间修改求值
差分可以将【区间(或多次单点)修改,单点查询】改为【单点修改,区间查询】。
差分是前缀和的逆运算,用于记录修改的状态,不能插入元素和删除。


b[] for(int i = 1; i <= n; i++) { b[i] = a[i] - a[i - 1]; } while(q--) { int l, r, x; scanf("%d %d %d", &l, &r, &x); b[l] += x, b[r + 1] -= x; } for(int i = 1; i <= n; i++) { b[i] += b[i - 1]; }
3.分块的概念与运用
【例题1】

SOLUTION1
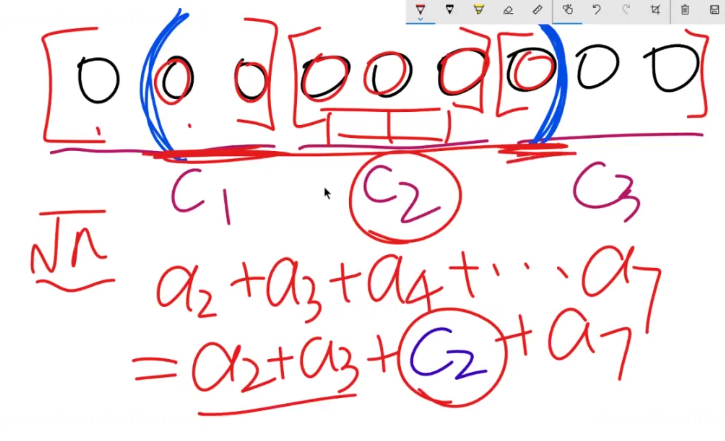
将查询区间分成中间整块+零散两边,此时两部分都在根号n范围。
简单来说就是大部分分块,小部分暴力。
分块时:块的大小为根号n,建立每个位置对应的块的编号。
修改时:直接修改值和相应块的值。(单点修改)
用getStart函数求出每分块的第一个。
注意写getEnd函数时,要写 min(n,getStart[k+1]-1)。

↑↑ getEnd(4)的正确答案应该是10。
- 为什么块数是根号n(或根号n+1)?
- 答:每段长为s,块数是n/s。查询区间最大为n/s+2s(零散块)。
- 数学方法可以求得,s最优为根号n,n/s=根号n。(如下图)

文字版理解
代码实现
c[] int size = (int)sqrt(n); int getBlock(int x) { // 1-based return (x - 1) / size + 1; } int getStart(int b) { return (b - 1) * size + 1; } int getEnd(int b) { return min(n, getStart(b + 1) - 1); } for(int i = 1; i <= n; i++) { c[getBlock(i)] += a[i]; } while(q--) { int opt; scanf("%d", &opt); if(opt == 1) { int p, x; scanf("%d %d", &p, &x); // a[p] += x a[p] += x; c[getBlock(p)] += x; } else { int l, r; scanf("%d %d", &l, &r); if(getBlock(l) == getBlock(r)) { int ans = 0; for(int i = l; i <= r; i++) { ans += a[i]; } printf("%d ", ans); } else { int ans = 0; for(int i = getBlock(l) + 1; i <= getBlock(r) - 1; i++) { ans += c[i]; } for(int i = l; i <= getEnd(getBlock(l)); i++) { ans += a[i]; } for(int i = getStart(getBlock(r)); i <= r; i++) { ans += a[i]; } printf("%d ", ans); } } }
SOLUTION2
这里不用分块的方法,是【暴力存储变化+重构数组】。

sum[] for(int i = 1; i <= n; i++) { //预处理前缀和 sum[i] = sum[i - 1] + a[i]; } vector<pair<int, int> > modify; int C = (int)sqrt(q); while(q--) { int opt; scanf("%d", &opt); if(opt == 1) { int p, x; scanf("%d %d", &p, &x); // a[p] += x modify.push_back(make_pair(p, x)); if(modify.size() > C) { //到一定长度,清空数组【暴力重构法】 for(int i = 0; i < modify.size(); i++) { a[modify[i].first] += modify[i].second; //某记录修改的位置 } for(int i = 1; i <= n; i++) { //前缀和修改 sum[i] = sum[i - 1] + a[i]; } modify.clear(); } } else { int l, r; scanf("%d %d", &l, &r); int ans = sum[r] - sum[l - 1]; for(int i = 0; i < modify.size(); i++) //等到询问时,再一起修改变化的值 if(modify[i].first >= l && modify[i].first <= r) ans += modify[i].second; printf("%d ", ans); } }
pair中:修改位置和修改值,用来记录修改。
【重构】是防止modify很大而维护的定长,C=根号n。
【例题2】

SOLUTION

区间加想到差分,转化为单点修改+区间求和,区间和想到分块。
4.二维前缀和
(1) 求二维前缀和 ---- 容斥原理
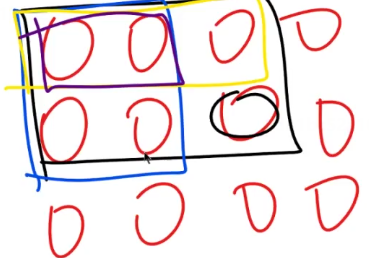
sum[][] //方法一 for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { sum[i][j] = a[i][j] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1]; } } //方法二(更优) for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { sum[i][j] = a[i][j]; } } for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { sum[i][j] += sum[i - 1][j]; } //sum[i-1][j]中没有加sum[i-1][j-1],相当于剪掉 } for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { sum[i][j] += sum[i][j - 1]; } }
(2)二维前缀和表示二维区间
下方图示为,求紫色块:
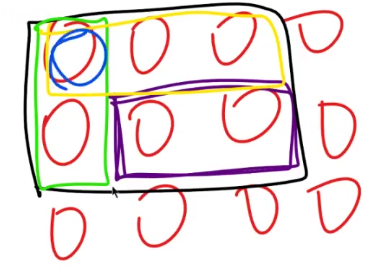
int query(int x1, int y1, int x2, int y2) { return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1]; }
【例题3】(单点修改+二维区间查询)
SOLUTION
分块·法2【暴力存储变化+重构数组】+二维前缀和。
这里的C要取根号n*m,解释如下。

vector数组记录修改,pair<a,b>为点序,c为点的价值。

sum[][] vector<pair<pair<int, int>, int> > modify; int query(int x1, int y1, int x2, int y2) { return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1]; } for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { sum[i][j] = a[i][j] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1]; } } int C = (int)sqrt(n * m); while(q--) { int opt; scanf("%d", &opt); if(opt == 1) { int x1, y1, x2, y2; scanf("%d %d %d %d", &x1, &y1, &x2, &y2); int ans = query(x1, y1, x2, y2); for(int i = 0; i < modify.size(); i++) { int curX = modify[i].first.first; int curY = modify[i].first.second; if(curX >= x1 && curX <= x2 && curY >= y1 && curY <= y2) { ans += modify[i].second; } } } else { int x, y, z; scanf("%d %d %d", &x, &y, &z); modify.push_back(make_pair(make_pair(x, y), z)); if(modify.size() > C) { for(int i = 0; i < modify.size(); i++) { int curX = modify[i].first.first; int curY = modify[i].first.second; a[curX][curY] += modify[i].second; } for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { sum[i][j] = a[i][j] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1]; } } modify.clear(); } } }
【例题4】(区间修改+二维单点查询)

SOLUTION

↑↑ 第四行应该改成a数组的修改。
图示:差分的区间修改记录(差分数组就是矩形前缀和数组)

b[][] for(int i = 1; i <= n; i++) { for(int j = 1; j <= m; j++) { b[i][j] = a[i][j] + a[i - 1][j - 1] - a[i - 1][j] - a[i][j - 1]; } }
【树状数组】知识点
1.定义
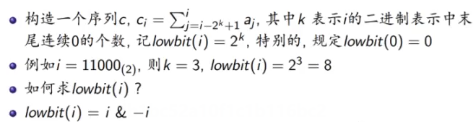
int lowbit(int x) { return x & -x; } c[] for(int i = 1; i <= n; i++) { for(int j = i - lowbit(i) + 1; j <= i; j++) { c[i] += a[j]; } } int sum(int x) { if(x < 1) return 0; int ans = c[x]; return ans + sum(x - lowbit(x)); }
2.性质


【例题5】(树状数组模板题)

SOLUTION

【例题6】(树状数组模板题)

SOLUTION


