【暖*墟】#洛谷网课1.31# 多项式与概率

多项式及相关操作

一个 R 上的关于 x 的多项式可以写作：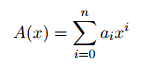

其中 ai ∈ R。x 被称为这个多项式的自由元。

多项式的次数被定义为其最高次项的次数，记为 deg A(x)。

多项式加法与乘法

卷积的概念

多项式与点值

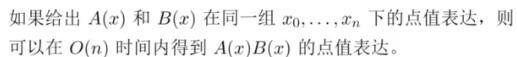
• 如何让在多项式系数和点值表达之间转换？-->考虑一组特殊的点值

       

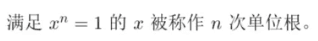
复数的加法和乘法

 

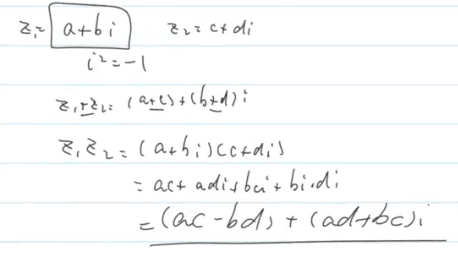
struct complex{
     double x,y;
     complex(){}
     complex(double x,double y){this->x=x,this->y=y;}
     complex friend operator +(complex n1,complex n2){return complex(n1.x+n2.x,n1.y+n2.y);}
     complex friend operator -(complex n1,complex n2){return complex(n1.x-n2.x,n1.y-n2.y);}
     complex friend operator *(complex n1,complex n2){return complex(n1.x*n2.x-n1.y*n2.y,n1.x*n2.y+n1.y*n2.x);}
};

共轭复数与复数除法

共轭复数：z=a+b*i,z_=a-b*i;

z*z_=a^2+b^2; 则：z1/z2=(z1*z2_)/(z2*z2_)=(z1*z2_)/(c^2+d^2);

单位根与本原单位根

 

由欧拉公式： ，可以推出：

在复数域上，本原单位根：（其中 exp（x）=e^x）

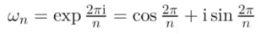
在有限域上，本原单位根和数论中的原根有关。

离散傅里叶变换（DFT）

• DFT本质上就是函数对应的点值。

单位根的一些性质

两条性质的证明过程：

（1）

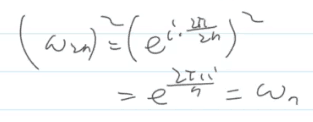
（2）

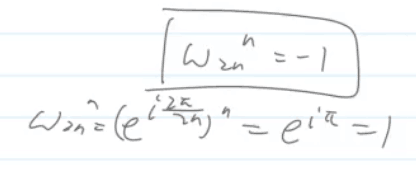
“蝴蝶操作”的过程

 

 

拆开式子，再分析一遍：

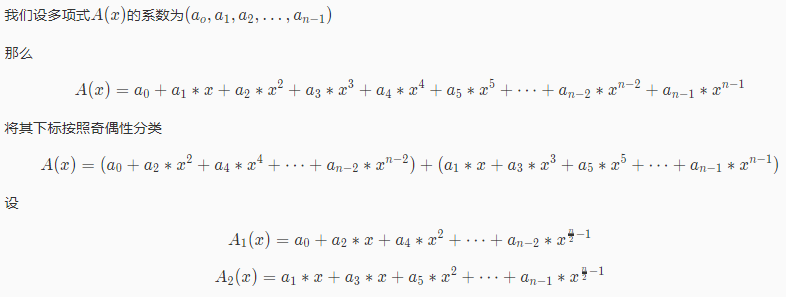
在枚举第一个式子的时候，我们可以O(1)的得到第二个式子的值，

又因为第一个式子的k在取遍[0,n/2−1]时，k+n/2​取遍了[n/2,n−1]。

那么每次都可以把问题缩小一半，用分治思想不停递归求解即可。

快速傅里叶变换（FFT）

位逆序置换 与 非递归FFT

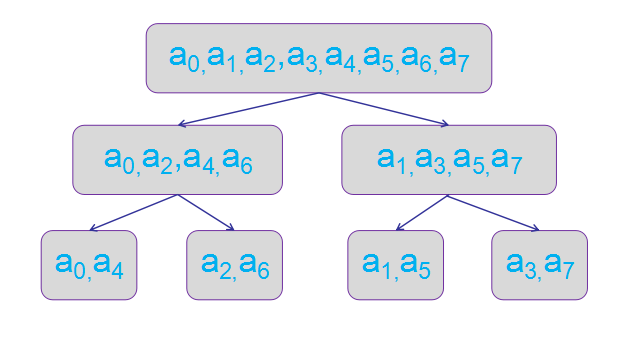
原数列数字	0	1	2	3	4	5	6	7
二进制	000	001	010	011	100	101	110	111

最底层数列数字	0	4	2	6	1	5	3	7
二进制	000	100	010	110	001	101	011	111

发现二进制表示反过来了。于是我们可以得到一个转换方法：

for(int i=0;i<len;i++) turn[i]=turn[i>>1]>>1|((i&1)<<L);

离散傅里叶变换的逆变换（IDFT）

调整求和顺序，转化成不同的式子。（k是一个独立于 i、j 的值）

 

 

FFT进行多项式乘法

假设 A(x), B (x) 是两个不超过 n 次的多项式，

那么他们的乘积 A(x)*B(x) 则可能是不超过 2n − 1 次的多项式。

因此我们一般会对 A(x), B (x) 进行长度至少 2n 的 DFT，

然后把对应的点值乘起来，再进行对应长度的 IDFT。

DFT 与 FFT 都是在 复数域 C 中进行的过程。

但往往是对整数进行操作，并且经常要对某个素数 p 取模。

考虑在模素数的时候，是否存在和单位根性质类似的元素。

实现思路：系数表示法—>点值表示法—>系数表示法。

原根的定义与性质

设 p 是素数。由费马小定理，对于任意 a 满足互质，有：

a^(p−1) ≡ 1 (mod p)

g 称为模 p 的原根，当且仅当 g0, g1, . . . , g(p−2)在模 p 意义下互不相同。

可以证明，原根总是存在的。原根的性质和本原单位根非常类似。

换句话说，在 mod p 意义下，g 可以被看做一个 p − 1 次本原单位根。

FFT具体过程及代码实现

三重循环：1.合并的序列长度 ； 2.枚举具体每一位；3.蝴蝶操作优化。

void FFT(complex *a,int typ){
    for(int i=0;i<len;i++)
        if(i<turn[i]) swap(a[i],a[turn[i]]);
    for(int l=1;l<len;l<<=1){
        wn=complex(cos(pi/l),typ*sin(pi/l));
        for(int p=0;p<len;p+=(l<<1)){
            w=complex(1,0); //a+b*i
            for(int i=p;i<p+l;i++,w=w*wn){
                tmpx=a[i],tmpy=w*a[i+l];
                a[i]=tmpx+tmpy,a[i+l]=tmpx-tmpy;
            } //↑↑用“蝴蝶操作”优化
        }
    }
}

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<cmath>
#include<map>
using namespace std;
typedef long long ll;

//【p3803】FFT求卷积模板

void reads(int &x){ //读入优化（正负整数）
    int fa=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')fa=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();}
    x*=fa; //正负号
}

const int N=(1<<21)+10;

struct complex{ //复数
    double x,y;
    complex(){} //复数的相关运算
    complex(double x,double y){this->x=x,this->y=y;}
    complex friend operator +(complex n1,complex n2)
      {return complex(n1.x+n2.x,n1.y+n2.y);}
    complex friend operator -(complex n1,complex n2)
      {return complex(n1.x-n2.x,n1.y-n2.y);}
    complex friend operator *(complex n1,complex n2)
      {return complex(n1.x*n2.x-n1.y*n2.y,n1.x*n2.y+n1.y*n2.x);}
}a[N],b[N],tmpx,tmpy,wn,w;

const double pi=3.1415926535897632;

int n,m,turn[N],len=1,L=-1;

void FFT(complex *a,int typ){
    for(int i=0;i<len;i++)
        if(i<turn[i]) swap(a[i],a[turn[i]]);
    for(int l=1;l<len;l<<=1){
        wn=complex(cos(pi/l),typ*sin(pi/l));
        for(int p=0;p<len;p+=(l<<1)){
            w=complex(1,0); //a+b*i
            for(int i=p;i<p+l;i++,w=w*wn){
                tmpx=a[i],tmpy=w*a[i+l];
                a[i]=tmpx+tmpy,a[i+l]=tmpx-tmpy;
            } //↑↑用“蝴蝶操作”优化
        }
    }
}

int main(){ 

    reads(n),reads(m); //↓↓注意从0次开始
    for(int i=0;i<=n;i++) scanf("%lf",&a[i].x);
    for(int i=0;i<=m;i++) scanf("%lf",&b[i].x);
    
    while(len<=(n+m)) len<<=1,L++;
    
    for(int i=0;i<=len;i++) turn[i]=(turn[i>>1]>>1)|((i&1)<<L);
    //↑↑位逆序替换，就找到了对应的turn位置
     
    /*  实现思路：系数表示法—>点值表示法—>系数表示法。
        后面的1表示要进行的变换是什么类型。
        1表示从系数变为点值，-1表示从点值变为系数。 */

    FFT(a,1),FFT(b,1); //从系数变为点值
    for(int i=0;i<=len;i++) a[i]=a[i]*b[i];

    FFT(a,-1); for(int i=0;i<=n+m;i++) 
        printf("%d ",(int)(a[i].x/len+0.5)); //四舍五入
}

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<cmath>
#include<map>
using namespace std;
typedef long long ll;

//【p1919】FFT求大整数乘法

void reads(int &x){ //读入优化（正负整数）
    int fa=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')fa=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();}
    x*=fa; //正负号
}

const int N=1000019;

struct complex{ //复数
    double x,y;
    complex(){} //复数的相关运算
    complex(double x,double y){this->x=x,this->y=y;}
    complex friend operator +(complex n1,complex n2)
      {return complex(n1.x+n2.x,n1.y+n2.y);}
    complex friend operator -(complex n1,complex n2)
      {return complex(n1.x-n2.x,n1.y-n2.y);}
    complex friend operator *(complex n1,complex n2)
      {return complex(n1.x*n2.x-n1.y*n2.y,n1.x*n2.y+n1.y*n2.x);}
}a[N],b[N],tmpx,tmpy,wn,w;

const double pi=3.1415926535897632;

int n,m,turn[N],len=1,L=-1;

char s1[N],s2[N]; int aa=0,bb=0,ans[N];

void FFT(complex *a,int typ){
    for(int i=0;i<len;i++)
        if(i<turn[i]) swap(a[i],a[turn[i]]);
    for(int l=1;l<len;l<<=1){
        wn=complex(cos(pi/l),typ*sin(pi/l));
        for(int p=0;p<len;p+=(l<<1)){
            w=complex(1,0); //a+b*i
            for(int i=p;i<p+l;i++,w=w*wn){
                tmpx=a[i],tmpy=w*a[i+l];
                a[i]=tmpx+tmpy,a[i+l]=tmpx-tmpy;
            } //↑↑用“蝴蝶操作”优化
        }
    }
}

int main(){ //把每一位看成一个系数，最后再整合

    reads(n); scanf("%s%s",s1,s2);
    for(int i=n-1;i>=0;i--) a[aa++].x=s1[i]-48;
    for(int i=n-1;i>=0;i--) b[bb++].x=s2[i]-48;
    
    while(len<(n+n)) len<<=1,L++;
    
    for(int i=0;i<=len;i++) turn[i]=(turn[i>>1]>>1)|((i&1)<<L);
    //↑↑位逆序替换，就找到了对应的turn位置
     
    /*  实现思路：系数表示法—>点值表示法—>系数表示法。
        后面的1表示要进行的变换是什么类型。
        1表示从系数变为点值，-1表示从点值变为系数。 */

    FFT(a,1),FFT(b,1); //从系数变为点值
    for(int i=0;i<=len;i++) a[i]=a[i]*b[i]; //记录乘积答案

    FFT(a,-1); //把乘积答案转化为各位置的系数
    for(int i=0;i<=len;i++){
        ans[i]+=(int)(a[i].x/len+0.5); //系数整合为大整数 
        if(ans[i]>=10) ans[i+1]+=ans[i]/10,ans[i]%=10,
            len+=(i==len); //判断是否要多一位
    } while(!ans[len]&&len>=1) len--; //删除前导零

    len++; while(--len>=0) cout<<ans[len]; //输出答案
}

数论变换

根据原根和费马小定理的规律，可以推出：

如果 n = 2^k，则也可以利用与 FFT 类似的方式快速的计算数论变换。

快速数论变换对所选取的素数模数有着特殊的要求，即满足：2^k = n | p − 1。

比如常见的模数：

p（UOJ）= 998244353 = 7 · 17 · 2^23 + 1

就是一个可以用于快速数论变换的模数。

FFT 可以用来计算多项式乘法。卷积可以写成多项式乘法，因此 FFT 可以计算序列的卷积。

【例题】洛谷p3338 力

【解题思路】

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<cmath>
#include<map>
using namespace std;
typedef long long ll;

//【p3338】力

void reads(int &x){ //读入优化（正负整数）
    int fa=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')fa=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+s-'0';s=getchar();}
    x*=fa; //正负号
}

const int N=(1<<18)+10;

struct complex{ //复数
    double x,y;
    complex(){} //复数的相关运算
    complex(double x,double y){this->x=x,this->y=y;}
    complex friend operator +(complex n1,complex n2)
      {return complex(n1.x+n2.x,n1.y+n2.y);}
    complex friend operator -(complex n1,complex n2)
      {return complex(n1.x-n2.x,n1.y-n2.y);}
    complex friend operator *(complex n1,complex n2)
      {return complex(n1.x*n2.x-n1.y*n2.y,n1.x*n2.y+n1.y*n2.x);}
}a[N],b[N],tmpx,tmpy,wn,w;

const double pi=3.1415926535897632;

int n,turn[N],len=1,L=-1;

double out[N],q[N];

void FFT(complex *a,int typ){
    for(int i=0;i<len;i++)
        if(i<turn[i]) swap(a[i],a[turn[i]]);
    for(int l=1;l<len;l<<=1){
        wn=complex(cos(pi/l),typ*sin(pi/l));
        for(int p=0;p<len;p+=(l<<1)){
            w=complex(1,0); //a+b*i
            for(int i=p;i<p+l;i++,w=w*wn){
                tmpx=a[i],tmpy=w*a[i+l];
                a[i]=tmpx+tmpy,a[i+l]=tmpx-tmpy;
            } //↑↑用“蝴蝶操作”优化
        }
    }
}

int main(){ 

    reads(n); for(int i=1;i<=n;i++) scanf("%lf",&q[i]);
    
    for(int i=1;i<=n;i++) a[i].x=q[i],b[i].x=1.0/i/i;
    //把 b[i].x=1.0/i/i 换成 1.0/(i*i) 会被卡精度↑↑
    
    while(len<=((n+1)<<1)) len<<=1,L++;
    
    for(int i=0;i<len;i++) turn[i]=turn[i>>1]>>1|(i&1)<<L;
    //↑↑位逆序替换，就找到了对应的turn位置
     
    /*  实现思路：系数表示法—>点值表示法—>系数表示法。
        后面的1表示要进行的变换是什么类型。
        1表示从系数变为点值，-1表示从点值变为系数。 */

    FFT(a,1),FFT(b,1); //从系数变为点值
    for(int i=0;i<len;i++) a[i]=a[i]*b[i];

    FFT(a,-1); //从点值变为系数
    for(int i=1;i<=n;i++) out[i]+=a[i].x/len;
    for(int i=0;i<len;i++) a[i]=complex(0,0);
    for(int i=1;i<=n;i++) a[n+1-i]=complex(q[i],0);

    FFT(a,1); //从系数变为点值
    for(int i=0;i<len;i++) a[i]=a[i]*b[i];

    FFT(a,-1); //从点值变为系数
    for(int i=1;i<=n;i++) out[n+1-i]-=a[i].x/len;
    
    for(int i=1;i<=n;i++) printf("%.3lf
",out[i]);
}

矩阵的各种运算

矩阵的转置

矩阵的运算

两个矩阵的和或差定义为对应元素求和或差。

用一个数乘矩阵定义为用其乘以矩阵中的每个数。

矩阵乘法

线性递推数列

 

邻接矩阵

简单图 G 的邻接矩阵 A = (aij) 是一个 | V | 阶的方阵，

其中若顶点 i 到顶点 j 有边则 aij = 1，反之 aij = 0。

图的邻接矩阵在一些图上的计数问题中有应用。

若 G 不是简单图，可以令 aij 表示顶点 i 到顶点 j 的边的数量。

图上路径计数

给一个有向图 G（可能有重边和自环），对于所有点对 (u, v)，

计算 u 到 v 的长度为 k 的路径有多少。

记所求答案为 f (k, u, v)，并令 a uv 表示顶点 u 到顶点 v 的边的数量，

则有：可以发现这是矩阵的形式。

线性方程组

行初等变换

一个矩阵的行初等变换指的是对一个矩阵施行的下列变换：

1. 交换矩阵的两行；

2. 用一个非零的数乘矩阵的某一行；

3. 用一个数乘以矩阵的某一行后加到另一行。

对方程组的增广矩阵作行初等变换不改变对应方程组的解。

我们希望通过行初等变换将矩阵化为便于求解的形式。

一个思路就是将矩阵化为阶梯型矩阵。这个过程就是 高斯消元 。

• 我们从左到右考虑系数矩阵的每一列。
• 对于第 i 列，找到一行使第 i 个元素非 0，将此行与第 i 行交换，aii ！= 0。
• 然后我们对于每个 j 满足 j > i，将第 i 行乘以 −aji/aii 加到第 j 行上。
• 经过这样的操作，对于 j > i，有 aji = 0。
• 依次考虑 1 ≤ i ≤ n 就完成了高斯消元的过程。时间复杂度为O(n^3)。

可以发现，高斯消元之后，第 n 个方程已经给出了第 n 个未知数的值。

将第 n 个未知数的值代入第 n − 1 个方程，就得到了第 n − 1 个未知数的值。

......反复如此做，就得到了所有未知数的值。

Q：如果在某一步的时候找不到对应的 aii！ = 0 怎么办？

A：这说明方程组没有唯一解，有可能是无解或者无穷多组解。

异或方程组

考虑取值为 0 或 1 的变量 x1, . . . , xn，给定 n 个条件，

每个条件选出一些变量并给出他们的异或值。

这其实就是 mod 2 意义下的线性方程组，也可以用高斯消元来解。

注意消元的过程其实就是将一个方程异或到另一个方程上，可用 bitset优化。

概率初步

随机变量与期望

期望的线性性质

图上的概率及期望问题

                       ——时间划过风的轨迹，那个少年，还在等你。