机器学习基石 之 线性回归（Linear Regression）

线性回归（Linear Regression)

理论实现

最简单的想法是

[y approx sum _ { i = 0 } ^ { d } w _ { i } x _ { i } ]

线性回归的假设函数为: (h(mathrm{x}) = mathrm{w}^{T} mathrm{x})。类似于 perceptron 只是没有 sign 函数。

线性回归的目的是找到一个方差最小的超平面（线条），所以误差检测使用流行的方差（squared error）

[operatorname{err}( ilde{y}, y) =( ilde{y}-y)^{2} ]

in-sample / out-of-sample 误差为：

[E _ { mathrm { in } } ( mathbf { w } ) = frac { 1 } { N } sum _ { n = 1 } ^ { N } ( underbrace { h left( mathbf { x } _ { n } ight) } _ { mathbf { w } ^ { T } mathbf { x } _ { n } } - y _ { n } ) ^ { 2 }\ E _ { ext {out } } ( mathbf { w } ) = underset { ( mathbf { x } , y ) sim P } { mathcal { E } } left( mathbf { w } ^ { T } mathbf { x } - y ight) ^ { 2 } ]

为了表示方便写出 in-sample 误差 (E _ { mathrm { in } } ( mathbf { w } )) 的矩阵形式：

[egin{aligned} E _ { mathrm { in } } ( mathbf { w } ) & = frac { 1 } { N } sum _ { n = 1 } ^ { N } left( mathbf { w } ^ { T } mathbf { x } _ { n } - y _ { n } ight) ^ { 2 } = frac { 1 } { N } sum _ { n = 1 } ^ { N } left( mathbf { x } _ { n } ^ { T } mathbf { w } - y _ { n } ight) ^ { 2 } \ &= frac { 1 } { N } left| egin{array} { c } mathbf { x } _ { 1 } ^ { T } mathbf { w } - y _ { 1 } \ mathbf { x } _ { 2 } ^ { T } mathbf { w } - y _ { 2 } \ cdots \ mathbf { x } _ { N } ^ { T } mathbf { w } - y _ { N } end{array} ight| ^ { 2 }\ &= frac { 1 } { N } left| left[ egin{array} { c } - - mathbf { x } _ { 1 } ^ { T } - - \ - - mathbf { x } _ { 2 } ^ { T } - - \ cdots \ - - mathbf { x } _ { N } ^ { T } - - end{array} ight] mathbf { w } - left[ egin{array} { c } y _ { 1 } \ y _ { 2 } \ cdots \ y _ { N } end{array} ight] ight| ^ { 2 }\ & = frac { 1 } { N } | underbrace { X } _ { N imes d + 1 } underbrace { mathbf { w } } _ { d + 1 imes 1 } - underbrace { mathbf { y } } _ { N imes 1 } | ^ { 2 } end{aligned} ]

那现在的任务便是

[min _ { w } E _ { i n } ( mathbf { w } ) = frac { 1 } { N } | X mathbf { w } - mathbf { y } | ^ { 2 } ]

此时的 (E _ { mathrm { in } } ( mathbf { w } )) 曲线如下：

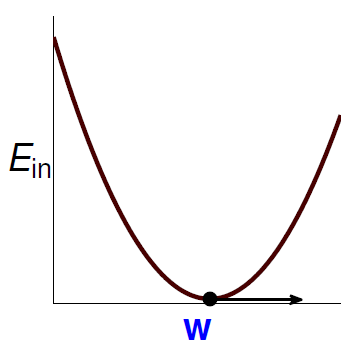
由公式和图形可知 (E _ { mathrm { in } } ( mathbf { w } )) 是连续（continuous），可微（differentiable），凸（convex）的。那么最小化 (E _ { mathrm { in } } ( mathbf { w } )) 的必要条件（necessary condition）是：

[ abla E _ { ext {in } } ( mathbf { w } ) equiv left[ egin{array} { c } frac { partial E _ { ext {in } } } { partial w _ { 0 } } ( mathbf { w } ) \ frac { partial E _ { ext {in } } } { partial w _ { 1 } } ( mathbf { w } ) \ cdots \ frac { partial E _ { ext {in } } } { partial w _ { d } } ( mathbf { w } ) end{array} ight] = left[ egin{array} { c } 0\ 0\ cdots\ 0\ end{array} ight] ]

那么现在的任务便是找出(mathbf{w}_{LIN}) 使得 ( abla E _ { ext {in } }(mathbf{w}_{LIN}) = 0)。

矩阵形式的多项式展开为：

[E _ { mathrm { in } } ( mathbf { w } ) = frac { 1 } { N } | mathrm { Xw } - mathbf { y } | ^ { 2 } = frac { 1 } { N } left( mathbf { w } ^ { T } mathbf { X } ^ { T } mathbf { X } mathbf { w } - 2 mathbf { w } ^ { T } mathbf { X } ^ { T } mathbf { y } + mathbf { y } ^ { T } mathbf { y } ight) ]

所以其矩阵求导结果为（可类比于非向量形式）：

[ abla E _ { ext {in } } ( mathbf { w } ) = frac { 2 } { N } left( X ^ { T } X mathbf { w } - X ^ { T } mathbf { y } ight) ]

那么现在令其为零可求得：

[mathbf { w } _ { mathrm { LIN } } = mathrm { X } ^ { dagger } mathbf { y } ]

其中 ({ dagger }) 代表伪逆，当(mathrm { X }^{T} mathrm { X })非奇异时也可使用 (mathbf { w } _ { mathrm { LIN } } = (mathrm { X }^{T} mathrm { X })^{-1} mathrm { X } mathbf { y }) 求得。

总结一下Linear Regression算法的实现步骤为：

1. 通过数据集，获取输入矩阵（input matrix）和输出向量（output vector）

[X = underbrace{left[ egin{array} { c } - - mathbf { x } _ { 1 } ^ { T } - - \ - - mathbf { x } _ { 2 } ^ { T } - - \ cdots \ - - mathbf { x } _ { N } ^ { T } - - end{array} ight]}_{N imes (d+1)} \,\,\,\,\,\,\,\,\,\, mathbf{y} = underbrace{left[ egin{array} { c } y _ { 1 } \ y _ { 2 } \ cdots \ y _ { N } end{array} ight]}_{N imes 1} \ ]

2. 计算伪逆 (pseudo-inverse）(underbrace{mathrm { X } ^ { dagger }}_{(d+1) imes N})
3. return (underbrace{mathbf { w } _ { mathrm { LIN } }}_{d+1 imes 1} = mathrm { X } ^ { dagger } mathbf { y })

Hat Matrix 的几何视角

下面公式的意义为对于服从统一分布的数据，经过多次抽取后训练误差的平均 (overline{E _ { ext {in } }})，而其大概长下面这个样子是

[overline{E _ { ext {in } }} = underset { mathcal { D } _ { sim P N } } { mathcal { E } } left{ E _ { ext {in } } left( mathbf { w } _ { ext {LIN } } ext { w.r.t. } mathcal { D } ight) ight} = ext{noise level} cdot left( 1 - frac { d + 1 } { N } ight) ]

[egin{aligned} E _ { mathrm { in } } left( mathbf { w } _ { mathrm { LIN } } ight) = frac { 1 } { N } | mathbf { y } - underbrace { hat { mathbf { y } } } _ { ext {predictions } } | ^ { 2 } & = frac { 1 } { N } | mathbf { y } - mathrm { X } underbrace { mathrm { X } ^ { dagger } mathbf { y } } _ { mathrm { W } _ { mathrm { LIN } } } | ^ { 2 }\ & = frac { 1 } { N } | (underbrace{mathbf { I }}_{ ext{identity}} - mathrm { X } underbrace { mathrm { X } ^ { dagger }) mathbf { y } } _ { mathrm { W } _ { mathrm { LIN } } } | ^ { 2 } end{aligned} ]

这里叫 (mathrm { X } mathrm { X } ^ {dagger}) 为 hat matrix (H)。

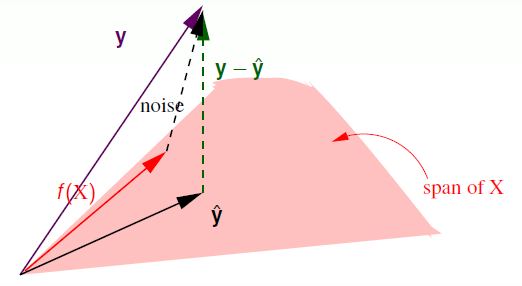
经过上述推导，可以得出 (hat {mathbf { y } }= mathrm { X }mathbf { w } _ { mathrm { LIN } }) ，即 (hat {mathbf { y } }) 是 (mathbf{x}_{n}) 的线性组合，也是由 (mathbf{x}_{n}) 展开的空间中的一个向量；同时由于 (mathbf { y }) 是独立于该空间外的一个向量，同时由于 (mathbf { y }-hat {mathbf { y } }) 最小，那么 (mathbf { y }-hat {mathbf { y } }) 必然垂直于该空间。进而可以得出 (hat {mathbf { y } }) 是 (mathbf { y }) 在该空间上的一个投影，而投影矩阵便是 (H)。所以 (I - H) 也可以看作 (mathbf { y }) 向 (mathbf { y }-hat {mathbf { y } }) 映射的投影矩阵。

可以推导得 ( ext{trace}(I - H) = N - (d + 1))，不详细解释。物理意义是将一个(N)维向量向(d+1)维空间做投影时，其余数的自由度最多有只有(N - (d + 1))。

那么 noise 向量向该空间内投影后取余仍然是 (（ mathbf { I } - mathrm { H } ） ext{noise} = mathbf { y }-hat {mathbf { y } }) ，即：

[egin{aligned} E _ { ext {in } } left( mathbf { w } _ { mathrm { LIN } } ight) = frac { 1 } { N } | mathbf { y } - hat { mathbf { y } } | ^ { 2 } & = frac { 1 } { N } | ( mathbf { I } - mathrm { H } ) ext { noise } | ^ { 2 } \ & = frac { 1 } { N } ( N - ( d + 1 ) ) {| ext{noise} |} ^ { 2 } \ & = frac { 1 } { N } ( N - ( d + 1 ) ) sigma ^ { 2 } end{aligned} ]

经过理论推导可以得出（这里不详细推导）：

[egin{aligned} overline{E _ { ext {in} }} &= ( 1 - frac { d + 1 } { N } ) sigma ^ { 2 } \ overline{E _ { ext {out} }} &= ( 1 + frac { d + 1 } { N } ) sigma ^ { 2 } end{aligned} ]

将两者绘制出随数据量增加的变化曲线如下：

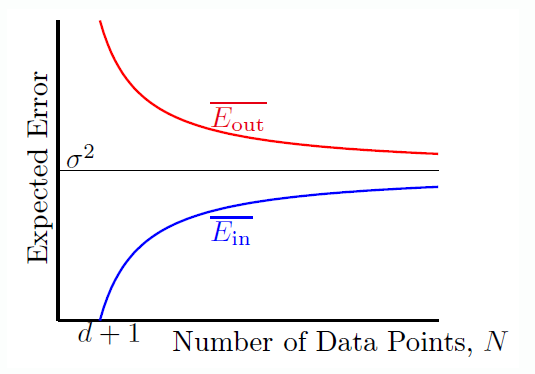
可以看出当 (N ightarrow inf) 时，两者均收敛，且两者之差为 (frac { 2(d + 1) } { N })。类似于 VC bound。

线性回归（Linear Regression）( ightarrow)分类（Classification）

由于 Linear Classification 是一种 NP-Hard 问题，那可以将回归的解决方法用于分类吗？

先对比一下两者的误差测量函数：

[operatorname { err } _ { 0 / 1 } = left| operatorname { sign } left( mathbf { w } ^ { T } mathbf { x } ight) eq y ight| quad ext { err } _ { mathrm { sqr } } = left( mathbf { w } ^ { T } mathbf { x } - y ight) ^ { 2 } ]

绘制出曲线如下：

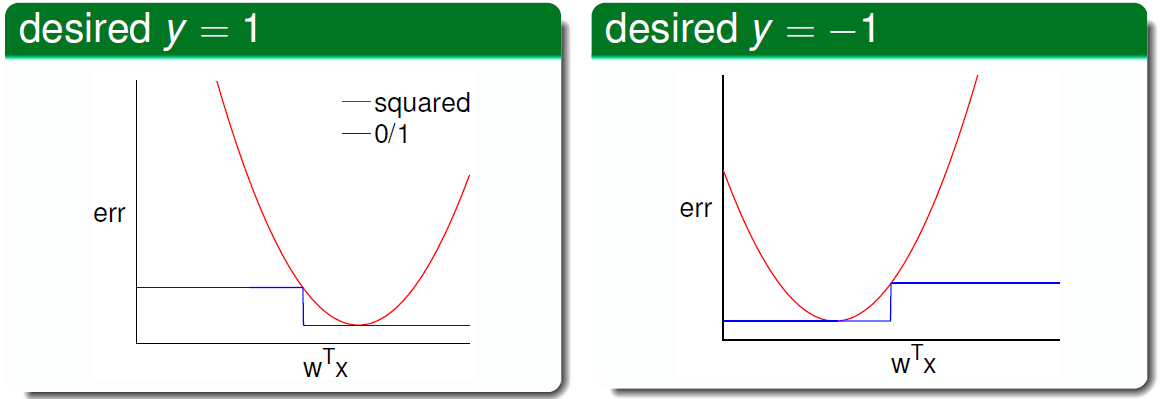
可见(operatorname { err } _ { 0 / 1 } < operatorname { err } _ { ext{sqr} })，所以可以得出：

[egin{aligned} ext{classification } E_{out}(mathbf{w}) & leq ext{classification } E_{in}(mathbf{w}) + sqrt{cdots cdots} \ & leq ext{regression } E_{in}(mathbf{w}) + sqrt{cdots cdots} end{aligned} ]

所以说如果回归误差作为上限很小，那么分类误差也会很小。所以线性回归可以用于分类。

由于存在误差所以可以将(mathbf{w}_{LIN})作为 PLA/Pocket 算法的初始（基础）向量。