emm接下来讲讲splay,个人比较喜欢splay,其主要操作就是伸展旋转,它的应用比较广泛,对于一个有序序列,它可以实现区间翻转,还可以求区间第k大。
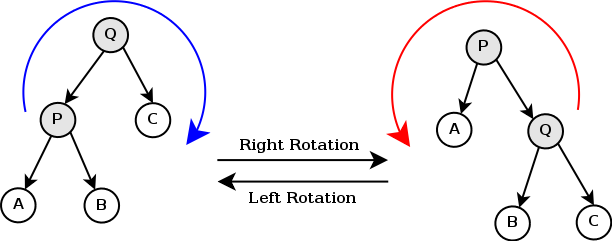
splay的核心操作-旋转(本人的旋转可能与一般旋转有点不一样):
通过上图两种旋转我们可以发现一点点规律:若要rotate(x),先获取x为该父亲的右或左节点p,p为1或0,那么x的(p^1)子节点的父亲指向x的父亲,x的父亲的(p)子节点指向
x的(p^1)子节点,x的父亲只想原有父亲的祖先,同时更新祖先儿子,更新子树大小;我们可以通过循环来使x节点伸展到根;

1 bool get(int x){ 2 return x==p[p[x].f].son[1]; 3 } 4 void rorate(int x){ 5 int f=p[x].f,ff=p[p[x].f].f,opt=get(x); 6 p[f].son[opt]=p[x].son[opt^1]; 7 p[p[x].son[opt^1]].f=f; 8 if(ff) p[ff].son[get(f)]=x; 9 else root=x; 10 11 p[x].f=ff; 12 p[f].f=x; 13 p[x].son[opt^1]=f; 14 // printf("%d %d ",f,x); 15 refresh(f); 16 refresh(x); 17 }
其他的话个人觉得应该没什么好讲的了,删除和插入操作都基本和普通平衡树一样。学会splay后可以去刷下luogu的模板题splay,以下为我的代码:

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 #define maxn 100010 5 struct node{ 6 int size,son[2],f,rev; 7 }p[maxn]; 8 int root,n,m; 9 bool get(int x){ 10 return x==p[p[x].f].son[1]; 11 } 12 void refresh(int x){ 13 if(x){ 14 int size=1; 15 if(p[x].son[0]) size+=p[p[x].son[0]].size; 16 if(p[x].son[1]) size+=p[p[x].son[1]].size; 17 p[x].size=size; 18 } 19 } 20 void build(int l,int r,int f){ 21 if(l>r) return; 22 int mid=(l+r)/2; 23 if(f>mid) p[f].son[0]=mid; 24 else p[f].son[1]=mid; 25 if(f!=mid) p[mid].f=f; 26 p[mid].size=1; 27 if(l==r) return; 28 build(l,mid-1,mid); 29 build(mid+1,r,mid); 30 refresh(mid); 31 } 32 void rorate(int x){ 33 int f=p[x].f,ff=p[p[x].f].f,opt=get(x); 34 p[f].son[opt]=p[x].son[opt^1]; 35 p[p[x].son[opt^1]].f=f; 36 if(ff) p[ff].son[get(f)]=x; 37 else root=x; 38 39 p[x].f=ff; 40 p[f].f=x; 41 p[x].son[opt^1]=f; 42 // printf("%d %d ",f,x); 43 refresh(f); 44 refresh(x); 45 } 46 void rever(int x){ 47 swap(p[x].son[0],p[x].son[1]); 48 p[p[x].son[0]].rev^=1; 49 p[p[x].son[1]].rev^=1; 50 p[x].rev^=1; 51 //printf("%d %d ",p[x].son[0],p[x].son[1]); 52 } 53 void splay(int x,bool k){ 54 if(!k){ 55 while(p[x].f){ 56 rorate(x); 57 root=x; 58 } 59 root=x; 60 } 61 else{ 62 while(p[p[x].f].f){ 63 rorate(x); 64 } 65 p[root].son[1]=x; 66 } 67 } 68 int find(int x){ 69 int now=root; 70 while(1){ 71 // printf("%d %d ",x,now); 72 if(p[now].rev) rever(now); 73 if(p[p[now].son[0]].size>=x){ 74 now=p[now].son[0]; 75 } 76 else{ 77 if(p[p[now].son[0]].size==x-1) return now; 78 x-=p[p[now].son[0]].size+1; 79 now=p[now].son[1]; 80 } 81 } 82 } 83 void dfout(int x){ 84 if(p[x].rev) rever(x); 85 if(p[x].son[0]) dfout(p[x].son[0]); 86 if(x>1&&x<n+2) printf("%d ",x-1); 87 if(p[x].son[1]) dfout(p[x].son[1]); 88 } 89 int main() 90 { 91 int l,r; 92 scanf("%d %d",&n,&m); 93 root=(n+3)/2; 94 build(1,n+2,root); 95 while(m--){ 96 scanf("%d %d",&l,&r); 97 if(l==r) continue; 98 l=find(l); 99 r=find(r+2); 100 splay(l,0); 101 splay(r,1); 102 p[p[p[root].son[1]].son[0]].rev^=1; 103 } 104 dfout(root); 105 return 0; 106 }
