来源:https://blog.csdn.net/summer_dew/article/details/81557331
参考:《数据结构》严蔚敏
关节点
什么是关节点
【关节点】
删除顶点V 与 =>图不再是连通图了 => 顶点V就叫关节点 V上的所有边
【连通图】图中的任意两点,都有路可以连通
例子:
- 将 顶点a 与 a的所有边删除 =>剩下的顶点所构成的图被分成两个部分(连通分量) => a是关节点
- 将 顶点c 与 c的所有边删除 =>剩下的顶点所构成的图被分成两个部分(连通分量) => c是关节点
- 将 顶点b 与 b的所有边删除 =>剩下的顶点所构成的图还是连通图 => b不是关节点
【解释】怎么看v是不是关节点 => v死后,其他结点是不是相互找到 => 不能的话,那v就是关键的东西,它死了,你就找不到你上面的人了 => v是关节点
关节点的特征
定性的了解关节点,方便之后讨论如何求它 => 利用DFS生成树
看生成树中各个顶点的类型:
- 根结点
- 其他结点
类型一:根结点a
【△】如果 根结点a有两个或两个以上的分支 => a就是关节点
【解释】生成树有两棵子树意味着什么?<= 两个子树之间是互不相同的
【证明】生成树有两棵子树w1,w2 => 若 w1中有一个顶点v1 与 w2中一个结点v2 存在一条边,那么!在遍历w1的时候,就会遍历到v2 => v2所属的子树w2 不会成为 根结点的一个子树,而是被挂在w1下
【结论】生成树中根结点的子树各不相通,除了通过根结点本身
类型二:其他结点
【△】若 v没有和它祖先相同的回边 => v是关节点
【解释】实际上,就是v死后,其他人是不是能够相互找到(可以通过中间人找)
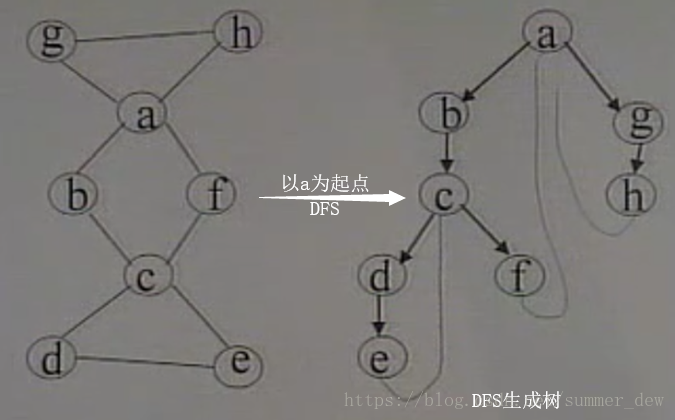
【例子】左边是图,右边是一个DFS生成树。
从右图中,可以看到,DFS树上除了自身的边,还有一些边(e-c,f-a,h-a)
这些边是生成DFS树时,没有走过的边,这里叫做回边(e-c,f-a,h-a)
=> 可以看出,
- 如果d死了,e还可以通过c,找到别的人(所有人);
- 如果g死了,h可以通过a找到别的人(所有人)
- 如果c死了, f可以通过a找到其他人(不是所有人),但不能找到d和e,因为de与其他结点失联了 => c是关节点
如何求关节点
定性 到 定量的求法
类型一:生成树的根
若从 DFS生成树 的 根结点 的 一个边 出发DFS
- 能够访问到所有结点 => 只有一个子树 => 根 不是关节点
- 若不能访问到所有结点 => 有好几个子树 => 根 是关节点
类型二:其他结点
判断v是不是关节点:
- visited[v]为v的访问次序
- 一个函数low()
- 如果v有一个孩子w,满足low[w] ≥ visited[v],则v就是关节点
实现:
-
怎么判断v是不是关节点?
看到公式low() => 求v是不是,得看它的子节点 => 所以是退回到v的时候来判断v是不是 => DFS执行完之后来判断【代码中位置①】 -
low()怎么在代码中实现呢?
先定义一个min【代码中位置②】,low(v)中有三个量,谁出现了就和min进行比较,取最小- visited[v]最先出现:遍历到v的时候就出现了【代码中位置③】
- low[w]:遍历到w的时候,可以计算,计算完,让它与min比较【代码中位置④】
- visited[k]:k为回边,即第二次遍历到k结点的时候即是回边时【代码中位置⑤】
1 //从 第v0顶点 出发DFS,查找并输出关节点 2 void DFSArticul(ALGraph G, int v0) { 3 //v0是第count个访问的顶点 4 visited[v0] = min = ++count; // --②、③ 5 for (p=G.vertices[v0].firstarc; p; p=p->nextarc) { //对v0的每个邻接点进行检查 6 w = p->adjvex; //w是v0的邻接点 7 if (visited[w] == 0) { //之前都没有访问过 8 DFSArticul(G, w); 9 if (low[w] < min) min = low[w]; // --④ 10 if (low[w] >= visited[v0]) printf(v0是关节点); // --① 11 } else if (visited[w] < min) { //w已经访问过了,说明w是回边 12 min = visited[w]; // --⑤ 13 } 14 } 15 low[v0] = min; //设置v0的low值 16 }
总代码 ( 来自《数据结构》严蔚敏 )
1 count=1; //定义为全局变量 2 void FindArticul(ALGraph G) { 3 visited[0]=1; //设定邻接表上0号顶点为 生成树的根 4 for (i=1; i<G.verxum; ++i) visited[i] = 0; //初始化,其余点没有访问 5 p = G.vertices[0].firstarc; v = p->adjvex; //取 根的第一个邻接点 6 DFSArticul(G,v); //开始DFS 7 if (count<G.vexnum) { 8 printf("根是关节点"); //根是关节点,输出相应信息 9 while (p->nextarc) { 10 p = p->nextarc; v = p->adjvex; 11 if (visited[v]==0) DFSArticul(g,v); 12 } 13 } 14 } 15 //从 第v0顶点 出发DFS,查找并输出关节点 16 void DFSArticul(ALGraph G, int v0) { 17 //v0是第count个访问的顶点 18 visited[v0] = min = ++count; // --②、③ 19 for (p=G.vertices[v0].firstarc; p; p=p->nextarc) { //对v0的每个邻接点进行检查 20 w = p->adjvex; //w是v0的邻接点 21 if (visited[w] == 0) { //之前都没有访问过 22 DFSArticul(G, w); 23 if (low[w] < min) min = low[w]; // --④ 24 if (low[w] >= visited[v0]) printf(v0是关节点); // --① 25 } else if (visited[w] < min) { //w已经访问过了,说明w是回边 26 min = visited[w]; // --⑤ 27 } 28 } 29 low[v0] = min; //设置v0的low值 30 }
重(双)连通图
【重(双)连通图】没有关节点的连通图为双连通图
【解释】前提:图为连通图 => 如果从图中删除任何一个顶点 => 其他顶点之间都能相互通讯,即它还是一个连通图 => 这个连通图 就叫 重(双)连通图