POJ1635 Subway tree systems
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 5470 | Accepted: 2248 |
Description
Some major cities have subway systems in the form of a tree, i.e. between any pair of stations, there is one and only one way of going by subway. Moreover, most of these cities have a unique central station. Imagine you are a tourist in one of these cities and you want to explore all of the subway system. You start at the central station and pick a subway line at random and jump aboard the subway car. Every time you arrive at a station, you pick one of the subway lines you have not yet travelled on. If there is none left to explore at your current station, you take the subway line back on which you first came to the station, until you eventually have travelled along all of the lines twice,once for each direction. At that point you are back at the central station. Afterwards, all you remember of the order of your exploration is whether you went further away from the central station or back towards it at any given time, i.e. you could encode your tour as a binary string, where 0 encodes taking a subway line getting you one station further away from the central station, and 1 encodes getting you one station closer to the central station.
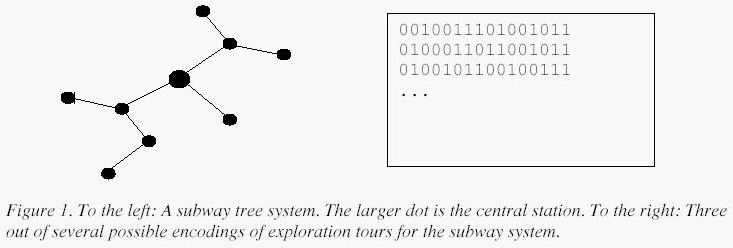

Input
On the first line of input is a single positive integer n, telling the number of test scenarios to follow.Each test scenario consists of two lines, each containing a string of the characters '0' and '1' of length at most 3000, both describing a correct exploration tour of a subway tree system.
Output
exploration tours of the same subway tree system, or the text "different" if the two strings cannot be exploration tours of the same subway tree system.
Sample Input
2 0010011101001011 0100011011001011 0100101100100111 0011000111010101
Sample Output
same different
***************************************************
题目大意:给了两个字符串作为有根树的遍历,向下为0,向上为1,也就是树的最小表示,然后判断两棵树是否同构。
解题思路:纯正的树的最小表示来判断树是否同构参见博客http://www.byvoid.com/blog/directed-tree-bracket-sequence/。
然而,这样做的话速度会比较慢。然后我网上看到了很多人用了一个奇葩的方式,很多人,都是同一种方式:他们首先根据这个树的最小表示来建图,然后,在每个节点记录这个节点的深度和这个节点的子树的节点个数,然后排序判断是否一样,如果一样就当两棵树同构。那么多人都用这个方法,我一开始以为是什么高级的方法,询问了光神后才知道这个方法是唬人用的,真心是因为数据弱才AC。我擦,那些人都是怎么吃饭,看到速度快的代码就照搬照抄,害得我去研究了一下午。然后我用了树的hash方式过的这题,虽然hash是概率算法,但是比网上那些人的方法靠谱多了。
//#pragma comment(linker, "/STACK:65536000")
#include <map>
#include <stack>
#include <queue>
#include <math.h>
#include <vector>
#include <string>
#include <fstream>
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#define N 3005
#define M
#define E
#define inf 0x3f3f3f3f
#define dinf 1e10
#define linf (LL)1<<60
#define LL long long
#define clr(a,b) memset(a,b,sizeof(a))
using namespace std;
const int p = 13777;
const int q = 15237;
string s[2];
int h[N],pre[N];
vector<int>gra[2][N];
void build(int g)
{
int now=0,total=1,len=s[g].size();
for(int i=0;i<len;i++)gra[g][i].clear();
for(int i=0;i<len;i++)
if(s[g][i]=='0')
{
pre[total]=now;
gra[g][now].push_back(total);
now=total++;
}
else
now=pre[now];
}
int dfs(int g,int s)
{
int len=gra[g][s].size();
if(len==0)return 1;
vector<int>hash;
hash.clear();
for(int i=0;i<len;i++)
hash.push_back(dfs(g,gra[g][s][i]));
sort(hash.begin(),hash.end());
int ret=1;
for(int i=0;i<len;i++)
ret=(ret^hash[i])*h[i]%q;
return ret;
}
int main()
{
//freopen("/home/axorb/in","r",stdin);
int T;
cin>>T;
srand(16512);
for(int i=0;i<3000;i++)h[i]=rand()%q;
while(T--)
{
cin>>s[0]>>s[1];
build(0);build(1);
if(dfs(0,0)==dfs(1,0))puts("same");
else puts("different");
}
return 0;
}