Codeforces —— Complete Tripartite(1228D)

input

6 11
1 2
1 3
1 4
1 5
1 6
2 4
2 5
2 6
3 4
3 5
3 6

output

1 2 2 3 3 3 

input

4 6
1 2
1 3
1 4
2 3
2 4
3 4

output

-1

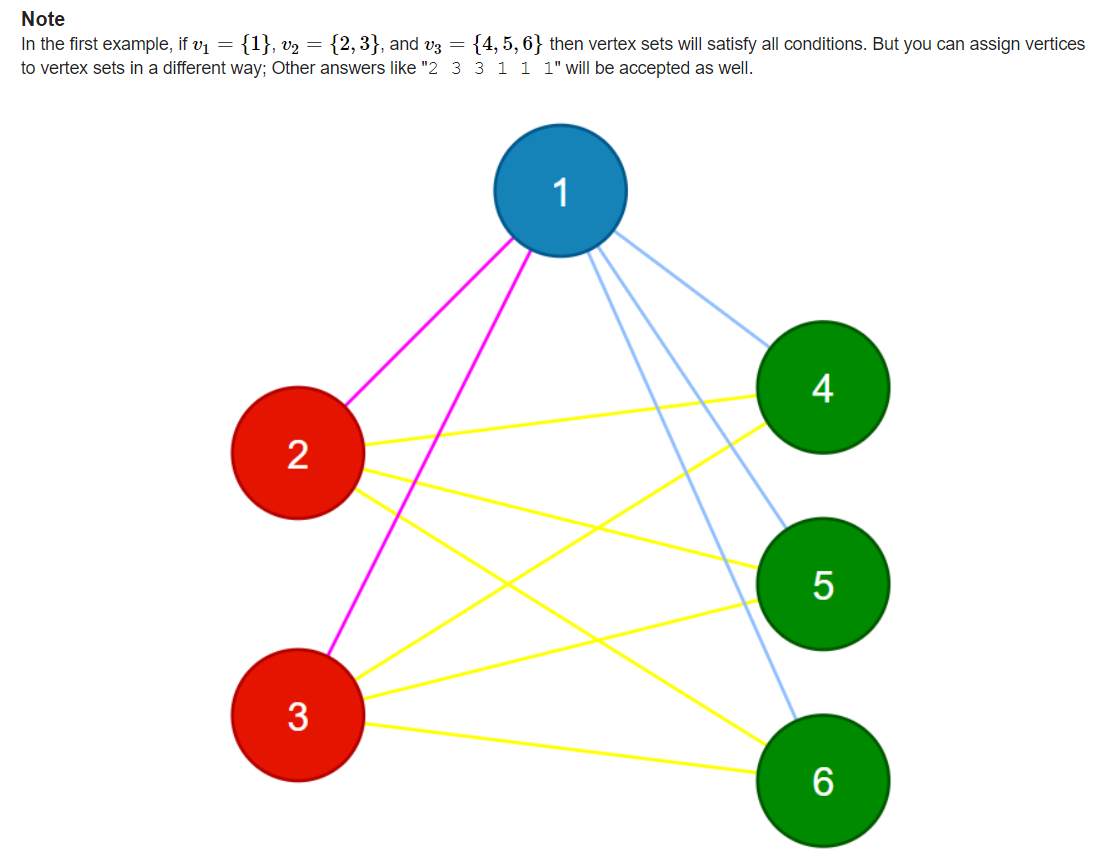
题意

在一张无向图（无自环，不一定联通）中，将所有节点划分为三个集合，每个集合内部的任意
两个点不可以有边，集合件任意两个点必须有边，求出如何划分集合

思路

对于整张图来说:
      第一我们需要满足一共只划分三个集合，所以当集合数量超过3时我们就可以确定无解
      第二对于一个节点x，未与x相连的所有节点的子节点必须与x相连

代码

#pragma GCC optimize(2)
#include<unordered_map>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
#include<vector>
#include<queue>
#include<stack>
#include<cmath>
#include<map>
#include<set>
#define Buff ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
#define rush() int Case = 0; int T; scanf("%d", &T);  while(T--)
#define rep(i, a, b) for(int i = a; i <= b; i ++)
#define per(i, a, b) for(int i = a; i >= b; i --)
#define reps(i, a, b) for(int i = a; b; i ++)
#define clc(a, b) memset(a, b, sizeof(a))
#define readl(a) scanf("%lld", &a)
#define readd(a) scanf("%lf", &a)
#define readc(a) scanf("%c", &a)
#define reads(a) scanf("%s", a)
#define read(a) scanf("%d", &a)
#define lowbit(n) (n&(-n))
#define pb push_back
#define sqr(x) x*x
#define rs x<<1|1
#define y second
#define ls x<<1
#define x first
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int>PII;
const int mod = 1e9+7;
const double eps = 1e-6;
const int N = 1e6+7;
int idx, h[N], e[N<<1], ne[N<<1];
int color[N], vis[N], clo;
int n, m;
void  add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool judge(int x)
{
//    cout << n <<" "<< m <<endl;
    if(clo == 4)    return false;
    color[x] = ++clo;
    int t = 0;
    for(int i = h[x]; ~i; i = ne[i])
    {
        int j = e[i];
//        cout << j <<" ";
        vis[j] = true;  t ++;
    }
//    cout << "t: " << t <<endl;
    rep(i, 1, n)
    {
        if(vis[i] || i == x )    continue;
        int c = 0;
        color[i] = clo;
        for(int j = h[i]; ~j; j = ne[j])
        {
            int p = e[j];
            if(!vis[p]) return false;
            c ++;
        }
//        cout << c <<" "<< t <<endl;
        if(c != t)  return false;
    }
    clc(vis, 0);
    return true;
}
int main()
{
    Buff;
    clc(h, -1);
    cin >> n >> m;
    rep(i, 0, m-1)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }
    for(int i = 1; i <= n; i ++)
        if(!color[i] && !judge(i))  return puts("-1");

    if(clo != 3)    return puts("-1");
    rep(i, 1, n)    cout << color[i] << (i == n ? "
" : " ");
	return 0;
}