题解 CF793E Problem of offices

\[\texttt{题意} \]

\(\quad\)判断是否可以找出一种从根开始遍历的回路，只保留叶子结点后的序列上满足 \(ab\) 之间的距离为 \(\frac{tot}{2}-1\)，\(tot\) 为总叶子结点数，对于 \(c,d\) 也是如此。

\[\texttt{思路} \]

\(\quad\)本题有点氵。

\(\quad\)首先可以发现顺序一定是 \(a,c,b,d\) 或 \(a,d,b,c\)，其实反过来看就是一样的，相邻的之间有某些其他子树。

\(\quad\)另外可以发现对于不含 \(a,b,c,d\) 的根节点的子树，它们一定是整体插入的，即可以看做一个整体。而含 \(a,b,c,d\) 的子树中，这里还需要另外讨论。

\(\quad\)发现这是一个背包问题，设 \(tot\) 为总叶子结点数，找出 \(a,b\) 之间是否有可能塞下刚好为 \(\frac{tot}{2}-1\) 的大小，对于其他子树选或不选，选就整体加，对于包含 \(a,b\) 的子树，就像分组背包一样，发现不能直接选择一个数 \(i\in[0,x-1]\) ，这里 \(x\) 表示含 \(a\) 的子树的叶子结点数,如下图所示，\(a\) 不能在子树 \(2\) 中第 \(4\) 次出现，只能第 \(1,2,6,7\) 次出现。(这里的出现只考虑叶子结点)

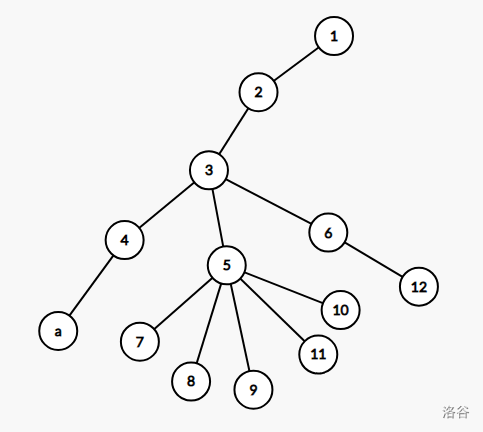
\(\quad\)可以从 \(a\) 开始向上走，对于 \(a\) 的某个祖先，TA的其他儿子的子树大小也可以像之前的背包一样选择(不包括含 \(a\) 的子树，子树大小指叶子结点数)，其实 \(1\) 也是 \(a\) 的祖先，可以一样考虑。

\(\quad\)显然如果 \(a,b,c,d\) 中任意一个的子树大小要小于 \(\frac{tot}{2}\) ，且 \(tot\) 要为偶数才有解。

\(\quad\)这里我先找出 \(a,b,c,d\) 各自的子树，用 bitset 维护答案，\(ab\) 表示 \(a,b\) 之间可能的放下的叶子结点个数，\(cd\) 表示 \(c,d\) 之间可能的放下的叶子结点个数。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<bitset>
#define re register int
#define il inline
using namespace std;
il int read()
{
  int x=0,f=1;char ch=getchar();
  while(!isdigit(ch)&&ch!='-')ch=getchar();
  if(ch=='-')f=-1,ch=getchar();
  while(isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
  return x*f;
}
il void print(int x)
{
  if(x<0)putchar('-'),x=-x;
  if(x/10)print(x/10);
  putchar(x%10+'0');
}
const int N=5e3+5;
int n,a,b,c,d,A,B,C,D,cnt,nxt[N],tot,fa[N],go[N],head[N],sz[N];
bitset<N>ab,cd,t;bool vis[N],p[N];
il void Add(int x,int y)
{
	nxt[++tot]=head[x];
	head[x]=tot;go[tot]=y;
}
il void dfs(int x,int pre)
{
	if(!head[x]){
		sz[x]++;tot++;
		if(x==a)vis[pre]=1,a=pre+n;
		else if(x==b)vis[pre]=1,b=pre+n;
		else if(x==c)vis[pre]=1,c=pre+n;
		else if(x==d)vis[pre]=1,d=pre+n;
		return;
	}
	for(re i=head[x],y;i,y=go[i];i=nxt[i])dfs(y,pre),sz[x]+=sz[y];
}
il void dfs2(int x,int op)
{
	if(x==1)return;p[x]=1;
	for(re i=head[x],y;i,y=go[i];i=nxt[i])
	{
		if(p[y])continue;
		if(op)ab|=(ab<<sz[y]);
		else cd|=cd<<sz[y];
	}
	dfs2(fa[x],op);
}
signed main()
{
	n=read();A=a=read();B=b=read();C=c=read();D=d=read();
	for(re i=2,x;i<=n;i++)fa[i]=read(),Add(fa[i],i);
	tot=0;t.set(0);
	for(re i=head[1],y;i,y=go[i];i=nxt[i])
	{
		dfs(y,y);
		if(!vis[y])t|=(t<<sz[y]);
	}
	if(tot&1){puts("NO");return 0;}
	ab=cd=t;p[A]=p[B]=p[C]=p[D]=1;
	dfs2(fa[A],1);dfs2(fa[B],1);dfs2(fa[C],0);dfs2(fa[D],0);
	if((sz[c-n]<=tot/2-1&&ab[tot/2-sz[c-n]-1])&&(sz[b-n]<=tot/2-1&&cd[tot/2-sz[b-n]-1]))puts("YES");
	else puts("NO");
	return 0;
}