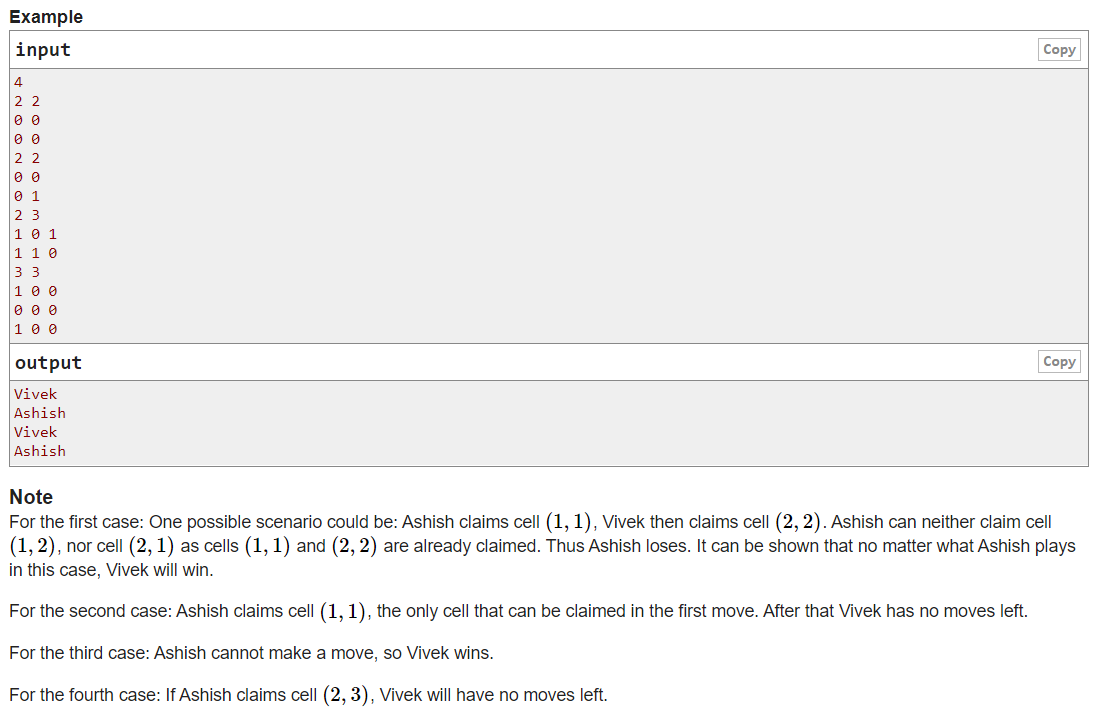
A. Matrix Game
代码：
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 55, M = 1; 4 typedef long long ll; 5 typedef unsigned long long ull; 6 typedef pair<int, int> PII; 7 #define rep(i, x, y) for(i=x;i<=y;i++) 8 #define ref(i, x, y) for(i=x;i>=y;i--) 9 #define MEM(a, x) memset(a, x, sizeof(a)) 10 #define Sca(x) scanf("%d", &x) 11 #define Scl(x) scanf("%lld", &x) 12 #define Scf(x) scanf("%f", &x) 13 #define Sclf(x) scanf("%lf", &x) 14 #define pb push_back 15 #define mp make_pair 16 #define fi first 17 #define se second 18 #define lb lower_bound 19 #define ub upper_bound 20 #define endl ' ' 21 22 int T, n, m; 23 bool col[N], row[N]; 24 25 void solve() 26 { 27 scanf("%d%d", &n, &m); 28 memset(col, 0, sizeof(col)); 29 memset(row, 0, sizeof(row)); 30 for (int i = 1; i <= n; i++) { 31 for (int j = 1; j <= m; j++) { 32 int temp = - 1; 33 Sca(temp); 34 if (temp == 1) { 35 col[j] = row[i] = 1; 36 } 37 } 38 } 39 int cnt1 = 0, cnt2 = 0, cnt = 0; 40 for (int i = 1; i <= n; i++) 41 if (!row[i]) cnt1++; 42 for (int j = 1; j <= m; j++) 43 if (!col[j]) cnt2++; 44 cnt = min(cnt1, cnt2); 45 if (cnt % 2) puts("Ashish"); 46 else puts("Vivek"); 47 } 48 49 int main() 50 { 51 //ios::sync_with_stdio(false); 52 cin >> T; 53 while (T--) { 54 solve(); 55 } 56 return 0; 57 }
B. Trouble Sort
题意：给出长度为n的两个数组a,b。b数组的值只有0，1两种。对于i, j(i != j)，如果b[i] != b[j]，则可以交换a[i]和a[j]以及b[i]和b[j]的位置。提问是否可以通过数次交换使得a数组非递减。
思路：容易知道，对于i, j：①b[i] != b[j] ，则可以直接交换 ②b[i] == b[j], 可以通过一个满足b[k] != b[i]的k，来交换i和j。
所以只要数组中b数组的值不全为0或不全为1就可以排序成有序了。
代码：
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 505, M = 1; 4 typedef long long ll; 5 typedef unsigned long long ull; 6 typedef pair<int, int> PII; 7 #define rep(i, x, y) for(i=x;i<=y;i++) 8 #define ref(i, x, y) for(i=x;i>=y;i--) 9 #define MEM(a, x) memset(a, x, sizeof(a)) 10 #define Sca(x) scanf("%d", &x) 11 #define Scl(x) scanf("%lld", &x) 12 #define Scf(x) scanf("%f", &x) 13 #define Sclf(x) scanf("%lf", &x) 14 #define pb push_back 15 #define mp make_pair 16 #define fi first 17 #define se second 18 #define lb lower_bound 19 #define ub upper_bound 20 #define endl ' ' 21 struct node 22 { 23 int a, b; 24 }a[N]; 25 26 int T, n; 27 bool vis[N]; 28 29 void solve() 30 { 31 cin >> n; 32 int f = 0; 33 for (int i = 1; i <= n; i++) { 34 Sca(a[i].a); 35 if (a[i].a < a[i-1].a) f = 1; 36 } 37 int ff = 0; 38 for (int i = 1; i <= n; i++) { 39 Sca(a[i].b); 40 if (i != 1 && a[i].b != a[i - 1].b) { 41 ff = 1; 42 } 43 } 44 if (!f) { 45 puts("Yes");return; 46 } 47 if (ff) { 48 puts("Yes"); 49 }else{ 50 puts("No"); 51 } 52 53 } 54 55 int main() 56 { 57 //ios::sync_with_stdio(false); 58 cin >> T; 59 while (T--) { 60 solve(); 61 } 62 return 0; 63 }
C. Rotation Matching
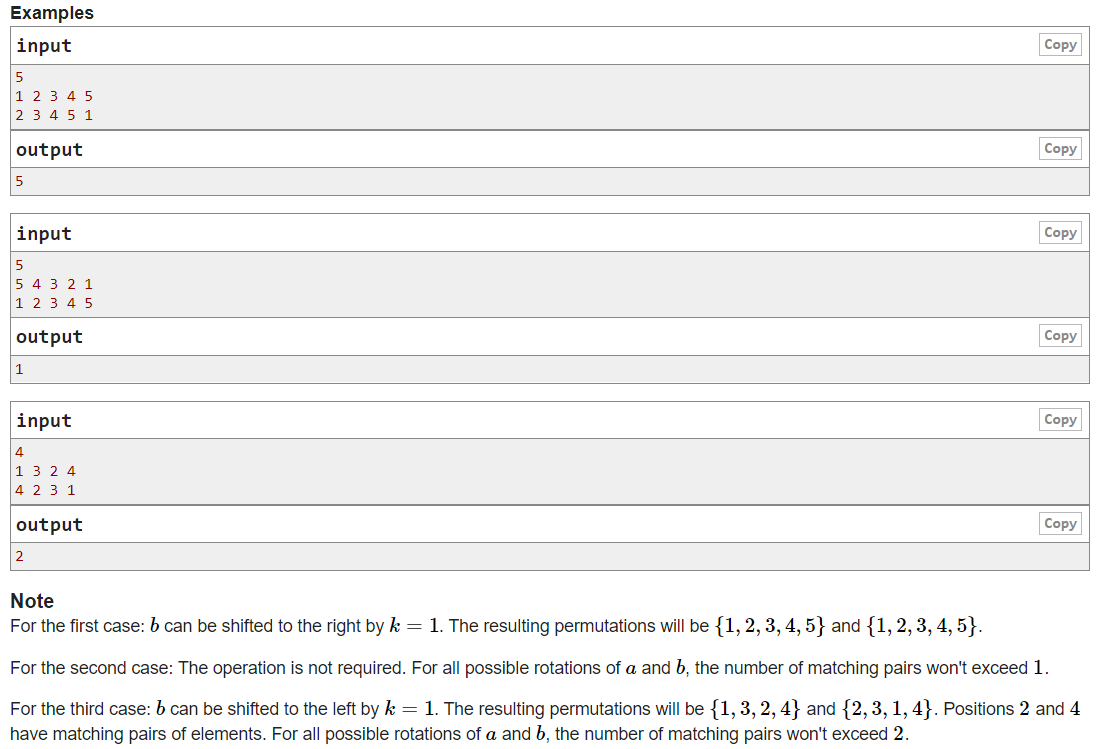
题意：给出一个n，两个序列a，b，每一个序列是1, 2, ......, n的无重复序列，问通过操作可以得到的a[i] == b[i]的i的数量最大是多少。操作：选择一个k，使序列a或b向一个方向移动k次，每次移动的效果
。
思路：拿到题目的第一个想法是暴力，在a数组后面在接一个a数组，然后枚举k，对每一个k计算答案，取最大值。很明显会超时。
容易知道，无论怎么移动，数字之间的相对位置是不会变动的，所以可以记录下每个数字在a, b序列中出现的位置，然后得到可以得到位置的相对差值，相同差值个数最多的差值即为答案。
细节：有时位置相减会是负数，可以用( n + a[i] - b[i] ) % n。
代码：
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 2e5+5, M = 1; 4 typedef long long ll; 5 typedef unsigned long long ull; 6 typedef pair<int, int> PII; 7 #define rep(i, x, y) for(i=x;i<=y;i++) 8 #define ref(i, x, y) for(i=x;i>=y;i--) 9 #define MEM(a, x) memset(a, x, sizeof(a)) 10 #define Sca(x) scanf("%d", &x) 11 #define Scl(x) scanf("%lld", &x) 12 #define Scf(x) scanf("%f", &x) 13 #define Sclf(x) scanf("%lf", &x) 14 #define pb push_back 15 #define mp make_pair 16 #define fi first 17 #define se second 18 #define lb lower_bound 19 #define ub upper_bound 20 #define endl ' ' 21 22 int T, n, a[N << 1], b[N], cnt[N]; 23 bool vis[N]; 24 25 void solve() 26 { 27 cin >> n; 28 for (int i = 1; i <= n; i++) { 29 int k; 30 Sca(k); 31 a[k] = i; 32 } 33 for (int i = 1; i <= n; i++) { 34 int k; 35 Sca(k); 36 b[k] = i; 37 } 38 int mx = 0; 39 for (int i = 1; i <= n; i++) { 40 cnt[(n + a[i] - b[i]) % n]++; 41 } 42 for (int i = 1; i <= n; i++) { 43 mx = max(mx, cnt[i]); 44 } 45 if (n == 1) cout << 1 << endl; 46 else cout << mx << endl; 47 48 } 49 50 void solve2() 51 { 52 cin >> n; 53 for (int i = 1; i <= n; i++) Sca(a[i]); 54 for (int i = 1; i <= n; i++) Sca(b[i]); 55 56 for (int i = 1; i <= n; i++) a[i+n] = a[i]; 57 int ans = 0; 58 for (int i = 1; i <= n; i++) { 59 int cnt = 0; 60 for (int j = 1; j <= n; j++) { 61 if (a[j + i] == b[j]) cnt++; 62 } 63 ans = max(ans, cnt); 64 } 65 cout << ans << endl; 66 } 67 68 int main() 69 { 70 //ios::sync_with_stdio(false); 71 // solve2(); 72 solve(); 73 return 0; 74 }
D. Solve The Maze
题意：给一个n*m的迷宫，. 代表空, #代表墙, G 代表好人, B 代表坏人, 可以把.转换为#使得这个点无法到达。问是否可以通过数次转换，使得所有的好人能到达(n, m)，而所有的坏人无法到达。
思路：对每一个B，影响最小的转换方式肯定是围住上下左右四个点。所以对每一个B转换上下左右，如果B的上下左右有好人，则无法困住这个B，输出No。
围住B以后，要判断每一个G是否可以到达(n, m)，对每一个点dfs显然太慢，可以逆向思维，对(n, m)bfs搜索能到达的点，然后比较能到达的点的G的个数和G的总数，相等即Yes，不然就No。
代码：
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 55, M = 1; 4 typedef long long ll; 5 typedef unsigned long long ull; 6 typedef pair<int, int> PII; 7 #define rep(i, x, y) for(i=x;i<=y;i++) 8 #define ref(i, x, y) for(i=x;i>=y;i--) 9 #define MEM(a, x) memset(a, x, sizeof(a)) 10 #define Sca(x) scanf("%d", &x) 11 #define Scl(x) scanf("%lld", &x) 12 #define Scf(x) scanf("%f", &x) 13 #define Sclf(x) scanf("%lf", &x) 14 #define pb push_back 15 #define fi first 16 #define se second 17 #define lb lower_bound 18 #define ub upper_bound 19 #define endl ' ' 20 21 int T, n, m; 22 int dx[4] = {1, -1, 0, 0}; 23 int dy[4] = {0, 0, 1, -1}; 24 char mp[N][N]; 25 bool vis[N][N]; 26 27 bool judge(int x, int y) 28 { 29 return x > 0 && x <= n && y > 0 && y <= m; 30 } 31 32 void solve() 33 { 34 cin >> n >> m; 35 for (int i = 1; i <= n; i++) 36 scanf("%s", mp[i] + 1); 37 int cnt = 0; 38 for (int i = 1; i <= n; i++) { 39 for (int j = 1; j <= m; j++) { 40 if (mp[i][j] == 'B') { 41 for (int k = 0; k < 4; k++) { 42 int nx = i + dx[k], ny = j + dy[k]; 43 if (!judge(nx, ny)) continue; 44 if (mp[nx][ny] == 'G') { 45 puts("No"); 46 return; 47 }else if (mp[nx][ny] == '.') { 48 mp[nx][ny] = '#'; 49 } 50 } 51 }else if (mp[i][j] == 'G') cnt++; 52 } 53 } 54 55 queue<PII>q; 56 q.push({n, m}); 57 memset(vis, 0, sizeof(vis)); 58 vis[n][m] = 1; 59 if (mp[n][m] == '#' && cnt) { 60 puts("No"); 61 return ; 62 } 63 while (q.size()) { 64 PII now = q.front(); q.pop(); 65 66 for (int i = 0; i < 4; i++) { 67 int nx = now.fi + dx[i], ny = now.se + dy[i]; 68 if (!judge(nx, ny)) continue; 69 if (mp[nx][ny] == 'G' && !vis[nx][ny]) cnt--; 70 if (mp[nx][ny] != '#' && !vis[nx][ny]) q.push({nx, ny}), vis[nx][ny] = 1; 71 } 72 } 73 if (cnt) puts("No"); 74 else puts("Yes"); 75 } 76 77 int main() 78 { 79 //ios::sync_with_stdio(false); 80 cin >> T; 81 while (T--) { 82 solve(); 83 } 84 return 0; 85 }
E. Maximum Subsequence Value
题意：给出一个长度为n的数组，从中挑选k个数字，使价值最大。价值：将每个数字转换为二进制表示，价值为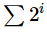
，其中i为满足max(1, k - 2)个第i位为1的位数。（我有点说不清了）
思路：可知k<=3时，只需要有一个数字在第i位上为1即可，所以这时的价值就是这三个数字的或运算（|）。而k>3时，如果原本在第i位上有贡献，那么删去一个第i位为1的数，第i位同样有贡献，并且无贡献的位反而可能因为要求的位数减少使得这个位变为有贡献。所以可以只选三位进行或和，求出其中的最大值。（我也没想到O(n^3)能过，不知道1s里可以有多少次运算）
代码：
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 505, M = 1; 4 typedef long long ll; 5 typedef unsigned long long ull; 6 typedef unsigned int uint; 7 typedef pair<int, int> PII; 8 #define rep(i, x, y) for(i=x;i<=y;i++) 9 #define ref(i, x, y) for(i=x;i>=y;i--) 10 #define MEM(a, x) memset(a, x, sizeof(a)) 11 #define Sca(x) scanf("%d", &x) 12 #define Scl(x) scanf("%lld", &x) 13 #define Scf(x) scanf("%f", &x) 14 #define Sclf(x) scanf("%lf", &x) 15 #define pb push_back 16 #define fi first 17 #define se second 18 #define lb lower_bound 19 #define ub upper_bound 20 #define endl ' ' 21 22 int T, n; 23 ll a[N]; 24 bool vis[N]; 25 26 int main() 27 { 28 //ios::sync_with_stdio(false); 29 cin >> n; 30 for (int i = 1; i <= n; i++) 31 Scl(a[i]); 32 ll i, j, k, res1 = 0, ans = 0; 33 rep(i, 1, n) rep(j, i + 1, n) rep(k, j + 1, n) ans = max(ans, a[i] | a[j] | a[k]); 34 if (n < 3) ans = a[1] | a[2]; 35 cout << ans << endl; 36 return 0; 37 }
F. Swaps Again
题意：给出n长度的两个序列a，b，问能否通过k次操作使得a变成b。操作：选择一个
，使得长度为k的前缀和后缀交换，具体可看看题目的例子。
思路：重点是对称性！对于每一个x以及相对应的y = n - x + 1无论经过多少次操作都是对称的。
因为对于n为奇数时，最中间那项无论如何也无法改变位置，所以当最中间项不同时，肯定无法a转换为b。如果相同时，可忽略这个数，当作偶数个数序列处理。
对于任意一个x, 设 y = n - x + 1。方便起见令x < y即x <= n / 2。当选择k＜x时，明显不变；当k>=x时，x转换后位置x1 = n - k + x, y转换后位置y1 = y - n + k, 得到(x + y) / 2 == (x1 + y1) / 2，即中线都为(n + 1) / 2。
代码：
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 505, M = 1; 4 typedef long long ll; 5 typedef unsigned long long ull; 6 typedef pair<int, int> PII; 7 #define rep(i, x, y) for(i=x;i<=y;i++) 8 #define ref(i, x, y) for(i=x;i>=y;i--) 9 #define MEM(a, x) memset(a, x, sizeof(a)) 10 #define Sca(x) scanf("%d", &x) 11 #define Scl(x) scanf("%lld", &x) 12 #define Scf(x) scanf("%f", &x) 13 #define Sclf(x) scanf("%lf", &x) 14 #define pb push_back 15 #define fi first 16 #define se second 17 #define lb lower_bound 18 #define ub upper_bound 19 #define endl ' ' 20 21 int T, n, a[N], b[N]; 22 bool vis[N]; 23 24 void solve() 25 { 26 vector <PII> va, vb; 27 cin >> n; 28 for (int i = 1; i <= n; i++) Sca(a[i]); 29 for (int j = 1; j <= n; j++) Sca(b[j]); 30 31 if (n % 2 && a[n / 2 + 1] != b[n / 2 + 1]) { 32 puts("No"); 33 return; 34 } 35 for (int i = 1; i <= n / 2; i++) { 36 if (a[i] > a[n - i + 1]) swap(a[i], a[n - i + 1]); 37 if (b[i] > b[n - i + 1]) swap(b[i], b[n - i + 1]); 38 va.pb({a[i], a[n - i + 1]}); vb.pb({b[i], b[n - i + 1]}); 39 } 40 sort(va.begin(), va.end()); 41 sort(vb.begin(), vb.end()); 42 for (int i = 0; i < n / 2; i++) { 43 if (va[i] != vb[i]) { 44 puts("No"); 45 return; 46 } 47 } 48 puts("Yes"); 49 } 50 51 int main() 52 { 53 //ios::sync_with_stdio(false); 54 cin >> T; 55 while (T--) { 56 solve(); 57 } 58 return 0; 59 }
------------------------------------------------------------------------------------------------------------
G是交互题，还没研究过交互题。=。=过段时间再补吧