Codeforces Round #645 (Div. 2) A~D题解

Codeforces Round #645 (Div. 2)

A.Park Lighting

 

 

题意：给出n*m的矩阵，要用一个能放置在两个方格之间的边来点亮两个方格的灯照亮所有方格。

题解：没什么好说的，直接上代码。

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 1, M = 1;
typedef long long ll;
typedef unsigned long long ull;
#define rep(i, x, y) for(i=x;i<=y;i++)
#define ref(i, x, y) for(i=x;i>=y;i--)
#define MEM(a, x) memset(a, x, sizeof(a))
#define Sca(x) scanf("%d", &x)
#define Scl(x) scanf("%lld", &x)
#define Scf(x) scanf("%f", &x)
#define Sclf(x) scanf("%lf", &x)

int T, n, m;
bool vis[N];

int main()
{
    cin >> T;
    while (T--) {
        cin >> n >> m;
        cout << (n * m + 1) / 2 << endl;
    }
    return 0;
}

B.Maria Breaks the Self-isolation

 

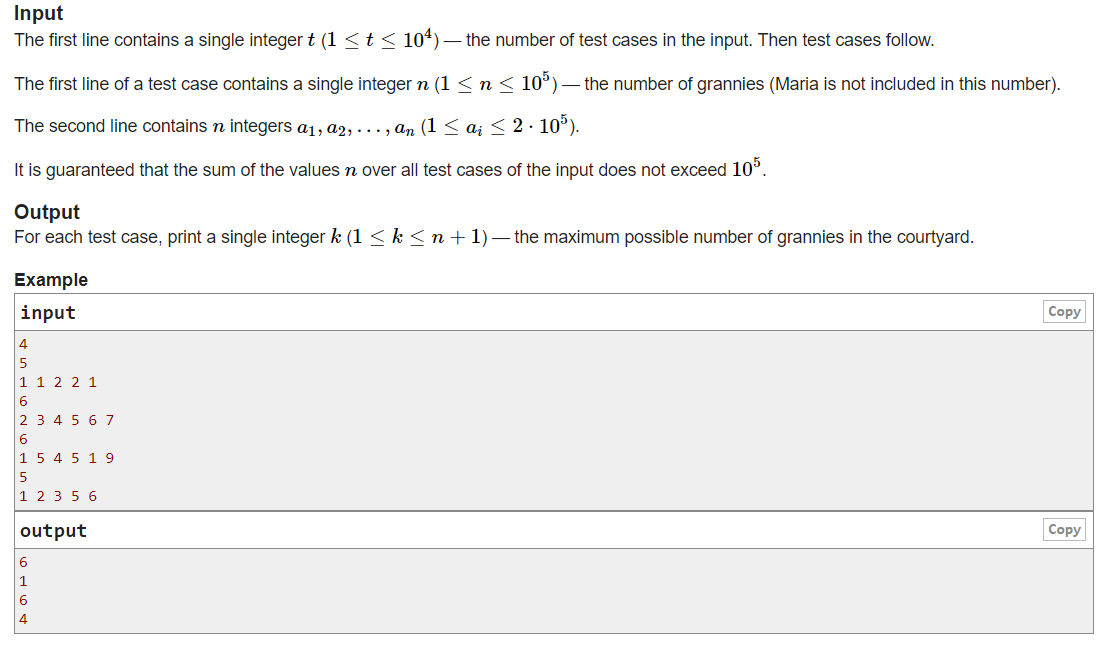
题意：建议大家提升英文水平（我忘了）

题解：直接上代码。

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+5, M = 1;
typedef long long ll;
typedef unsigned long long ull;
#define rep(i, x, y) for(i=x;i<=y;i++)
#define ref(i, x, y) for(i=x;i>=y;i--)
#define MEM(a, x) memset(a, x, sizeof(a))
#define Sca(x) scanf("%d", &x)
#define Scl(x) scanf("%lld", &x)
#define Scf(x) scanf("%f", &x)
#define Sclf(x) scanf("%lf", &x)

int T, n, a[N], cnt[N];
bool vis[N];

int main()
{
    cin >> T;
    while (T--) {
        cin >> n;
        for (int i = 1; i <= n; i++)
            Sca(a[i]);
        sort(a+1, a+1+n);
        int num = 0;
        for (int i = 1; i <= n; i++) {
            if (a[i] <= i) num = i;
        }
        cout << num + 1 << endl;
    }
    return 0;
}

 C.Celex Update

 

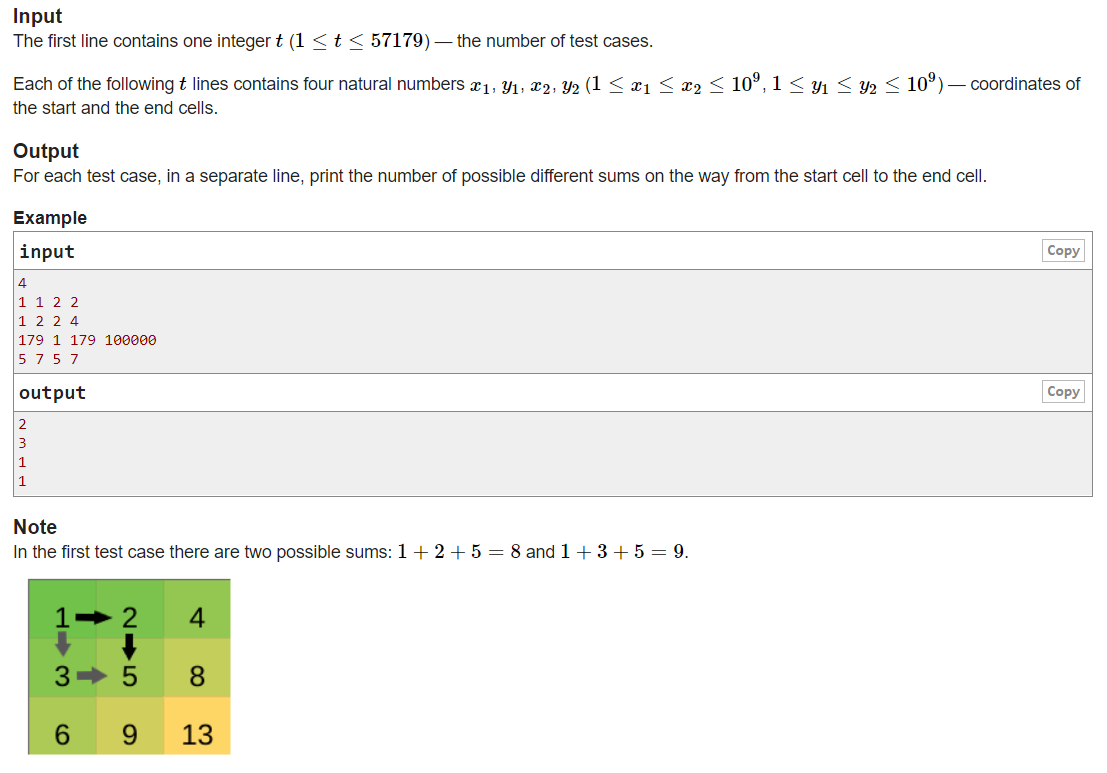
题意：给出两个点的坐标，求从第一个点走到第二个点（只能向下或向右），走时加上方格中的数字，求最后得到有多少种不同的数字和。

题解：首先，格子中的数字是斜向下增加1的。由此可知，走¬型的路线，得到的数字和是最小的，走L型的路线，得到的数字和是最大的。并且从一条路径的某一处本是向右改为向下，会使得数字和+1。于是由此，我们可以从最小的路线上的数字和+1一直加到最大路线和，也就是说，答案是最大-最小+1。于是我们可以将原图化为下面的形式：

则可以求得公式：　　ans=Δx∗Δy + 1

（当然也可以暴力然后找规律）

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 1, M = 1;
typedef long long ll;
typedef unsigned long long ull;
#define rep(i, x, y) for(i=x;i<=y;i++)
#define ref(i, x, y) for(i=x;i>=y;i--)
#define MEM(a, x) memset(a, x, sizeof(a))
#define Sca(x) scanf("%d", &x)
#define Scl(x) scanf("%lld", &x)
#define Scf(x) scanf("%f", &x)
#define Sclf(x) scanf("%lf", &x)

int T, n;
bool vis[N];

int main()
{
    cin >> T;
    while (T--) {
        int x1, x2, y1, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        ll x = x2 - x1, y = y2 - y1;
        ll ans = x * y + 1;
        cout << ans << endl;
    }
    return 0;
}

D.The Best Vacation

 

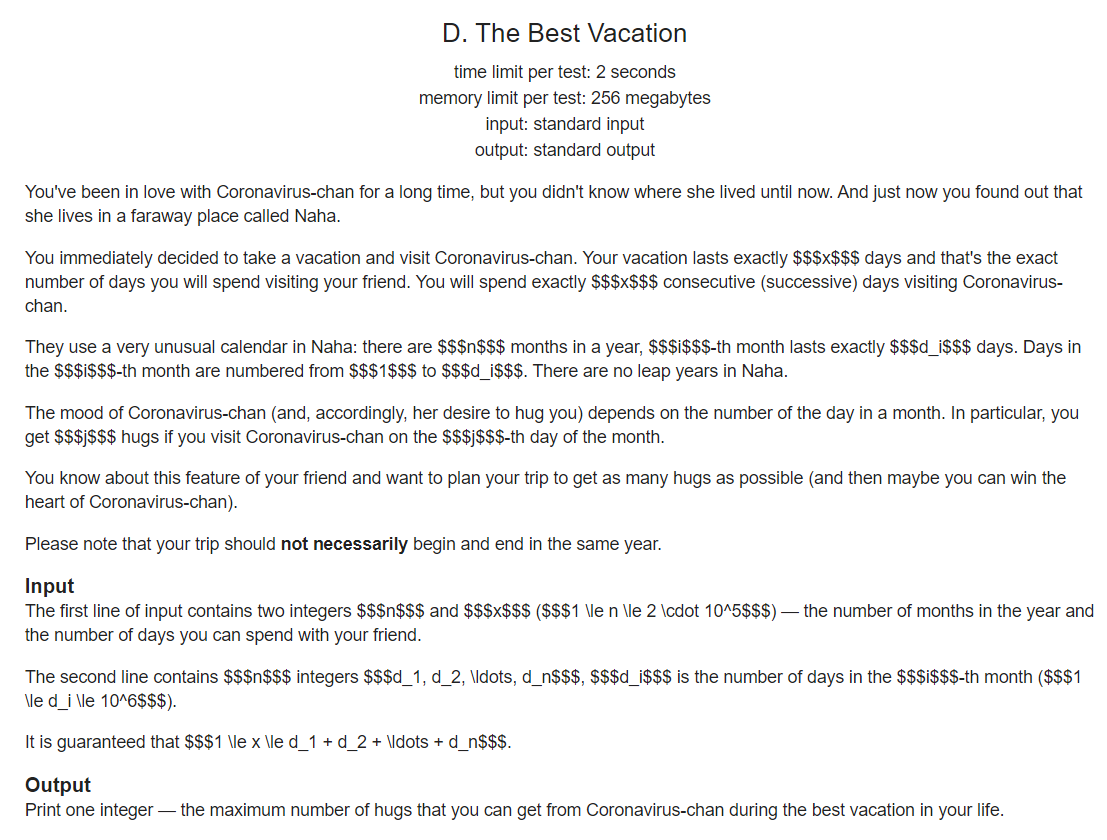
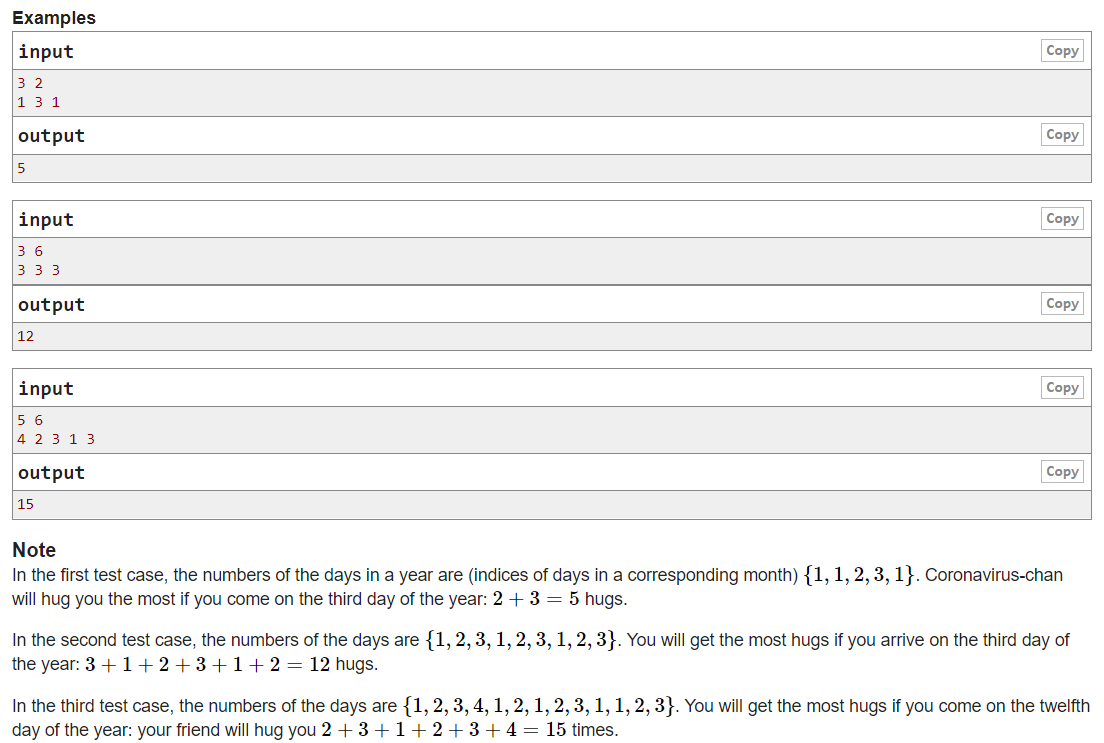
题意：不同的日月计法，一年有n个月，每个月ai天，每个月的第i天有i点幸福值，问在连续的k天中，能获得的最多的幸福值是多少。（可以不在同一年里）

题解：因为可以在不同的年中，所以我们可以在原本的n个月后再加上与原来一样的n个月，模拟成两年。然后思考，已经选取了连续的t个月，使得剩下的天数无论是在t个月的前一个月或是t个月的后一个月中，都无法完全覆盖整个月，这时选择向前去覆盖天数显然比向后去覆盖得到的幸福值要高。（CF上的题解好像有证明过程，如果我记得住会来补的）所以最优的策略一定是以某一个月结尾的。所以我们可以枚举2 *ｎ个月，以这个月为结尾的幸福值，然后取最大值即可。（用二分来寻找）

代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5+5, M = 1;
typedef long long ll;
typedef unsigned long long ull;
#define rep(i, x, y) for(i=x;i<=y;i++)
#define ref(i, x, y) for(i=x;i>=y;i--)
#define MEM(a, x) memset(a, x, sizeof(a))
#define Sca(x) scanf("%d", &x)
#define Scl(x) scanf("%lld", &x)
#define Scf(x) scanf("%f", &x)
#define Sclf(x) scanf("%lf", &x)
#define lb lower_bound

int T, d[N << 1];
ll SumDay[N << 1], SumNum[N << 1], n, x, ans;
bool vis[N];
ll calc(ll l, ll r)
{return (r - l + 1) * l + (r - l + 1) * (r - l) / 2;}

int main()
{
    cin >> n >> x;
    int mx = 0;
    for (int i = 1; i <= n; i++) {
        Sca(d[i]); SumDay[i] = SumDay[i - 1] + d[i]; SumNum[i] = SumNum[i - 1] + calc(1, d[i]);
    }
    for (int i = n + 1; i <= 2 * n; i++) {
        d[i] = d[i - n];
        SumDay[i] = SumDay[i - 1] + d[i - n]; SumNum[i] = SumNum[i - 1] + calc(1, d[i - n]);
    }
    for (int i = 2 * n; i >= 1; i--) {
        if (SumDay[i] < x) break;
        int l = 1, r = i;
        while (l < r) {
            int mid = l + r >> 1;
            if (SumDay[i] - SumDay[mid] - x <= 0) r = mid;
            else l = mid + 1;
        }
        // cout << "l = " << l << endl;
        ll temp = SumNum[i] - SumNum[l];
        ll sx = x - (SumDay[i] - SumDay[l]);
        if (sx) temp += calc(d[l] - sx + 1, d[l]);
        ans = max(ans, temp);
    }
    cout << ans << endl;
    return 0;
}